2. Поняття рангу системи векторів.

Нехай задано систему векторів довільного простору:

(1)

Означення. Максимальною лінійно незалежною підсистемою даної системи векторів називається така її лінійно незалежна підсистема приєднання до якої будь-якого вектора цієї ж системи приводить до лінійно залежної системи.

Означення. Рангом системи векторів (1) називається кількість векторів, що входить до максимальної лінійно-незалежної її підсистеми.

Зауваження Для того, щоб означення вимірності лінійного простору і означення рангу системи векторів було коректним, треба було б довести, що кількість векторів, що входять в будь-яку максимальну лінійно незалежну систему простору (а для рангу – будь-яку максимально-лінійно незалежної підсистеми) є однаковим.

Для подальшого потрібне таке означення.

Означення 1. Говоритимемо, що система векторів (1)лінійно виражається через систему векторів (2), якщо кожний вектор системи (1) є лінійною комбінацією векторів системи (2):

(3)

Означення 2. Системи векторів (1) і (2) називаються еквівалентними, якщо кожна з них лінійно виражається через другу

Властивість (транзитивності)

Якщо система векторів (1) лінійно виражається через систему векторів (2), а система (2) через систему (3), тоді система (1) лінійно виражається через (3).

Доведення.

Для зручності доведення цієї властивості введемо символ .

Нехай задано суму однотипних доданків

Застосовуючи двічі цей символ, отримаєм для

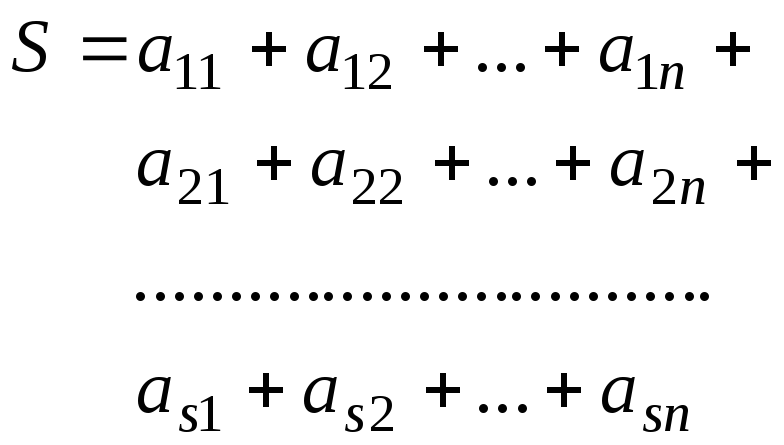
Доведемо таку властивість:

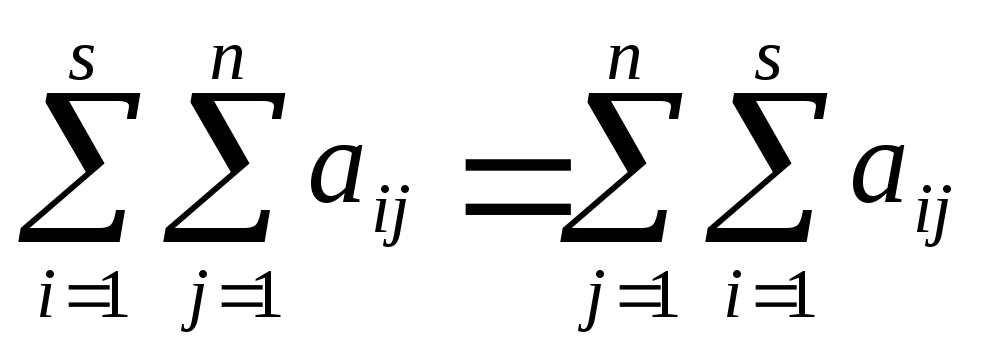
Для цього доведемо, що . Для доведення проведемо підсумування за стовпцями

_Отже

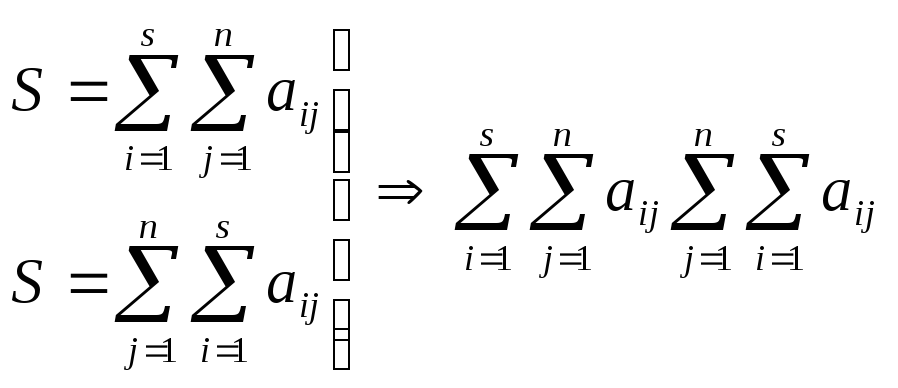
Тепер перейдемо до доведення попередньої властивості транзитивності.

Нехай задано системи:

(1)

(2)

(3)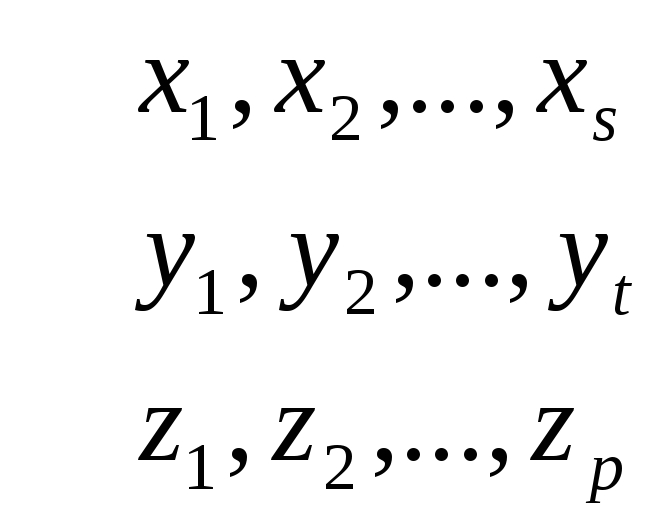

За умовою (1) лінійно виражається через (2). Тоді за означенням - є лінійною комбінацією векторів системи (2)

(i=1,2,…,S) (4)

За умовою (2) лінійно виражається через (3), тому

Підставимо (5) в(4), тоді отримаємо

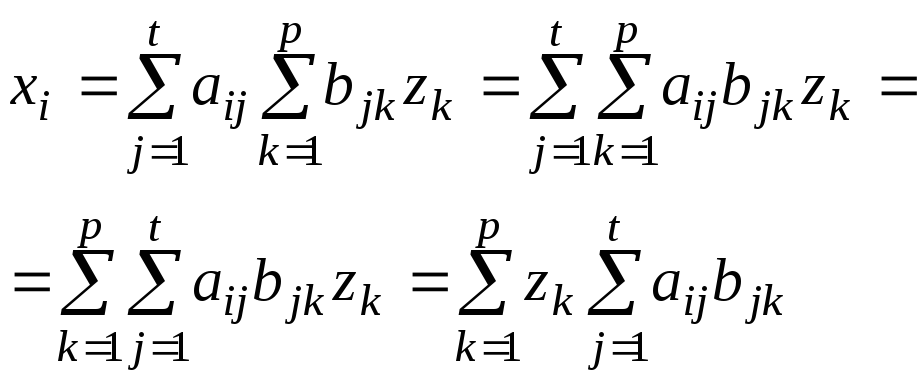
Отже доведено, що система векторів (1) лінійно виражається через систему (3).

Наслідок.Якщо система векторів (1) еквівалентна системі (2), а система (2) еквівалентна системі (3), то системи (1) і (3) еквівалентні.

Транзитивність еквівалентних систем доводиться повторенням двічі наведених міркувань.

3. Поняття рангу матриці. Теорема про ранг матриці.

Розглянемо довільну матрицю.

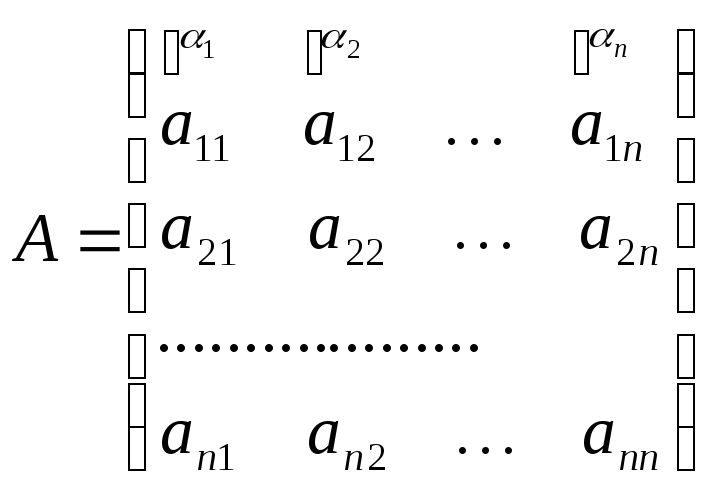
Кожний стовпець матриці можна розглядати як упорядковану -ку чисел, тобто матриця - це система п-векторів-вимірного арифметичного простору.

Використовуючи цю інтерпретацію і означення рангу системи векторів приходимо до доцільності такого означення.

Означення. Рангом матриці називається кількість стовпців, що входить до максимальної лінійно незалежної підсистеми стовпців матриць.

Або в скороченому вигляді можна дати таке формулювання.

Означення. Рангом матриці називається максимальна кількість лінійно-незалежних стовпців.

Теорема про ранг матриці. Найвищий порядок мінорів матриці, що не дорівнюють нулю, дорівнює рангу матриці.

Доведення.

Нехай найвищий порядок мінорів, що не дорівнюють нулю є число р. Це означає, що в матриці А є мінор р-того порядку, не рівний нулю. Мінори р + 1 і більш високих порядків дорівнюють нулю.

Для визначеності припустимо, що мінор р-того порядку не рівний нулю знаходиться в лівому верхньому куту.

М

Треба довести, що ранг матриці дорівнює р.

Для цього треба довести два факти:

1. в матриці А є р-лінійно-незалежних стовпців;

2. всі інші стовпці через них лінійно виражаються.

1) Доведемо, що лінійно незалежними (за нашим припущенням) є перші р стовпців матриці. Припустимо супротивне, що перші р стовпців матриці лінійно залежні. Тоді з означення лінійної залежності випливає, що існують числа , що виконується рівність:

Розглянемо цю рівність покомпонентно:

І компонента -

р компонента -

_{………………………………………………}

компонента -

З перших р рівностей випливає що стовпці мінора М - лінійно залежні. Доведемо, що тоді мінор М дорівнює нулю.

Розглянемо два випадки.

а)р = 1 тобто М =- лінійно залежний, а звідси випливає що.

б)р≥2 В цьому випадку лінійна залежність означає, що в мінорі М існує стовпець, що є лінійною комбінацією інших стовпців, а тоді за властивістю визначників мінор М = 0

Отже, ми прийшли до суперечності умові. Отже, перші р стовпців матриці А- лінійно незалежні.

Для доведення другого факту побудуємо визначник.

i=1,2,…,s

k=p+1,…n

Доведемо, що при всіх таких і та к визначник

Для доведення розглянемо два випадки:

1) . В цьому випадкуяк визначник з двома рівними рядками.

2) . В цьому випадку, бо визначникстає мінором р + 1 порядку матриці А, а тоді за умовою, він дорівнює нулю.

Розкладемо визначник за останнім рядком:

_.

Розв'яжемо цю рівність відносно _,

_.

Надамо всі значення

Це означає, що к- тий стовпець матриці А є лінійною комбінацією перших р-стовпців. Оскільки к набуває значень , то ми довели, що всі стовпці, починаючи з р + 1 є лінійними комбінаціями перших р- стовпців.

Що і треба було довести

Таким чином за означенням ранг дорівнює р.

Наслідки зтеореми про ранг:

Наслідок 1.

Максимальна кількість лінійно-незалежних рядків матриці дорівнює максимальному числу лінійно-незалежних стовпців матриці, тобто дорівнює рангу матриці.

Доведення:

Розглянемо довільну матрицю А

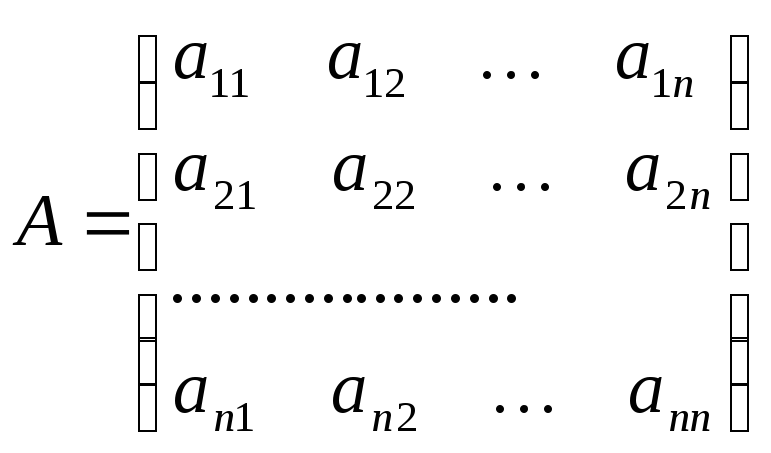
Нехай максимальна кількість лінійно-незалежних стовпців = р, тобто

Треба довести, що максимальна кількість лінійно-незалежних рядків = р.

Для доведення побудуємо транспоновану матрицю

1) Доведемо, що ранг матриці А' дорівнює р.

З того, що випливає (з теореми про ранг), що в матриці А є мінор р - того порядку, не рівний нулю,, а всі мінори більш високих порядків дорівнюють нулю.

Всі мінори матриці А в транспонованому вигляді знаходяться в матриці А'. Відомо, що при транспонуванні визначник не змінюється.

Тому в матриці А' є мінор р - того порядку не рівний нулю, а всі мінори більш високих порядків дорівнюють нулю. З теореми про ранг випливає, що

Тоді за означенням в матриці А' лише р лінійно незалежних стовпців, а вони є рядками матриці А

Наслідок 2.

Для того щоб визначник дорівнював нулю. Необхідно, щоб його рядки (стовпці) були лінійно залежними.

Доведення:

Нехай визначник . Треба довести, що його рядки (стовпці) лінійно-залежні

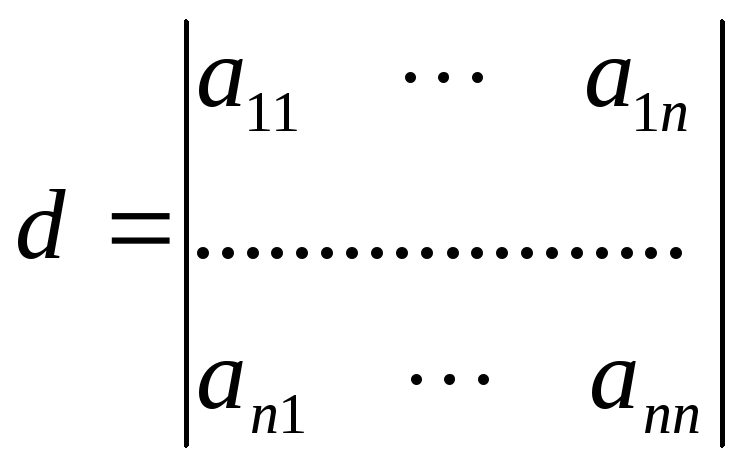
Розглянемо матрицю, що відповідає цьому визначнику

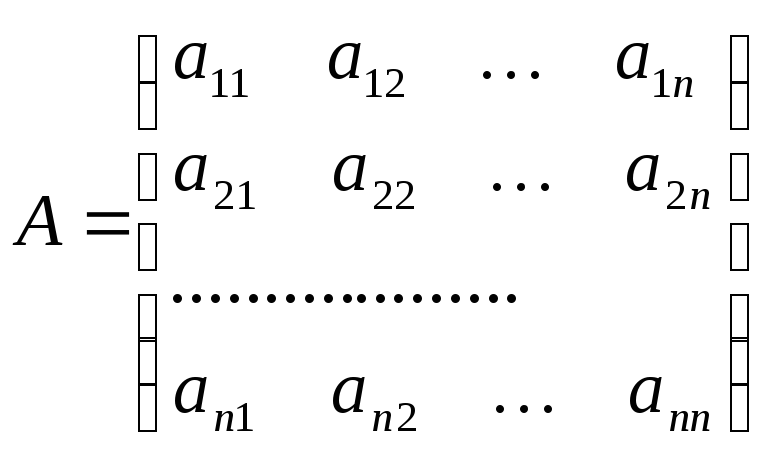
Доведемо, що

Припустимо супротивне, що , тоді з теореми про ранг випливає, що в А існує мінор d п - того порядку, не рівний нулю.

А за умовою . Ми отримали суперечність. Звідси випливає, що

Тоді за означенням рангу в матриці А лише р лінійно незалежних стовпців, інші n-р є їх лінійними комбінаціями.Тобто, загалом стовпці лінійно залежні.

Тепер ми можемо сформулювати необхідну і достатню умову рівності визначника нулю.

Теорема.

Для того, щоб визначник п - того порядку дорівнював нулю необхідно і достатньо, щоб його рядки (стовпці) утворювали лінійно залежну систему.

Доведення:

Необхідність:є другим наслідком теореми про ранг.

Достатність:

Нехай рядки (стовпці) лінійно залежні, треба довести, що .

При доведенні виникають два випадки.

1) Тоді-і його рядки лінійно-залежні

2) Тоді лінійна залежність рядків означає, що існує рядок, який є лінійною комбінацією інших.

А тоді за властивістю 9 визначників визначник дорівнює нулю.