МОДУЛЬ 1

I занятие

1.10. Два тела бросили одновременно из одной точки: одно — вертикально вверх, другое — под углом =60° к горизонту. Начальная скорость каждого тела v₀=25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через t=1,70 с.

1.21. В момент t=0 частица вышла из начала координат в положительном направлении оси х. Ее скорость меняется со временем по закону , где— начальная скорость, модуль которойv₀=10,0 см/с, =5,0 с. Найти:

1. координату х частицы в моменты времени 6,0, 10 и 20 с;

2. моменты времени, когда частица будет находиться на расстоянии 10,0 см от начала координат.

1.22. Частица движется в положительном направлении оси х так, что ее скорость меняется по закону , где  — положительная постоянная. Имея в виду, что в момент t=0 она находилась в точке x=0, найти:

1. зависимость от времени скорости и ускорения частицы;

2. среднюю скорость частицы за время, в течение которого она пройдет первые s метров пути.

1.23. Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости v по закону , где — положительная постоянная. В начальный момент скорость точки равна v₀. Какой путь она пройдет до остановки? За какое время этот путь будет пройден?

1.24. Радиус-вектор точки А относительно начала координат меняется со временем t по закону , где и  — постоянные, и— орты осейх и у. Найти:

1. уравнение траекторий точки у(х); изобразить ее график;

2. зависимости от времени скорости , ускоренияи модулей этих величин;

3. зависимость от времени угла  между векторами и.

1.25. Точка движется в плоскости ху по закону x= t, , где и  — положительные постоянные. Найти:

1. уравнение траектории точки у(х); изобразить ее график;

2. скорость v и ускорение а точки в зависимости от t;

3. момент t₀, когда угол между скоростью и ускорением равен /4.

1.26. Точка движется в плоскости ху по закону ,, гдеА и  — положительные постоянные. Найти:

1. путь s, проходимый точкой за время ;

2. угол между скоростью и ускорением точки.

1.37. Точка движется по окружности со скоростью v= t, где =0,50 м/с². Найти ее полное ускорение в момент, когда она пройдет n=0,10 длины окружности после начала движения.

II занятие

1.39. Точка движется по дуге окружности радиуса R. Ее скорость зависит от пройденного пути s по закону , где — постоянная. Найти угол  между вектором полного ускорения и вектором скорости в зависимости от s.

1.40. Частица движется но дуге окружности радиуса R по закону l=A sin  t, где l — смещение из начального положения, отсчитываемое вдоль дуги, A и  — постоянные. Положив R=1,00 м, A=0,80 м и =2,00 с^-1, найти полное ускорение частицы в точках l=0 и ±A.

1.44. Колесо вращается вокруг неподвижной оси так, что угол  его поворота зависит от времени как = t², где =0,20 рад/с². Найти полное ускорение а точки А на ободе колеса в момент t=2,5 с, если скорость точки А в этот момент v=0,65 м/с.

1.45. Снаряд вылетел со скоростью v=320 м/с, сделав внутри ствола n=2,0 оборота. Длина ствола l=2,0 м. Считая движение снаряда в стволе равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета.

1.46. Твердое тело вращается вокруг неподвижной оси по закону  =at–bt³, где a=6,0 рад/с, b=2,0 рад/с³. Найти:

1. средние значения угловой скорости и углового ускорения за промежуток времени от t=0 до остановки;

2. угловое ускорение в момент остановки тела.

1.47. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением  = t, где  =2,010^–2 рад/с³. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол  =60° с ее вектором скорости?

1.48. Твердое тело вращается, замедляясь, вокруг неподвижной оси с угловым ускорением , где — его угловая скорость. Найти среднюю угловую скорость тела за время, в течение которого оно будет вращаться, если в начальный момент его угловая скорость была равна ₀.

1.49. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота  по закону =₀–a, где ₀ и а— положительные постоянные. В момент времени t=0 угол  =0. Найти зависимости от времени:

1. угла поворота;

2. угловой скорости.

1.50. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением , где— постоянный вектор,  — угол поворота из начального положения. Найти угловую скорость тела в зависимости от угла . Изобразить график этой зависимости.

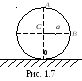
1.53. Шар радиуса R=10,0 см катится без скольжения по горизонтальной плоскости так, что его центр движется с постоянным ускорением а=2,50 см/с². Через t=2,00 с после начала движения его положение соответствует рис. 1.7. Найти:

а) скорости точек А и В;

b) ускорения точек A и O.

1.56. Твердое тело вращается с угловой скоростью ω=ati+bt²j, где a=0,50 рад/с², b=0,060 рад/с³, i и j — орты осей х и у. Найти модули угловой скорости и углового ускорения в момент t=10,0 с.