I. Представление некоторых функций формулой Маклорена ():
а) 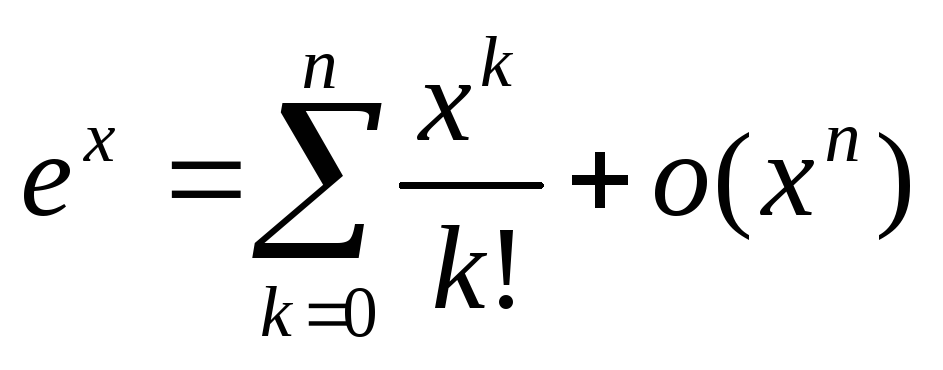 , б)
, б)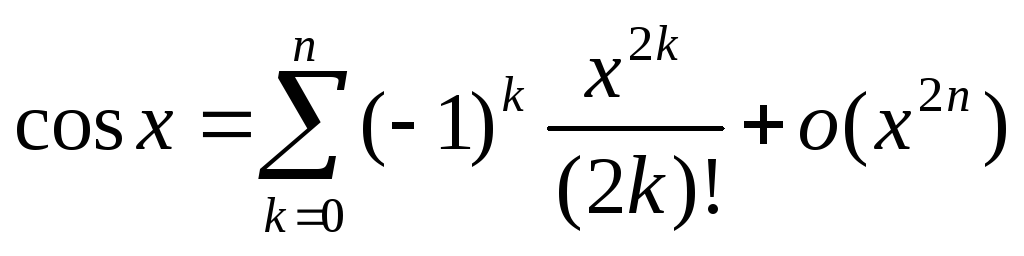 ,
,
в) 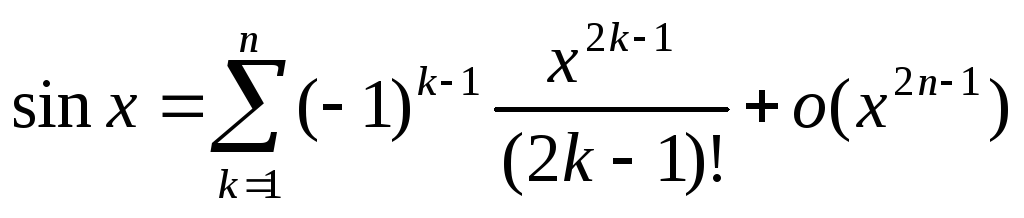 , г)
, г)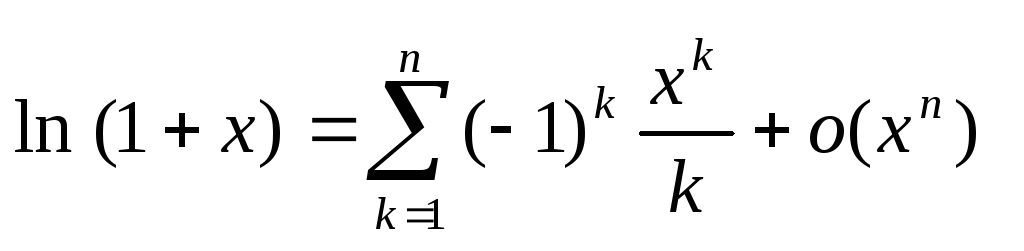 ,
,
д) 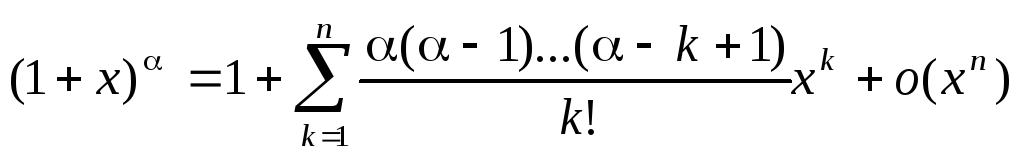 .
.
Доказательство
сразу вытекает из соотношений:
а) 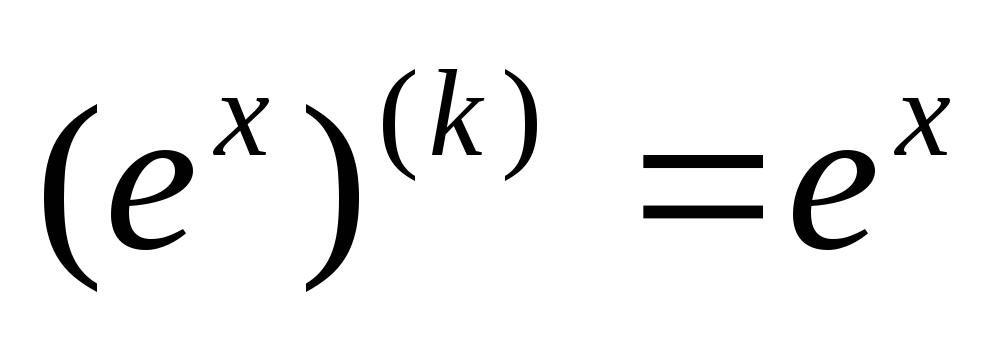 , б)
, б)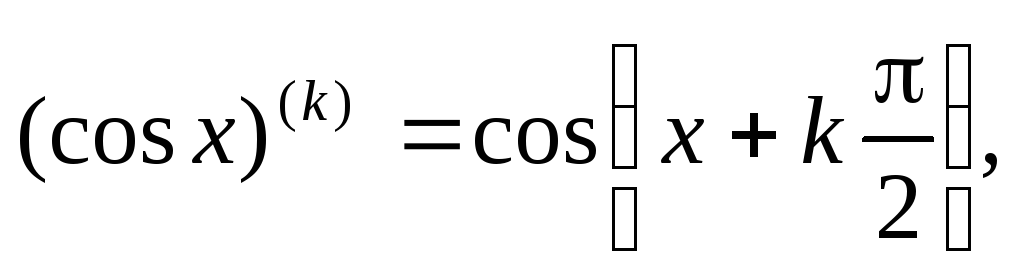 в)
в)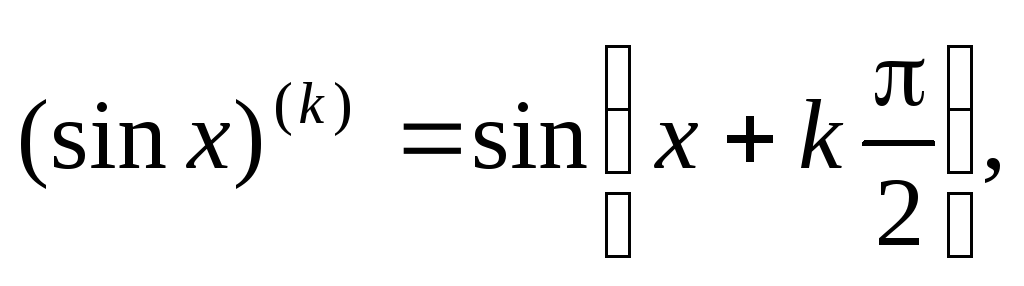
г) 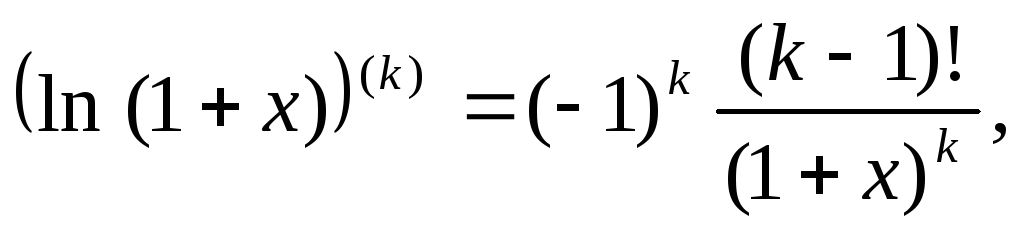 д)
д)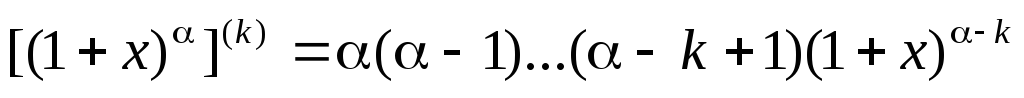 .
.
Вставка 4.
II. Третье
достаточное условие локального
экстремума. Пусть дана функция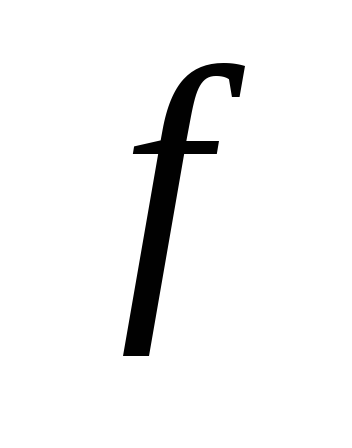 .
Если из производных, не обращающихся в
нуль в точке
.
Если из производных, не обращающихся в
нуль в точке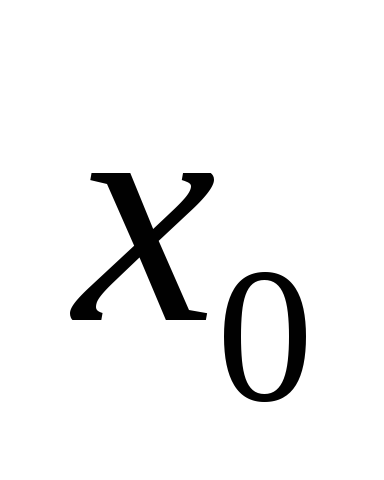 ,
первой оказывается производная нечетного
порядка, то
,
первой оказывается производная нечетного
порядка, то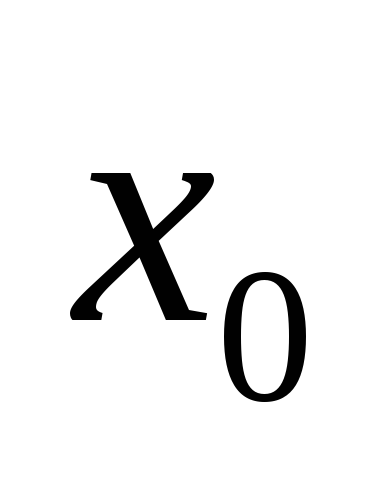 не является точкой локального экстремума.
Если же такой производной является
производная четного порядка, то
не является точкой локального экстремума.
Если же такой производной является
производная четного порядка, то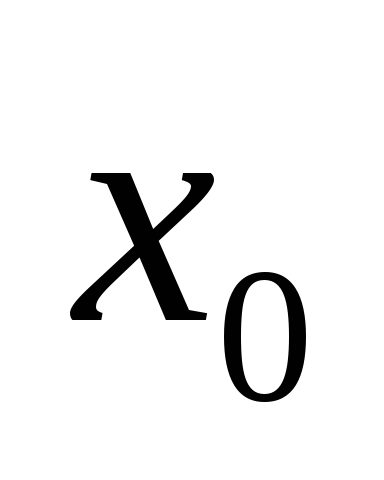 - точка локального экстремума, причем
точкой максимума, если эта производная
отрицательна, и минимума, если эта
производная положительна.
- точка локального экстремума, причем
точкой максимума, если эта производная
отрицательна, и минимума, если эта
производная положительна.
Действительно, пусть
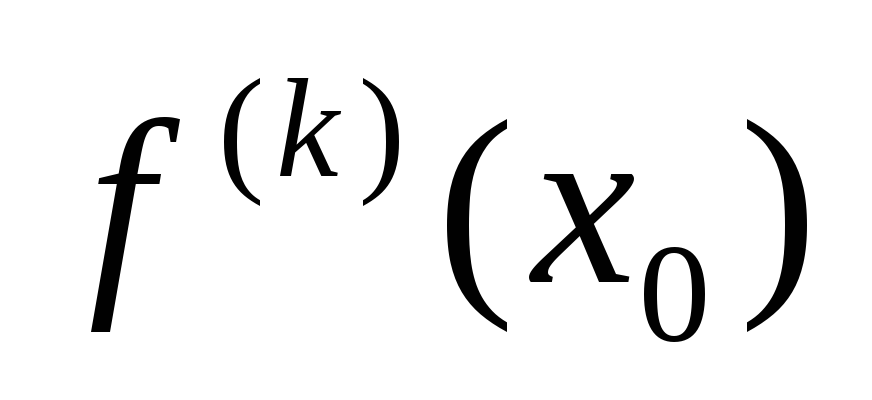 ,
,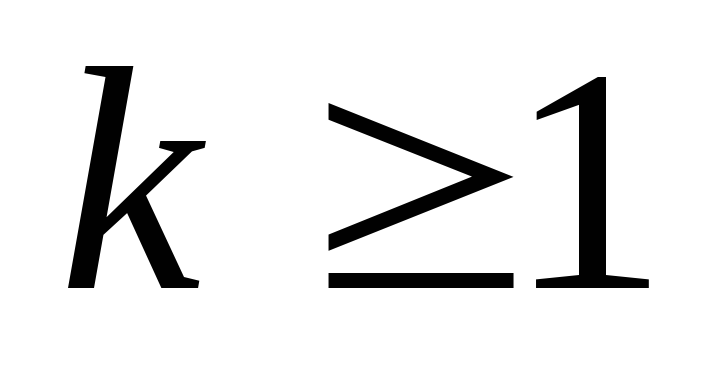 ,
- первая производная, отличная от нуля.
Запишем формулу Тейлора в следующем
виде
,
- первая производная, отличная от нуля.
Запишем формулу Тейлора в следующем
виде
 при
при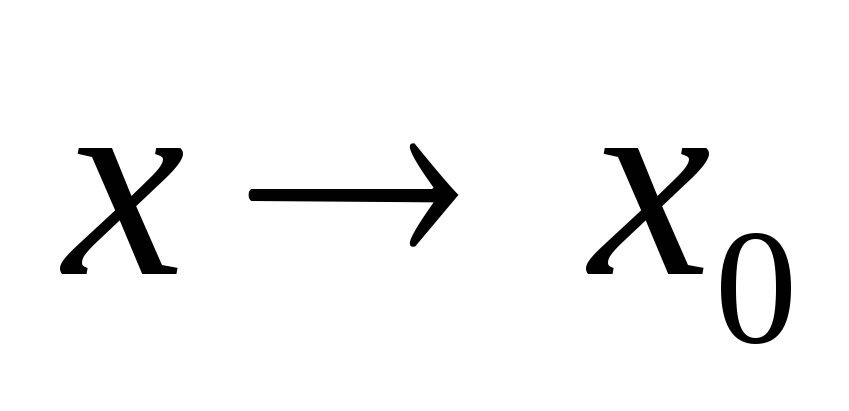 .
.
Ясно, что при х,близких кх0,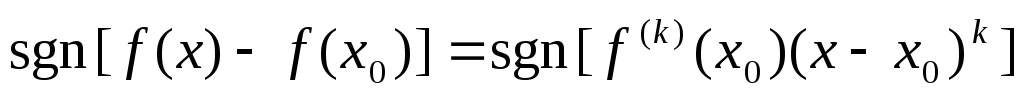 .
Поэтому при нечетном
.
Поэтому при нечетном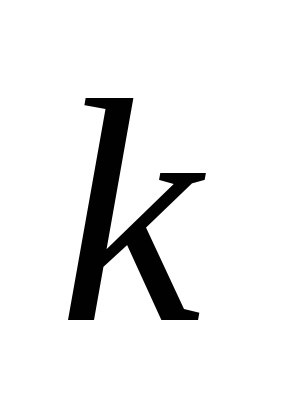 этот знак меняется в зависимости от
полуокрестности, и потому экстремума
в точке
этот знак меняется в зависимости от
полуокрестности, и потому экстремума
в точке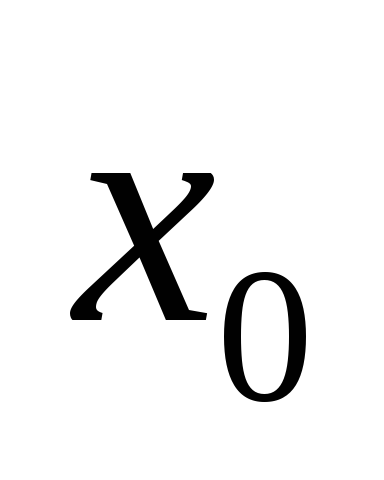 нет. При четном
нет. При четном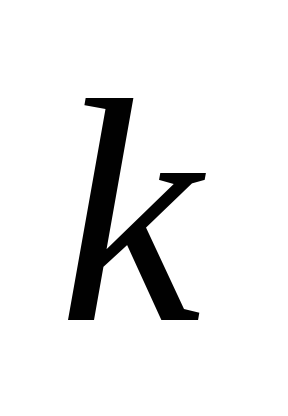 знак не меняется, что и означает наличие
экстремума в точке
знак не меняется, что и означает наличие
экстремума в точке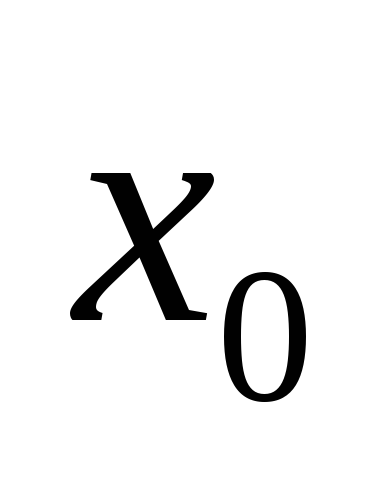 .
.
Вставка 5.
III. Приближенные
вычисления. При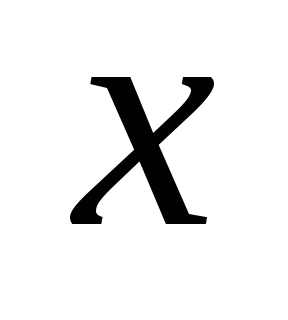 ,
близком к
,
близком к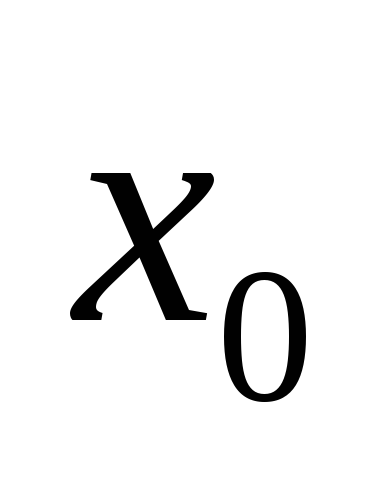 ,
из формулы Тейлора получим формулу для
приближенных вычислений значения
функции
,
из формулы Тейлора получим формулу для
приближенных вычислений значения
функции
 ,
,
причем за счет увеличения числа
 можно будет добиться наперед заданной
точности вычислений (об этом более
подробно будет изложено во второй части
в теме «Ряды»).
можно будет добиться наперед заданной
точности вычислений (об этом более
подробно будет изложено во второй части
в теме «Ряды»).
Вставка 6.
IV..
Выделение главной части функции.Из формулы Тейлора следует, что главная
часть функцииf при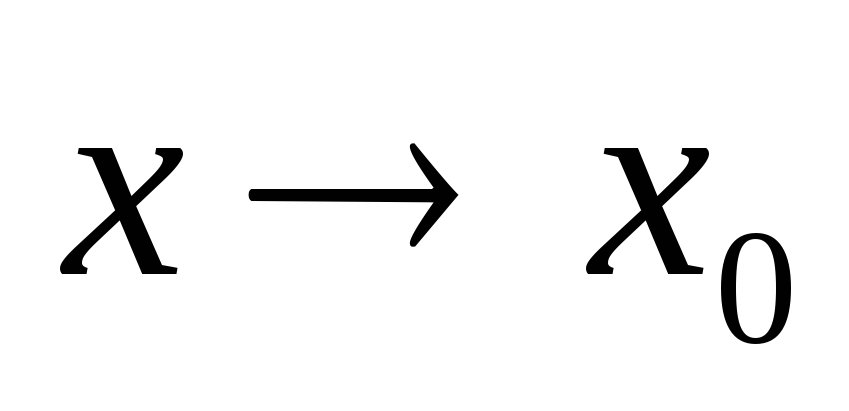 равна, например, первому слагаемому
равна, например, первому слагаемому ,
отличному от нуля.
,
отличному от нуля.
Вставка 7.
Y.Вычисление
пределов основано на формуле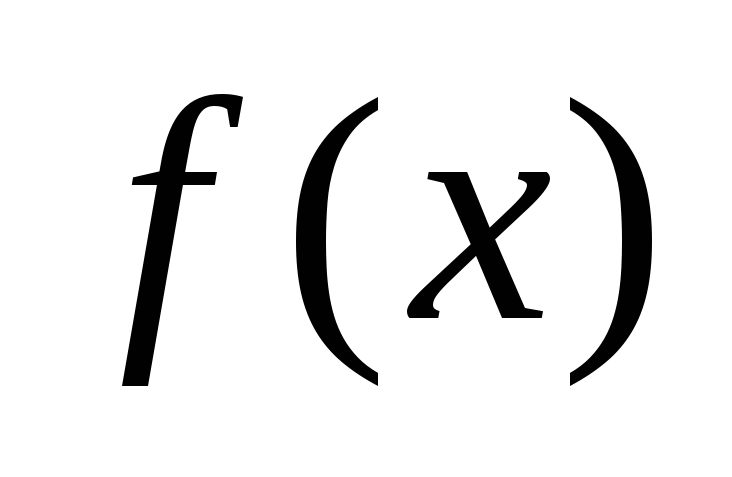 ~
~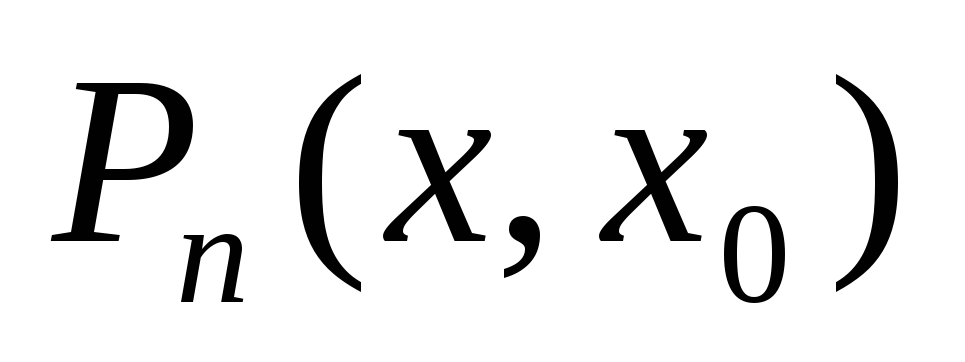 при
при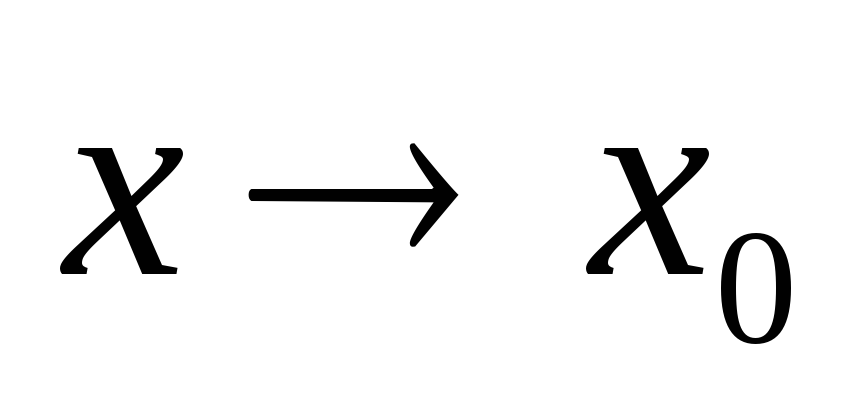 ,
где
,
где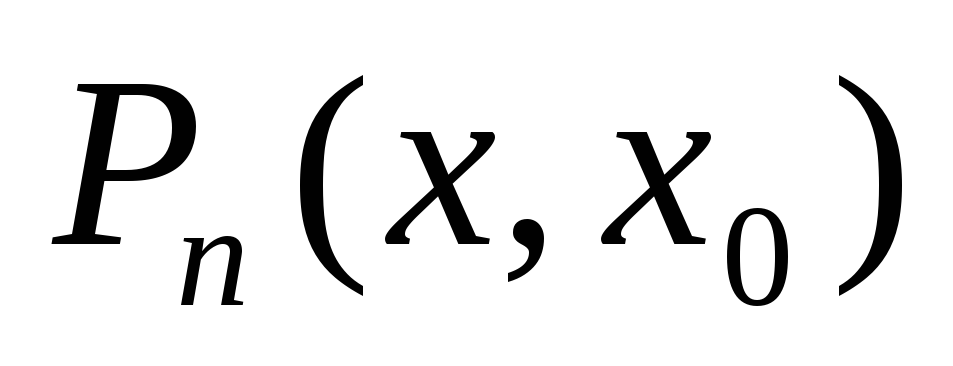 - многочлен Тейлора, что равносильно
замене функции fее главной частью при
- многочлен Тейлора, что равносильно
замене функции fее главной частью при .
.
Вставка 8.
Вопросы и упражнения
1. Доказать формулу
бинома Ньютона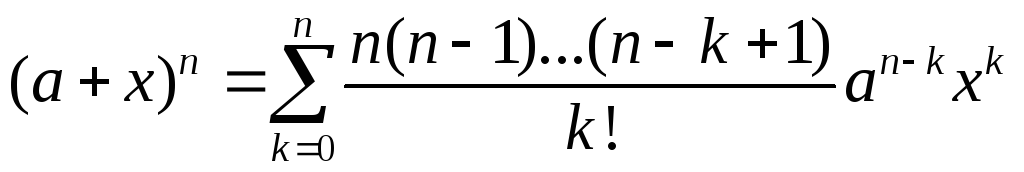 .
.
2.Доказать, что формула Маклорена
для четной (нечетной) функции содержит
только четные (нечетные) степени.
76

