§ 5. Правило Лопиталя

Теорема1 (раскрытие неопределенности). Пусть функцииинепрерывны и дифференцируемы в, причемив, иТогда, если существует предел ( конечный или бесконечный)

, (1)

то существует равный ему предел

. (2)

Доказательство. 1) Пусть сначала. Доопределим функцииив точкепо непрерывности, полагая,. Тогда к функциямиприменима теорема Коши:, лежащая междуитакая, что

. (3)

Так как при точка, то из (1) вытекает, что, а потому из (3) получим (2).

2) Пусть теперь . Сделаем замену. Тогда получим функциии. Они непрерывны и дифференцируемы в некоторой, причемив. Действительно,,. Поэтому, если, то

.

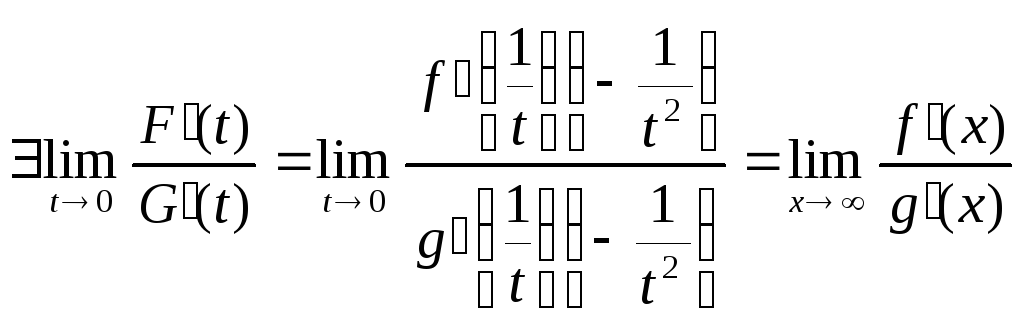На основании уже доказанного в 1) имеем окончательно

.

Вставка 1.

Существенно труднее доказывается следующая теорема, которую примем без доказательства.

Теорема2 (раскрытие неопределенностиПусть функцииинепрерывны и дифференцируемы в,ви. Тогда, если( конечный или бесконечный ), то.

Вставка 2.

Вопросы и упражнения

1. Справедливы ли теоремы 1 и 2 для односторонних пределов? Ответ обосновать.

2. Показать, что существование наклонной касательной y = Ax + B к графику дифференцируемой в соответствующей точке функции равносильно условиям: ,.

3. Какие условия надо добавить в теореме 2, чтобы прошло следующее ее доказательство?

. Тогда ,

откуда

, а значит, и .

§ 6. Формулы Тейлора и Маклорена и некоторые их применения

Пусть P_n(x) – многочлен степениn. Если функциядифференцируема в точке, то, как было показано (гл.Y, § 1),ее можно представить в видепри. Поставим более общую задачу. Пусть функцияимеет в точкепроизводных. Требуется выяснить, существуют ли многочленытакие, чтопри, и если да, то сколько их.

Теорема1 (формула Тейлора с остаточным членом в форме Пеано). Пусть функцияраз дифференцируема в. Тогда приимеет место равенство

,. (1)

Доказательство. Положим. Поскольку, то.

Поэтому, применяя раз правило Лопиталя, получим

, откуда

=при, т.е. получили (1).

Определение. Многочленназываетсямногочленом Тейлорав окрестности точки, а приназываетсямногочленом Маклорена, формула (1) называется -формулой Тейлора, а - остаточным членом в форме Пеано.

Вставка 1.

Теорема2 (единственность разложения функции по формуле Тейлора). Пусть функцияnраз дифференцируема випри.

Тогда , т.е. представление в данном виде единственно.

Доказательство. Из условия теоремы и формулы Тейлора получим равенство

=.

Переходя здесь к пределу при , будем иметьЕсли теперь в предыдущем равенстве привести подобныеи, сократить полученный результат наи вновь перейти к пределу при, то получим. Продолжая этот процесс, получим утверждение теоремы.

Вставка 2.

Теорема3 (формула Тейлора с остаточным членом в форме Лагранжа). Пусть функцияраз дифференцируема в. Тогда найдется точка, лежащая междуитакая, что

.

Доказательство. Рассмотрим функцию. Тогда, как показано в теореме 1, выполнены равенства. Положим. Для этой функции также имеем равенства. Поэтому, применяяраз теорему Коши (§ 1), получим, что, лежащие междуи(приполагаем=) такие, что

.

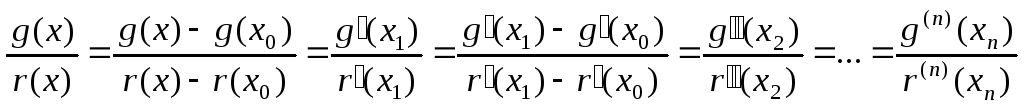Применим еще раз теорему Коши: найдется точка , лежащая междуиx_n , а значит, лежащая междуитакая, что

.

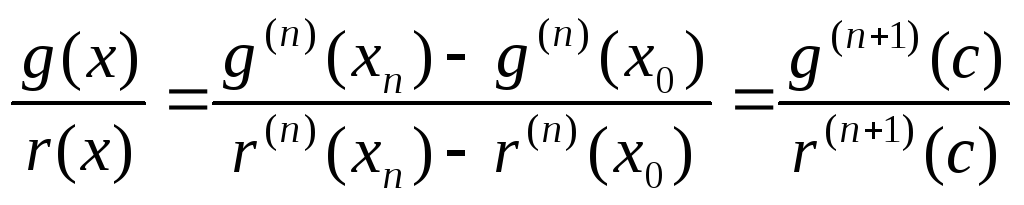Отсюда окончательно имеем

,

что и требовалось доказать.

Вставка 3.

Рассмотрим некоторые приложения формулы Тейлора.