Приклади розв'язання декотрих задач, поданих в посібнику.

В даному розділі наведені приклади розв'язання декотрих задач, що подані у відповідних розділах посібника а також інших задач, розв'язання яких має практичну користь для розуміння матеріалу. У більшості задач наведені шляхи розв'язку не є єдино можливими.

Перед розв'язком задач, умови яких не описані у відповідних розділах посібника, наводиться їх умова.

Кейнсіанська модель макрорівноваги. Задача №2.

Функція споживання, за умовами задачі, дорівнює . В кейнсіанській моделі, функція споживання має вигляд. Співставивши ці дві формули, ми з'ясовуємо, що в нашій задачі:С = 150 і c'(гранична схильність до споживання) = 0,5.

а)Функція загальних витрат AD за кейнсіанською моделлю має вигляд:

, і.

Тобто . Підставимо дані з умови задачі в цю формулу. Отримаємо:AD = 150 + 0,5 (Y-80) + 125 + 75 = 310 + 0,5Y.

Отже, AD = 310 + 0,5Y.

б) Для того, щоб розрахувати рівноважний доход (AD=Y), прирівняймо отриману нами в пункті а) формулу AD до Y.

Y = 310 + 0,5Y  Y - 0,5Y = 310  AD = Y = 620

в) Мультиплікатор, що визначає залежність між зміною податків і рівноважного доходу обраховується за формулою: . Підставимо значенняc' = 0,5 в цю формулу, отримаємо: .

Отже, якщо податки зменшаться на 5 одиниць (), то зміна рівноважного доходу (випуску) становитиме: , тобтовипуск зросте на 5 одиниць.

Задача №3

Відповідно до умов задачі, маємо, що гранична схильність до споживання c' = 0,75, а частка податків у доході t = 30% = 0,3.

Мультиплікатор, що визначає залежність між зміною державних витрат і сукупного випуску обраховується за формулою: і в нашому випадку дорівнюватиме:.

Тоді, якщо державні витрати збільшаться на 80 одиниць (G=80), то приріст сукупного випуску становитиме: , тобтовипуск зросте на 168, 424 одиниці.

Задача №4

Для визначення рівня запланованих витрат (попиту) AD підставимо значення Y=640 в формулу: AD = 310 + 0,5Y = 310 + 0,5640 = 630. Отже, виходить, що обсяг виробництва більший за попит на 10 одиниць, які будуть віднесені до запасів (запаси збільшаться). При цьому обсяг виробництва буде скорочуватись, поки не досягне рівноважного рівня, який становить:

Y = AD = 310 + 0,5Y  Y – 0,5Y = 310  AD = Y = 620.

Модель is-lm (рівновага товарного і грошового ринку). Додаткова задача №1

Нехай маємо закриту економіку, що описується такою системою рівнянь:

- основна макроекономічна тотожність;

- функція споживання;

- податки;

- інвестиційна функція;

- державні витрати;

- функція попиту на гроші;

- пропозиція грошей;

- рівень цін.

Необхідно: а) вивести рівняння кривої IS та кривої LM.

б) визначити рівноважну процентну ставку r та рівень доходу Y;

в) вивести рівняння кривої сукупного попиту і побудувати її графік, виходячи з того, що ціни зросли до рівня

Розв'язок.

а) Виведемо рівняння кривої LM.

В загальному випадку, крива LM, як залежність між відсотковою ставкою r та випуском Y, що характеризує рівновагу на грошовому ринку, задається так:

З рівняння попиту на гроші, ми отримуємо, що k=0,75, h=6, а .

Тоді рівняння кривої LM прийме вигляд:

Тепер виведемо рівняння кривої IS.

Вона має такий загальний вигляд:

Із умов задачі та із рівняння С (споживання) знайдемо, що =170,c'=0,6, T=200, G=350, I=100-4r.

Тоді рівняння кривої IS прийме вигляд:

.

б) Для того, щоб визначити рівноважні процентну ставку та рівень доходу нам необхідно знайти точку перетину кривих IS та LM. Для цього розв'яжемо систему:

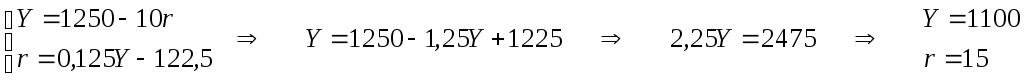
Таким чином, рівноважна процентна ставка становить 15%, а рівноважний доход – 1100.

в) Пряма сукупного попиту виражає залежність між запланованими витратами (AD) і рівнем виробництва Y (пропозицією). В загальному вона має вигляд: ,де , а .

Таким чином: . Невідомим в даному виразі є лише r (відсоткова ставка), визначити яку ми можемо із рівнянь грошового попиту та даних про грошову пропозицію, прирівнявши попит до пропозиції:

В нашому прикладі рівень цін p дорівнює 2, отже:

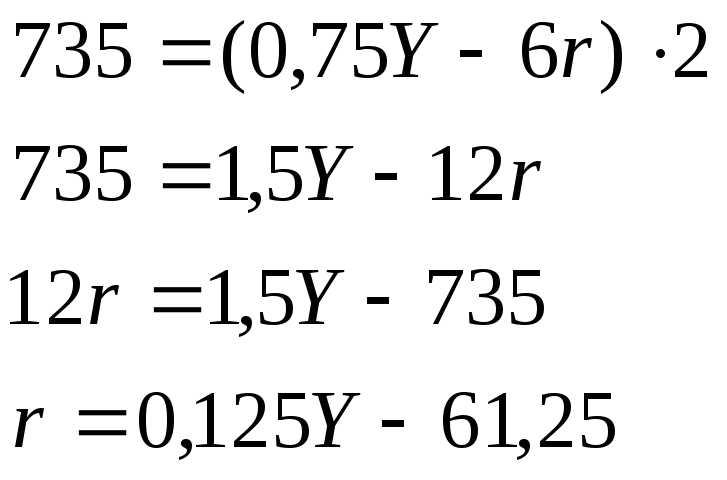
Підставимо отриманий вираз в рівняння сукупного попиту:

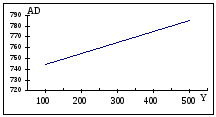
Її графік має такий вигляд: