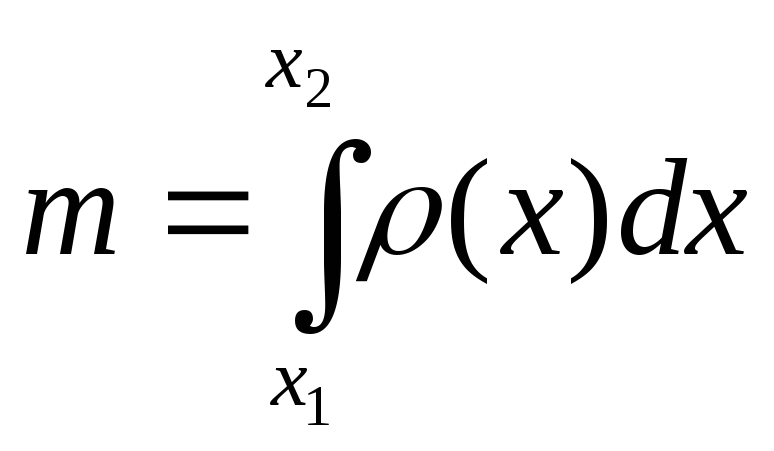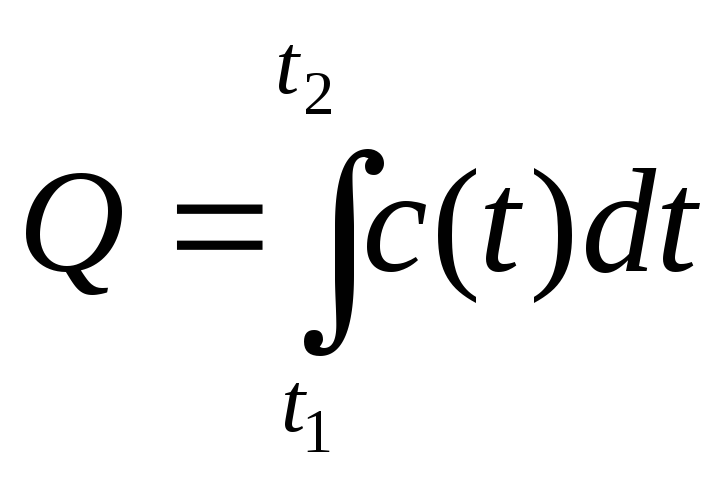Застосування інтеграла у фізиці та економіці.

План.

1. Обчислення шляху за відомим законом зміни швидкості.

2. Обчислення роботи змінної сили.

3. Обчислення маси неоднорідного стержня.

4. Обчислення кількості електрики.

5. Застосування інтеграла в економіці і техніці.

Рекомендована література.

Алгебра і початки аналізу: Підруч.для 10-11 кл.загальноосвіт.навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С.Дубинчук – К.: Зодіак-ЕКО, 2000.-608с.

Розділ 9.§ 4, п.4.

Дайте письмові відповіді на запитання.

Запишіть формули:

1. Обчислення шляху за відомим законом зміни швидкості.

2. Обчислення роботи змінної сили.

3. Обчислення маси неоднорідного стержня.

4. Обчислення кількості електрики.

5. Застосування інтеграла в економіці і техніці.

№ пп	Величини	Співвідношення	Знаходження похідної	Знаходження інтеграла
1	S – переміщення v -- швидкість
2	A - робота F - сила
3	A - робота N - потужність
4	m– маса тонкого стержня - лінійна густина
5	q– електричний заряд I – сила струму
6	Q – кількість теплоти c- теплоємність

Задача 1

При якій висоті рідини в циліндричній посудині радіусом сила тиску на дно посудини та на бічну стінку будуть однаковими?

Розв’язання

Тиск рідини на стінки посудини Р= ρgһ, відповідно, сила тиску дорівнює . Тиск на бічну стінку залежить від глибини у: Р(y) = ρgy. Розіб’ємо подумки бічну стінку на кільцеві смужки висотою dy, тоді сила тиску смужки на глибині dF(y)= ρgy2πrdy. Повна сила знаходиться інтегруванням по всім кільцям:

F₂ = dF(y) = ρg2πr ydy = πρgrһ² .

З умови F₁ = F₂ отримуємо = r.

Задача 2

До стелі ліфта, що вільно падає, прикріплено пружину з важком. Важок не коливається. Знайти максимальне значення сили пружності при миттєвій зупинці ліфта, якщо безпосередньо перед зупинкою ліфта сума потенціальної енергії важка дорівнювала 40 Дж. Коефіцієнт жорсткості пружини 500 Н/м. Тертям та масою пружини знехтувати. Потенціальну енергію сили пружності і сили тяжіння відраховувати від положення максимального розтягу пружини.

Розв’язання

Згідно формули для роботи рівнодійної сили Е_k - Е_k0 = А_mg – А_пружн

Так, як А_mg = mgx_max =Е_п0, тобто, початковій потенціальній енергії важка, а

А_пружн = = = .

Тоді маємо -Е_k0 = Е_п0 - ,

тобто повна енергія

Е_повн = Е_k0 + Е_п0 = . звідки

F_пружн = 200 Н

Задача 3

Температура маси m ідеального газу з молярною масою М змінюється за законом Т = αV², де α – відома стала. Яку роботу виконує газ при збільшенні його об’єму від V₁ до V₂? Чому дорівнює зміна внутрішньої енергії газу в цьому процесі? Отримує чи віддає газ тепло в цьому процесі?

Розв’язання

Скористаємось рівнянням стану ідеального газу:

Роботу можна знайти методом інтегрування:

Для визначення внутрішньої енергії скористаємось формулою

,

Отже,

Згідно першого закону термодинаміки , теплота, надана тілу в цьому процесі, дорівнює д

> 0,

отже газ отримує теплоту.

Задача 4

Над ν = 2 молями ідеального газу здійснюється цикл 1234(див рис),

Який складається із двох ізобар(12, при тиску Р₁=100 кПа, та 34, при тиску Р₃=272 кПа) та двох ізотерм (23, при температурі Т₂= 700 К, та 41, при температурі Т₁= 300 К).Знайти теплоту, яку газ поглинає за цикл.

Розв’язання

Згідно першого закону термодинаміки, Q = ∆U +А. В коловому процесі зміна внутрішньої енергії дорівнює нулю, отже Q = А. на ізобарах 12 і 34 робота дорівнює

А₁₂ = Р₁ (V₂ - V₁), А₃₄ = Р₃ (V₄ - V₃),

або враховуючи рівняння стану в точках 1234

Р₁V₁ = Р₃V₄ = νRT_1,

Р₁V₂ = Р₃V₃ = νRT₂

отримуємо А_{12 +} А₃₄ = 0

Аналогічно,

,

Отже,

< 0

Підстановка даних із умови задачі дає Q = -3,32 кДж, теплота віддається, а не поглинається, тобто , в цьому циклі теплова машина працює як холодильник.