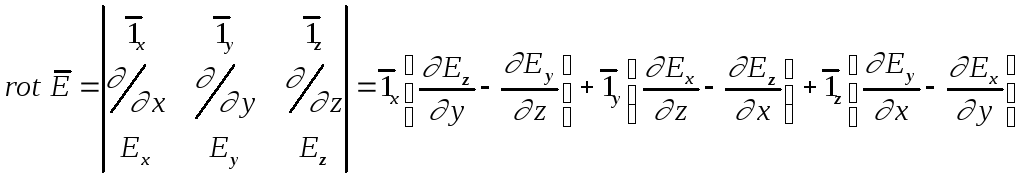2.5. Четвертое уравнение Максвелла.
Так как в природе не обнаружено магнитных зарядов и токов, то закон Гаусса и его дифференциальная форма в этом случае описываются следующим образом:
.
Векторное поле магнитной индукции не имеет стоков и истоков. Силовые линии замкнуты. Поле соленоидальное.
2.6. Первое уравнение Максвелла.
,
выделим некоторый замкнутый контур V
и поверхность S, которая опирается на
этот контур. Введем положительную
единичную нормаль к поверхности S.
Для того, чтобы
определить поле вектора 
необходимо воспользоваться законом
Ампера или законом полного тока.
Положительное направление обхода контура и единичной нормали связаны правилом правого винта. Напряженность магнитного поля можно определить, используя закон полного тока:
(1).
Запишем правую часть в интегральной форме:
(2).
Левую часть
преобразуем по теореме Стокса (поверхность
S произвольная): 
.
(3)
Соотношение (3)
называется дифференциальной
формой закона полного тока для
стационарного процесса. Возьмем
дивергенцию левой и правой частей 
:
(4).
Будем рассматривать
случай переменного (нестационарный
процесс) тока. Должно выполняться
соотношение: 
.
Однако выполнялось соотношение (4).
Максвелл добавил некую величину
и получил: 
;
(4').
Используя уравнение
непрерывности, он получил: 
.
Далее он воспользовался
своим третьим уравнением, т.е. он приписал:
.
Полагаем, что
функция 
и её производная непрерывны в каждой
точке пространства. В последнем
соотношении поменяем дифференцирование
в пространстве и дифференцирование по
времени:
(5)
Подставляя (5)
в (4'),
получим: 
(6).
Выражение (6)
является дифференциальной формой закона
полного тока для нестационарного
процесса. Слагаемое 
имеет смысл объемной плотности
электрического тока. Вектор объемной
плотности тока смещения:
(7).
Анализируя (6), Максвелл сформулировал одно из двух своих важнейших своих положений:
Первое положение Максвелла: Переменное во времени электрическое поле приводит к появлению в пространстве магнитного поля.
Запишем (6) в виде проекций:
(6')
Дифференциальной форме (6) соответствует интегральная форма:
(8).
2.7. Второе уравнение Максвелла.
В результате обобщения многочисленных экспериментальных исследований Фарадей получил закон электромагнитной индукции:
(1)
Знак « - » говорит о том, что возбуждаемая в контуре Э.Д.С. как бы препятствует изменению магнитного потока ( правило Ленца).
Из (1)следует, что величина Э.Д.С. не зависит от материала, из которого изготовлен контур. Очевидно, что ток, возбуждаемый в контуре зависит от сопротивления проводника.
Максвелл установил, что причиной возникновения э.д.с. в проводящем контуре является соленоидальное электрическое поле, которое возникает в пространстве и в отсутствие контура. Э.д.с. не зависит от свойств материала, но ток связан с его сопротивлением.
И
нтеграл
по замкнутому контуру (рисунок
правовинтовой системы) не равен нулю.
Рассмотрим в пространстве некий контур
l, поверхность S, на которую опирается
этот контур и единичную нормаль.
Положительное направление обхода
связано с направлением единичной нормали
правилом правого винта. Магнитный поток,
пересекающий контур, считается
положительным или отрицательным в
зависимости от того, совпадает он или
нет с направлением единичной нормали.
Скорость изменения магнитного потока
считается положительной или отрицательной
в зависимости от того, увеличивается
или уменьшается магнитный поток. Запишем
обобщения для электромагнитной индукции
через вектора электромагнитного поля:
.
Магнитный поток,
пересекающий поверхность S:
.
Подставляя эти соотношения в выражение(1),
получим:
(2).
Преобразуем левую часть, используя теорему Стокса:
Так как поверхность
S и контур L выбраны произвольно, то 
(3).
Выражение (3) является дифференциальной формой обобщенного закона электромагнитной индукции, а выражение (2) — его интегральной формой.
Второе положение Максвелла: Переменное магнитное поле возбуждает в пространстве соленоидальное электрическое поле.
