8.2. Потери энергии в проводниках.

На поверхности реальных проводников. Это является причиной потока энергии направленного внутрь проводящей среды. Получим соотношения для мощности потерь в проводящей среде.

Будем считать, что размеры проводящего тела и минимальный радиус кривизны >> d (глубина проникновения). Это условие применимости приближенных гр. усл. Щ-Л. В этом случае поток энергии направленный внутрь среды определяет Джоулевы потери. Предположим, что на поверхности S задана компонента Н_:

Е_ можно вычислить из гр. условия Щ-Л:

Используя выражения для Е и Н, определим плотность потока энергии, направленной внутрь проводящей среды:

,

.

Таким образом: .

Здесьимеет отрицательное значение т. к. поток направлен внутрь проводящей среды, а нормаль является внешней по отношению к среде.

Если размеры тела >> d (глубина проникновения) т. е. поток энергии проходит сквозь тело, то путем интегрирования вектора П по замкнутой поверхности S проводящего тела можно вычислить комплексную мощность потерь: .

Учитывая, что векторный элемент площади , получим:

, ,

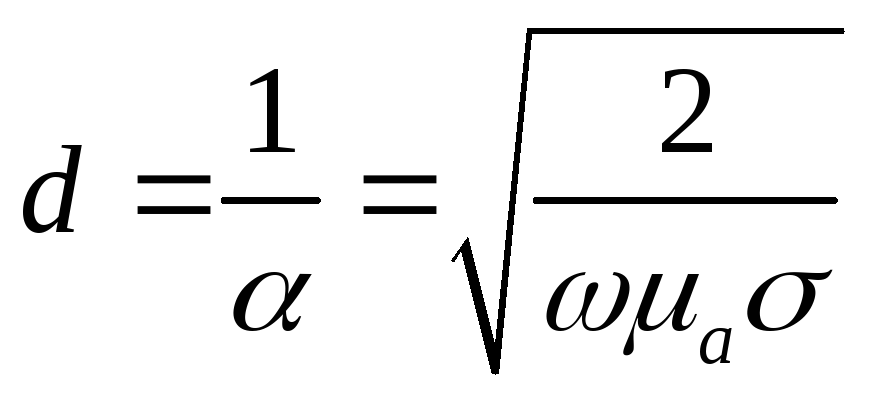Для того чтобы вычислить поток комплексной мощности необходимо осуществить интегрирование. Если размеры тела велики, то поток комплексной мощности будет совпадать с комплексной мощностью потерь.

Таким образом: (1)

Среднее за период значение комплексной мощности потерь:

(2)

8.3. Эквивалентный поверхностный ток.

В предыдущих параграфах было отмечено, что в проводящих средах на ВЧ электрический ток в проводниках сосредоточен в тонком приграничном слое. Для упрощения решения электродинамических задач вместо реального электрического тока протекающего в тонком, но конечном по величине, приграничном слое вводят эквивалентный поверхностный ток, т. е. ток, протекающий в бесконечно тонком приграничном слое.

Получим соотношения для его определения. Для этого будем предполагать, что проводящая среда занимает нижнее полупространство. В проводящей среде выделим брусок шириной l, боковые грани параллельны силовым линиям. Ширинуl выбираем таким образом, чтобы в пределах этого бруска амплитуды электрического тока и магнитного поля можно считать неизменными. Учитывая, что в проводящих средах амплитуда тока смещения пренебрежимо мала по сравнению с током проводимости, можно записать:

(1)

,

где под контуром интегрирования L подразумевают контур соответствующий поперечному сечению бруска. В соответствии с оговоренным условием о равенстве электрического тока и магнитного поля в пределах dl интегралы на участках контура перпендикулярного границе раздела будут равными по величине и противоположными по знаку. Кроме того, интегрирование по участку бесконечно удаленному от границы раздела даст нулевой результат т. к. поле будет равно 0.

В точке А выделим систему единичных векторов. Направление обхода L связано с направление правого винта.

Таким образом:

Будем полагать известной тангенциальную компоненту маг. поля на поверхности проводящей среды

Учитывая , а также неизменность маг. поля в пределах dl:

(2)

Мы получили, что .

Если предположить, что ток сосредоточен в бесконечно тонком слое, получим:

(3)

Используя систему единичных векторов:

(4)

Соотношения, определяющие эквивалентный поверхностный ток через тангенциальную компоненту маг. поля совпадают с известным гр. условием для Н составляющей на поверхности идеального проводника.