7.10. Приближенные граничные условия Щукина-Леантовича.
Самой распространенной задачей является задача присутствия реальных проводящих сред. Решение подобных задач существенно упрощается при использовании приближенных граничных условий Щукина-Леантовича (гр. усл. Щ-Л).
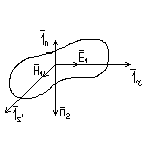
В отличие от традиционных граничных условий, которые устанавливают взаимосвязь между составляющими поля на границе раздела в разных средах, гр. усл. Щ-Л устанавливают взаимосвязь в одной среде. Из предыдущего параграфа известно, что если 2-ая среда является реальным проводником, то преломленная в ней волна распространяется перпендикулярно к границе раздела и составляющие поля преломленной волны можно описать теми же соотношениями, что плоскую волну в однородном изотропном пространстве.
(1),
где
—
нормаль к границе раздела направленная
в сторону проводящей среды.
Составляющие поля преломленной волны находятся в плоскости параллельной границе раздела.
На границе раздела S должны выполняться условия:
на
S (2)
Тогда, с учетом (2), (1) можно переписать:
(3)
В (3) вектор Н можно представить в полной форме:
,
потому, что
(4)
—
приближенное гр. усл. Щ-Л.
Устанавливает взаимосвязь между тангенциальными составляющими в 1-ой среде на границе раздела с хорошо проводящей средой.
Из
(4)
следует, что на поверхности реальных
проводников имеется малая по величине,
но конечная тангенциальная составляющая
компонента Е.
Е
и Н
на поверхности реальных проводников
определяют поток энергии направленной
внутрь проводящей среды: 
,
где zС2
— очень малая величина. При
и получаем:
—
гр. усл. на поверхности идеальных
проводников.
В основе наших рассуждений стоит предположение о том, что д=0 т. е. преломленная волна распространяется перпендикулярно к поверхности. В действительности она распространяется под очень малым углом к нормали. Приближенность состоит в том, что мы предполагаем этот угол равным 0.
Тангенциальная
компонента магнитного поля на поверхности
реальных металлов мало отличается от
тангенциальной компоненты на поверхности
идеального проводника. поэтому при
решении задач и используются гр. усл.
Щ-Л. Обычно предполагают: 
.
Раздел 8. Поверхностный эффект.
8.1. Явление поверхностного эффекта.
В
предыдущих параграфах было показано,
что переменное электромагнитное поле,
а стало быть и объемная плотность тока
проводимости, в проводящих средах
экспоненциально убывают при удалении
от границы раздела (
).
Т. е. на высоких частотах поле и ток
оказываются сосредоточенными в тонком
приграничном слое. Это явление получило
названиеповерхностного
или скин-эффекта
(пов. эф.).
В следствии пов. эф. эффективное поперечное сечение проводника оказывается существенно меньше его геометрического сечения, что является причиной увеличения активного сопротивления.
С другой стороны пов. эф. позволяет создавать защитные металлические экраны, предотвращающие воздействие электромагнитного поля на радиотехнические устройства.
Следует подчеркнуть, что в случае постоянного или низкочастотного электромагнитного поля металлические экраны выполняются из диа- и парамагнитных материалов. Это позволяет осуществить защиту от электрического поля, но не экранизирует магнитное поле.
Если толщина металлического экрана превышает несколько “ d ” (глубина проникновения) и экран является замкнутым окружая изолированную область, то можно считать что внутри электромагнитное поле отсутствует.