
- •7.7.Условия возникновения полного внутреннего отражения.
- •7.8. Диэлектрик и идеальный проводник.
- •Характеристическое сопротивление идеальной проводящей среды равно нулю при: .
- •7.9. Падение плоской волны на границу поглощающей среды.
- •7.10. Приближенные граничные условия Щукина-Леантовича.
- •Раздел 8. Поверхностный эффект.
- •8.1. Явление поверхностного эффекта.
- •8.2. Потери энергии в проводниках.
- •8.3. Эквивалентный поверхностный ток.
- •8.4 Поверхностные сопротивления.
- •Раздел 9. Элементарные излучатели.
- •9.1. Элементарный электрический излучатель.
Найдем модуль:

так
как при
![]() :
: 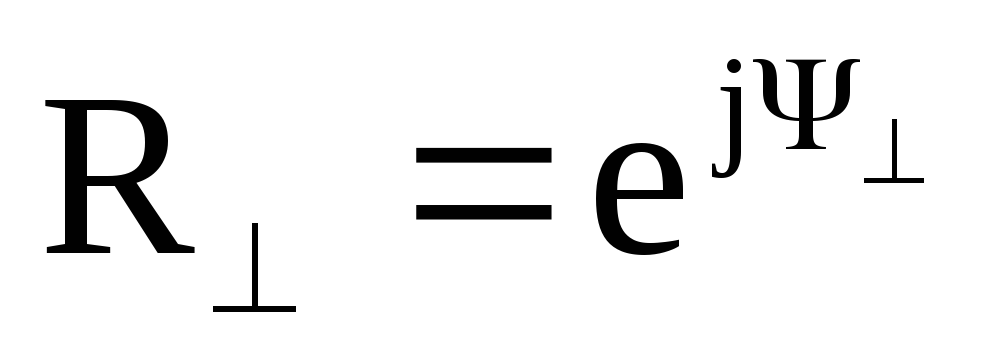 (7)
(7)
![]() (8)
(8)
Из (7) и (8) следует, что плотность потока энергии одинакова в падающей и отраженной волнах.
7.7.Условия возникновения полного внутреннего отражения.
1
условие:
![]() так как sin<1
то k2<k1
так как sin<1
то k2<k1
Вторая среда должна быть оптически менее плотная, чем первая
2
условие:
![]() Получим выражение для структуры поля,
результирующей волны в первой среде
при
Получим выражение для структуры поля,
результирующей волны в первой среде
при![]()
![]()
![]() ,
, ![]()
 ,
,
![]()
![]()
 ,
,
![]()
![]() ,
,
![]()
В
нашем случае коэффициенты: 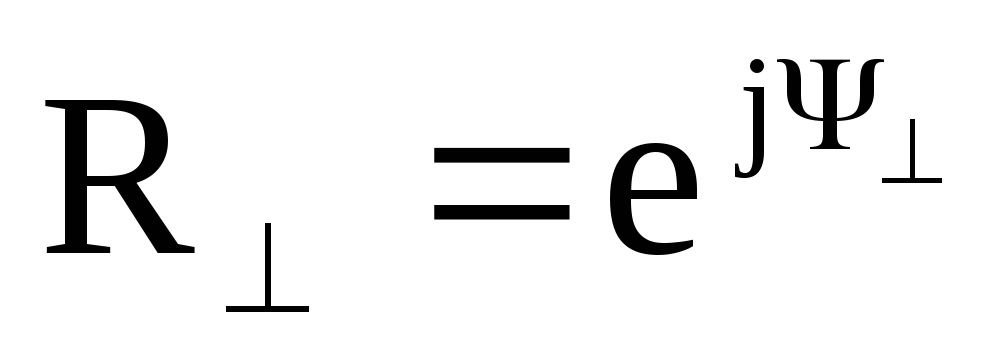 ,
,![]()
Для
свертки соотношений надо вынести за
круглую скобку множитель
![]() .
.
С учетом проделанных преобразований:
![]()
![]()
![]() ,
,
![]()
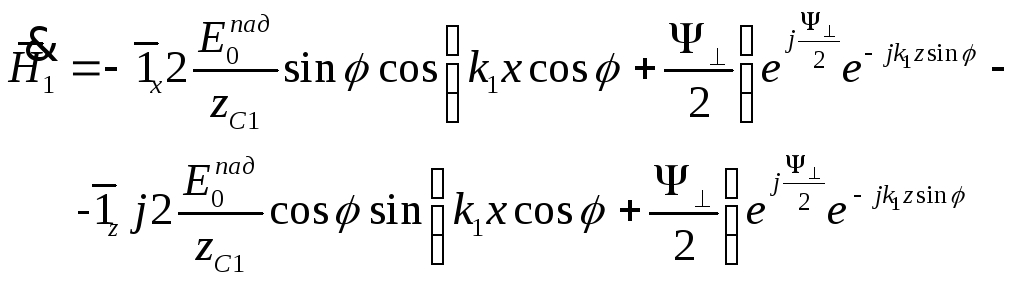 ,
,
![]()
![]()
![]()
 ,
,
![]()
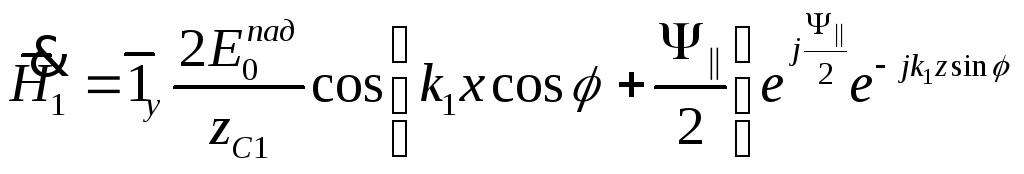 ,
,
![]()
Из полученных соотношений следует:
1. Поле в первой среде является плоской волной.
2. Поверхности равных фаз образуют семейство плоскостей,
перпендикулярных оси Z, т.е. определяется уравнением Z=const.
3. Амплитуда плоских волн зависит от угла падения и координаты Х.
4. Поверхность равных амплитуд определяется уравнением X=const.
5. Поверхность равных амплитуд не совпадает с поверхностью равных фаз.
6. Плоские волны являются неоднородными.
7. Плоские волны в первой среде распространяются вдоль оси Z, т.е. вдоль границы раздела, такие волны называются направляемыми.
И в случае перпендикулярной и параллельной поляризации плоские волны имеют составляющую поля в направлении распространения (в случае перпендикулярной поляризации Нz, в случае параллельной поляризации Ez), т.е. полученные решения представляют собой плоскую, неоднородную, не поперечную волну.
Определим фазовую скорость.
Общее
выражение: ![]()
В
нашем случае: ![]()
Проанализируем: ![]()
при
![]()
![]() ;
;![]()
![]() ,
, ![]()
![]() (9)
(9)
Из
выражения (9)
видно, что направляющая волна
распространяется с фазовой скоростью,
которая превышает фазовую скорость
плоской волны в свободном пространстве
с параметрами первой среды, но меньше
фазовой скорости в свободном пространстве
с параметрами второй среды. Определяем
длину волны в направлении распространения:
![]()
Или в данном случае:
![]() (10)
(10)
![]() (11)
(11)
Из
соотношений при
![]() следует, что в направлении, перпендикулярном
границе раздела (параллельной оси Х),
поле имеет характер стоячей волны с
пространственным периодом или длинной
волны.
следует, что в направлении, перпендикулярном
границе раздела (параллельной оси Х),
поле имеет характер стоячей волны с
пространственным периодом или длинной
волны.

![]()
Глядя
на эти же соотношения, можно отметить,
что поперечные, относительно направления
распространения поля, компоненты поля
(![]() )—синфазны.
Продольная, относительно поперечных,
имеет фазовый сдвиг 90 (Z).
)—синфазны.
Продольная, относительно поперечных,
имеет фазовый сдвиг 90 (Z).
Определим энергетические параметры. Определим комплексный вектор Пойнтинга:
 (12)
(12)
В выражении (12) знак "+" соответствует нормальной поляризации, а знак "-" для параллельной поляризации. Как следует из (12) комплексный вектор Пойнтинга имеет реальную и мнимую части.
![]()
Среднее за период значение вектора Пойнтинга направлено вдоль оси Z.
![]() (13)
(13)
Т.е. в среднем за период энергия переносится вдоль оси Z. В направлении, перпендикулярном границе раздела существует реактивный поток мощности. Из (*) видно, что имеется бесконечное количество плоскостей, перпендикулярных оси Х (параллельных границе раздела), в которых Е и Нn обращаются в нуль. Точки пересечения этих плоскостей с осью Х можно определить из следующего соотношения:
![]()
В случае параллельной поляризации, параллельной границе раздела, будет параллельна и компонента Еz. Из предыдущего соотношения следует:
![]()
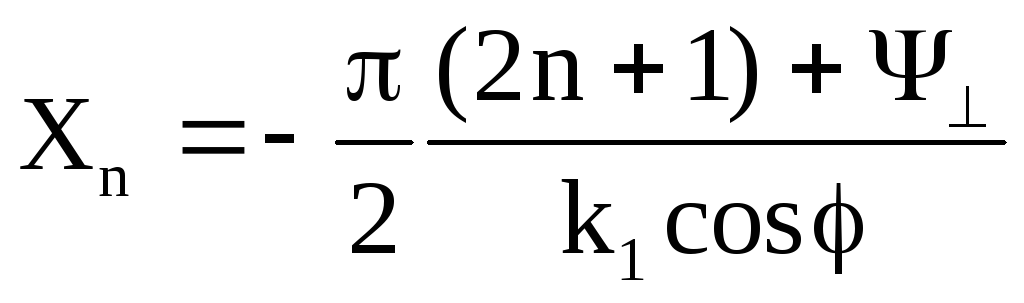 (14)
(14)
где n=1, 2, 3, ...
Из приведенных рассуждений следует, что в плоскостях, параллельных границе раздела, положение которых описывается в (14), автоматически удовлетворяет граничные условия, соответствующие граничным условиям на поверхности идеального проводника (Е=0, Нn=0).
Если
мы одну из этих плоскостей заменим
идеально проводящей поверхностью (Хn),
то получим, что при
![]() (т.е. над плоскостью в первой среде) поле
останется неизменным.
(т.е. над плоскостью в первой среде) поле
останется неизменным.
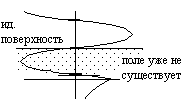
Еще характерная особенность этих плоскостей (14) заключается в том, что поток энергии через эти поверхности (как активной, так и реактивной) равна нулю.
Определим среднее за период значение скорости распространения энергии в первой среде.
В
первой среде при
![]() выделим
энергетическую трубку, т. е. часть
пространства, через боковые поверхности
которого отсутствует перенос энергии,
т. е.
выделим
энергетическую трубку, т. е. часть
пространства, через боковые поверхности
которого отсутствует перенос энергии,
т. е.![]() .
.
В качестве энергетической трубки удобно взять часть пространства, ограниченное соседними поверхностями, положение которых определяется (14). Например, Xn , Xn+1.
В этом случае, учитывая, что составляющая поля зависит от координаты Х, выражение для скорости распространения энергии включает обязательно интегрирование. Подставляя соответствующие компоненты и осуществляя интегрирование, получим:
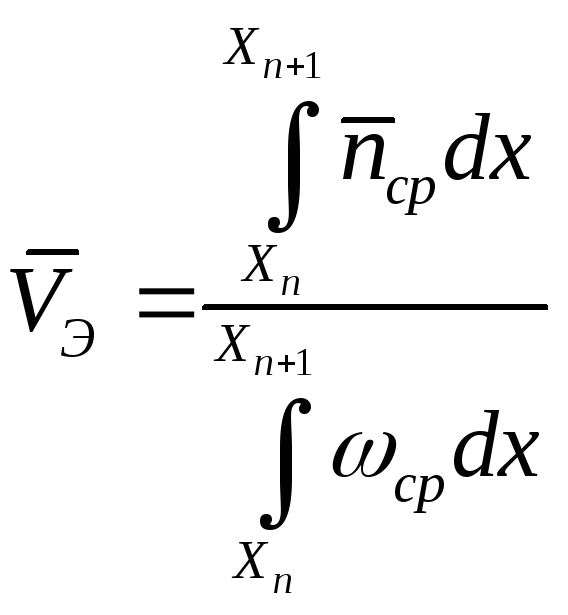 (15)
(15)
![]() (16)
(16)
![]()
И з(16)
видно, что скорость распространения
энергии в первой среде меньше скорости
света в первой среде.
з(16)
видно, что скорость распространения
энергии в первой среде меньше скорости
света в первой среде.
Выражение
для фазовой скорости:
![]()
![]()
Рассмотрим результирующее поле во второй среде при выполнении условия ПВО.
Исходные соотношения:
![]()
![]() ,
,
![]() (1)
(1)
![]() ,
,
![]() (2)
(2)
![]()
![]()
![]() ,
,
![]() (3)
(3)
![]() ,
,
![]() (4)
(4)
При
![]() :
:![]() является
чисто мнимой величиной.
является
чисто мнимой величиной.
Удобно
ввести обозначение: ![]() (5)
(5)
где
при
![]() является действительной величиной
является действительной величиной![]() (6)
(6)
И з
закона Снелиуса:
з
закона Снелиуса:![]()
![]()


![]()
Минус в (5) выбран из физических соображений.
Подставляя
(5)
в (1)—(4)
и учитывая, что
![]() получим:
получим:
![]()
![]() ,
,
![]() (7)
(7)
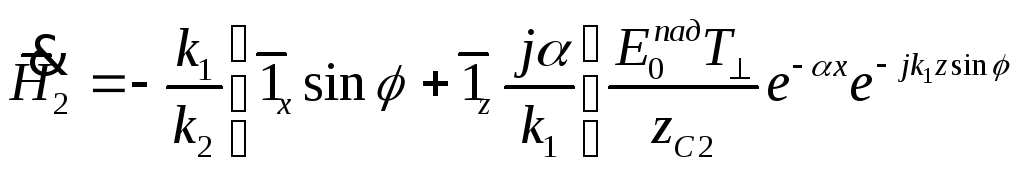 ,
,
![]() (8)
(8)
![]()
 ,
,
![]() (9)
(9)
![]() ,
,
![]() (10)
(10)
Из
(7) - (10)
видно, что при
![]() поле во второй среде имеет характер
плоской волны (поверхность равных фаз
определяется уравнением Z=const)
распространяется вдоль границы раздела.
Поверхность равных амплитуд (X=const)
перпендикулярна поверхности равных
фаз (Z=const), т.е. плоская волна является
плоской неоднородной. В направлении
распространения вдоль оси Z имеются
составляющие поля (Нz
при перпендикулярной поляризации и Еz
при параллельной поляризации), т. е.
плоская неоднородная волна является
не поперечной. Фазовая скорость волны
и длина волны определяется теми же
соотношениями, что и для волны в первой
среде:
поле во второй среде имеет характер
плоской волны (поверхность равных фаз
определяется уравнением Z=const)
распространяется вдоль границы раздела.
Поверхность равных амплитуд (X=const)
перпендикулярна поверхности равных
фаз (Z=const), т.е. плоская волна является
плоской неоднородной. В направлении
распространения вдоль оси Z имеются
составляющие поля (Нz
при перпендикулярной поляризации и Еz
при параллельной поляризации), т. е.
плоская неоднородная волна является
не поперечной. Фазовая скорость волны
и длина волны определяется теми же
соотношениями, что и для волны в первой
среде:
![]() ,
, ![]() ,
,![]()
![]() ,
, ![]()
Характерное отличие: амплитуда плоской волны экспоненциально убывает от границы раздела, т. е. поле существует в некотором приграничном слое. Направляемые волны, амплитуды которых экспоненциально затухают при удалении от границы раздела, называются поверхностными.
Проанализируем, в каких пределах изменяется — коэффициент, характеризующий уменьшение амплитуды волны в направлении перпендикулярном границе раздела.
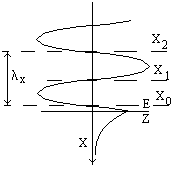
![]()
является действительным коэффициентом.
При изменении
является действительным коэффициентом.
При изменении
![]()
изменяется
так:
![]() .
.
Для
вычисления скорости распространения
энергии в качестве энергетической
трубки следует взять часть пространства,
которое простирается от
![]() до
до![]() .
Вектор
Пойнтинга
в 1-ой среде:
.
Вектор
Пойнтинга
в 1-ой среде:
![]()
Положение
координаты Х0
определяется из:
![]()
![]() ,
, 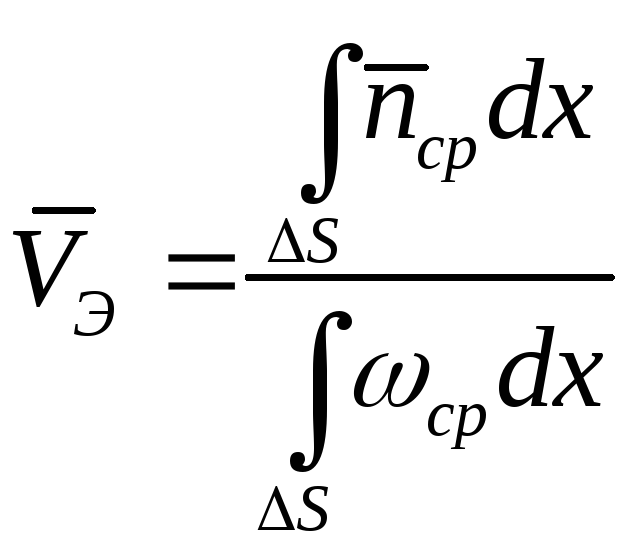
В данном случае интегрирование осуществляется не по площади, а по координате Х.
 ,
,
![]()
Скорость распространения энергии во 2-ой среде определяется тем же соотношением, что и в 1-ой среде.
