
Математическая экономика
.pdf5. Задача об оптимальном распределении заданного потока в транспортной сети
Величину потока P0 , подлежащую распределению по сети, принять равной Pmax −∆P , ∆P – величина, задаваемая преподавателем для каждой учебной группы.
Ниже приведены матрицы удельных стоимостей, которые следует взять для расчетов по соответствующему варианту.
|
№ 5-1 |
|
|
|
|
№ 5-2 |
|
|
|
|
№ 5-3 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
50 |
20 |
|
|
|
x1 |
|
12 |
11 |
7 |
|
|
x1 |
|
1 |
7 |
10 |
|
|
x2 |
|
|
8 |
5 |
|
x2 |
|
|
|
10 |
7 |
|
x2 |
|
|
|
10 |
19 |
|
x3 |
|
|
|
|
10 |
x3 |
|
|
|
|
|
2 |
x3 |
|
|
|
|
|
4 |
x4 |
|
20 |
|
|
5 |
x4 |
|
|
9 |
|
13 |
|
x4 |
|
|
14 |
|
16 |
|
x5 |
|
|
10 |
|
3 |
x5 |
|
|
|
|
|
5 |
x5 |
|
|
8 |
|
|
14 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
№ 5-4 |
|
|
|
|
№ 5-5 |
|
|
|
|
№ 5-6 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
9 |
3 |
4 |
|
|
x1 |
|
4 |
7 |
|
|
|
x1 |
|
2 |
9 |
|
|
|
x2 |
|
|
11 |
17 |
|
x2 |
|
|
|
|
5 |
|
x2 |
|
|
|
15 |
27 |
|
x3 |
|
|
|
|
2 |
x3 |
|
|
|
18 |
|
12 |
x3 |
|
|
|
|
|
11 |
x4 |
|
15 |
|
14 |
|
x4 |
|
7 |
|
|
8 |
12 |
x4 |
|
|
25 |
|
|
6 |
x5 |
|
21 |
|
|
16 |
x5 |
|
|
|
|
|
14 |
x5 |
|
|
|
12 |
|
16 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
№ 5-7 |
|
|
|
|
№ 5-8 |
|
|
|
|
№ 5-9 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
5 |
12 |
19 |
|
|
x1 |
|
7 |
17 |
10 |
11 |
|
x1 |
|
45 |
3 |
4 |
|
|
x2 |
|
|
11 |
10 |
|
x2 |
|
|
|
|
8 |
19 |
x2 |
|
|
|
11 |
15 |
|
x3 |
|
|
|
|
15 |
x3 |
|
|
|
16 |
|
11 |
x3 |
|
|
|
|
|
5 |
x4 |
|
|
5 |
10 |
|
x4 |
|
|
|
|
17 |
|
x4 |
|
|
13 |
|
25 |
|
x5 |
|
|
|
|
6 |
x5 |
|
|
|
|
|
2 |
x5 |
|
|
15 |
|
|
6 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
131
|
№ 5-10 |
|
|
|
|
№ 5-11 |
|
|
|
|
№ 5-12 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
5 |
24 |
|
|
|
x1 |
|
5 |
17 |
|
|
|
x1 |
|
5 |
11 |
|
|
|
x2 |
|
|
17 |
3 |
|
x2 |
|
|
|
|
42 |
|
x2 |
|
|
|
|
45 |
|
x3 |
|
|
|
|
12 |
x3 |
|
|
|
18 |
|
2 |
x3 |
|
|
|
25 |
|
18 |
x4 |
|
1 |
|
|
7 |
x4 |
|
10 |
|
|
5 |
14 |
x4 |
|
8 |
|
|
7 |
10 |
x5 |
|
|
11 |
|
14 |
x5 |
|
|
|
|
|
11 |
x5 |
|
|
|
|
|
8 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
№ 5-13 |
|
|
|
|
№ 5-14 |
|
|
|
|
№ 5-15 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
17 |
5 |
18 |
20 |
|
x1 |
|
50 |
1 |
|
|
|
x1 |
|
3 |
9 |
17 |
|
|
x2 |
|
|
|
9 |
3 |
x2 |
|
|
|
5 |
18 |
|
x2 |
|
|
|
6 |
11 |
|
x3 |
|
|
20 |
|
14 |
x3 |
|
|
|
|
|
14 |
x3 |
|
|
|
|
|
20 |
x4 |
|
|
|
31 |
|
x4 |
|
|
15 |
|
|
10 |
x4 |
|
|
15 |
|
23 |
|
x5 |
|
|
|
|
8 |
x5 |
|
|
|
20 |
|
7 |
x5 |
|
|
|
|
|
5 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
№ 5-16 |
|
|
|
|
№ 5-17 |
|
|
|
|
№ 5-18 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
5 |
30 |
3 |
15 |
|
x1 |
|
8 |
7 |
|
|
|
x1 |
|
7 |
10 |
5 |
|
|
x2 |
|
|
|
10 |
19 |
x2 |
|
|
|
16 |
31 |
|
x2 |
|
|
|
6 |
8 |
|
x3 |
|
|
5 |
|
11 |
x3 |
|
|
|
|
|
13 |
x3 |
|
|
|
|
|
15 |
x4 |
|
|
|
15 |
|
x4 |
|
|
19 |
|
|
7 |
x4 |
|
|
7 |
|
15 |
|
x5 |
|
|
|
|
16 |
x5 |
|
|
|
11 |
|
5 |
x5 |
|
|
|
|
|
2 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
№ 5-19 |
|
|
|
|
№ 5-20 |
|
|
|
|
№ 5-21 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
35 |
6 |
|
|
|
x1 |
|
1 |
32 |
5 |
14 |
|
x1 |
|
5 |
30 |
20 |
|
|
x2 |
|
|
|
1 |
|
x2 |
|
|
|
|
14 |
20 |
x2 |
|
|
|
15 |
15 |
|
x3 |
|
|
26 |
|
16 |
x3 |
|
|
|
15 |
|
10 |
x3 |
|
|
|
|
|
10 |
x4 |
13 |
|
|
17 |
11 |
x4 |
|
|
|
|
17 |
|
x4 |
|
|
10 |
|
20 |
|
x5 |
|
|
|
|
4 |
x5 |
|
|
|
|
|
10 |
x5 |
|
|
10 |
|
|
20 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
132
|
№ 5-22 |
|
|
|
|
№ 5-23 |
|
|
|
|
№ 5-24 |
|
|
||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
2 |
40 |
|
|
|
x1 |
|
45 |
2 |
|
|
|
x1 |
|
4 |
7 |
|
|
|
x2 |
|
|
|
11 |
|
x2 |
|
|
|
10 |
3 |
|
x2 |
|
|
|
|
35 |
|
x3 |
|
|
32 |
|
19 |
x3 |
|
|
|
|
|
15 |
x3 |
|
|
|
27 |
|
12 |
x4 |
13 |
|
|
2 |
12 |
x4 |
|
|
7 |
|
|
10 |
x4 |
|
12 |
|
|
10 |
11 |
x5 |
|
|
|
|
19 |
x5 |
|
|
|
10 |
|
20 |
x5 |
|
|
|
|
|
10 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
№ 5-25 |
|
|
|
|
№ 5-26 |
|
|
||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x1 |
5 |
21 |
|
|
|
x1 |
|
20 |
17 |
|
|
|
x2 |
|
|
16 |
4 |
|
x2 |
|
|
|
|
14 |
|
x3 |
|
|
|
|
14 |
x3 |
|
|
|
6 |
|
19 |
x4 |
|
8 |
|
|
9 |
x4 |
|
5 |
|
|
10 |
7 |
x5 |
|
|
10 |
|
14 |
x5 |
|
|
|
|
|
16 |
x6 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
133
Глава 5. НЕЛИНЕЙНЫЕ ЗАДАЧИ СТАТИЧЕСКОЙ ОПТИМИЗАЦИИ
§ 5.1. Аналитическое решение нелинейных задач статической оптимизации
Рассмотрим задачу оптимизации об отыскании значений x |
= x0 |
i |
i |
(i =1,n ), образующих вектор x = x 0 , при которых ЦФ y = f (x) принимает наименьшее (либо наибольшее) значение при выполнении условий-
ограничений: h j (x) = 0, gl (x) ≥ 0; j =1,m, l =1,k.
Как отмечалось в гл. 1, в частных случаях задача оптимизации может не содержать ограничений. При этом решение задачи, если оно существует, совпадает с одним из локальных экстремумов ЦФ, называемым глобальным экстремумом. Отыскание решения задачи безусловной оптимизации сводится к выявлению всех локальных экстремумов, вычислению в каждом из них ЦФ и выбору наименьшего из минимумов (либо наибольшего из максимумов).
При нахождении локальных экстремумов используется необходимое условие экстремума, в соответствии с которым в экстремальной точке
x = x 0 все частные производные дифференцируемой функции равны нулю:
∂y |
|
|
|
|
|
∂f |
|
∂f |
T |
|
|
|
|
|
|
||||||
|
= 0, |
i =1,n |
или f = gradf = 0, f = |
|
,..., |
|
|
. (5.1) |
||
∂x |
∂x |
∂x |
||||||||
i |
|
|
|
|
|
1 |
|
n |
|
|
Точки, удовлетворяющие (5.1), называются стационарными. Следует подчеркнуть, что все экстремумы дифференцируемой функции находятся среди стационарных точек, но среди стационарных точек могут оказаться и не экстремальные. Заметим, что экстремум может оказаться в точке, где функция не дифференцируема.
Для того чтобы проверить, является ли стационарная точка x 0 экс-
тремальной и определить ее характер (min или max), можно использовать достаточное условие экстремума. Оно формулируется с помощью матрицы
H вторых производных, обозначаемой 2 f и называемой матрицей Гессе.
∂2 f
Ее элементы hij = ∂xi∂x j .
Если f (x) имеет в некоторой окрестности стационарной точки непрерывные вторые частные производные, то в случае, когда матрица Гессе
134

отрицательно определена, точка x 0 является точкой максимума, а в случае,
когда она положительно определена, x 0 – точка минимума.
Матрица Н положительно определена, когда все ее определители ∆i (i =1,n) , получаемые выделением первых i строк и i столбцов, поло-
жительны; если же (−1)i ∆i > 0 для i =1,n , то матрица отрицательно оп-
ределена.
Рассмотренные условия позволяют в некоторых случаях получить решение поставленной оптимизационной задачи.
Пример 1. Исследовать на экстремум функцию
y = 30 + x13 + 3x1 x2 2 −15x1 −12x2.
Решение. Используя условие (5.1), получаем:
∂y |
= 3x2 |
+ 3x2 |
−15 = 0; |
x2 |
+ x2 |
= 5; |
|||
|
|||||||||
1 |
|
2 |
|
1 |
|
2 |
|
||
∂x1 |
|
|
|
|
|
|
|
||
|
∂y |
= 6x x |
2 |
−12 = 0; x x |
2 |
= 2. |
|
||
|
|
|
|||||||
|
∂x2 |
1 |
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
||
Подставив x2 = 2 / x1 в 1-е уравнение, полученную систему сводим к уравнению: x14 −5x22 + 4 = 0 . Решив его, получаем стационарные точки:
xA(1; 2), xB (2; 1), xC (−1; −2), xД(−2; −1).
Составляем матрицу Гессе
|
6x1 |
6x2 |
|
|
Н = 6x |
2 |
6x |
. |
|
|
|
1 |
|
|
Подставляя в Н координаты найденных точек, получаем:
6 12 |
|
|
∆ = 6 > 0 |
|
12 6 |
∆ =12 > 0 |
|
|
|
|||||
H A = |
, |
|
|
1 |
; |
HB = |
|
, |
1 |
|
|
|
; |
|
∆2 = −108 < 0 |
|
∆2 =108 > 0 |
|
|||||||||||
12 |
6 |
|
6 |
|
12 |
|
|
|||||||
−6 −12 |
, |
∆1 = −6 < 0 |
; HД = |
−12 −6 |
, |
∆1 = −12 < 0 |
. |
|||||||
HC = |
−6 |
|
∆2 = −108 |
< 0 |
|
−6 |
|
∆2 = |
108 > 0 |
|||||
−12 |
|
|
|
|
−12 |
|
|
|||||||
Анализируя знаки определителей, заключаем, что xB – точка мини-
мума, в ней ymin = 2 ; xД – точка максимума, в ней ymax =58; в x A и xC – экстремума нет.
Пример 2. В эксперименте регистрируется процесс yэ(t) , представляющий собой сумму плавно изменяющейся так называемой полезной со-
135
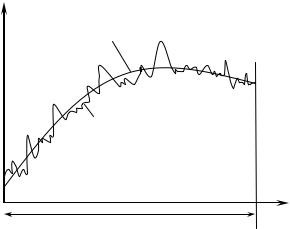
ставляющей и быстро изменяющейся компоненты, порожденной действием случайных факторов (рис. 5.1).
Требуется по результатам
y |
|
|
|
|
|
|
|
наблюдений |
yэ(t) , |
выполнен- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
а |
(t) |
|
|
|
|
|
|||||||||
|
|
|
y |
|
|
|
|
|
ным на промежутке [0, T], най- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
ти |
аналитическое |
описание |
|||||
|
|
|
|
|
|
|
|
|
|
|
процесса |
в |
виде |
|
некоторой |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
уэ(t) |
|
|
|
|
«плавной» |
|
функции |
yа (t) , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
сглаживающей |
получаемый |
||||||
|
|
|
|
|
|
|
|
|
t |
|
экспериментально |
|
процесс и |
|||||
0 |
|
|
|
Т |
|
|
|
приближенно воспроизводящей |
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
полезную |
составляющую |
про- |
|||||
|
|
|
|
Рис. 5.1 |
|
|
|
|
цесса. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Решение. Примем в каче- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
стве сглаживающей функции |
|||||||
|
|
|
|
yа(t) = А + А |
t |
+ A |
t |
2 , 0 ≤ t ≤T . |
|
|
(5.2) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 1 |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
T |
|
T |
|
|
|
|
|
|
|||
Ее параметры А0 , А1, А2 подберем так, чтобы интегральное квадратическое отклонение
|
2 |
|
|
|
|
t |
|
|
t |
2 |
2 |
||
T |
[yэ(t) − yа(t)] |
T |
|
|
|
||||||||
Q = ∫ |
dt = ∫ |
yэ(t) − A0 |
− A1 |
|
|
|
− A2 |
|
|
|
dt |
||
|
|
||||||||||||
0 |
|
|
|
|
T |
|
T |
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
||
было минимальным.
Используя необходимое условие экстремума (5.1), получаем:
|
|
|
∂Q |
|
T |
|
|
|
|
|
|
|
|
|
t |
|
|
|
t |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
∫ |
|
yэ(t) − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
= |
2 |
A0 − A1 |
|
|
− A2 |
|
|
|
|
(−1)dt = 0 , |
|
|
||||||||||||||||||||
|
|
|
∂A |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
T |
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
||||||||
или |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫yэ(t)dt. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
TA0 + |
|
|
A1 + |
|
|
A2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично рассматривая условие |
|
∂Q |
|
|
= 0 |
и |
|
∂Q |
|
= 0 |
, получаем сис- |
||||||||||||||||||||||||||
|
∂A |
|
|
|
∂A |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A + |
1 |
A + |
1 A |
= s |
; |
1 |
A + 1 A + 1 |
A |
= s |
; |
|
1 A + |
1 |
A + |
1 |
A |
= s |
, (5.3) |
|||||||||||||||||||
0 |
2 |
1 |
|
3 |
2 |
|
|
0 |
|
2 |
0 |
3 |
1 |
4 |
2 |
1 |
|
3 |
|
|
0 |
|
|
4 |
1 |
5 |
2 |
2 |
|
||||||||
136
|
|
|
|
1 T |
|
|
|
1 T |
|
t |
|
|
|
1 T |
|
t |
2 |
|
|||||
где s |
0 |
= |
|
|
∫ |
yэ(t)dt; s |
= |
|
|
∫ |
yэ(t) |
|
dt; s |
2 |
= |
|
|
∫ |
yэ(t) |
|
|
dt. |
(5.4) |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
T |
1 |
T |
T |
|
T |
T |
|
|
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Решив систему линейных алгебраических уравнений (5.3), получаем следующие выражения для неизвестных параметров аппроксимирующей параболы (5.2):
A |
|
=9s − |
36s +30s , |
|
|
|
0 |
|
0 |
1 |
2 |
|
(5.5) |
A1 |
= −36s0 |
+192s1 −180s2, |
||||
|
|
=30s0 −180s1 +180s2. |
|
|
||
A2 |
|
|
|
|||
Отметим, что в случае, когда процесс |
yэ(t) |
регистрируется в дис- |
||||
кретные моменты времени |
t0 = 0, t1 = h, t2 = 2h,..., tk = kh,..., |
tN = Nh = |
||||
=T , разбивающие промежуток [0, T ] на достаточно мелкие отрезки длины h, для вычисления интегралов (5.4), входящих в (5.5), можно использовать численные методы, в частности формулу прямоугольников [17]. Тогда
|
|
1 |
N |
э |
|
|
1 |
N |
э kh |
|
1 |
N |
э kh 2 |
||||
s0 |
≈ |
|
∑ y |
k |
; |
s1 ≈ |
|
∑ y |
|
; |
s2 ≈ |
|
∑ y |
|
|
, |
|
N |
N |
N |
|||||||||||||||
|
|
k =1 |
|
|
k =1 |
k |
T |
|
k =1 |
k |
T |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где ykэ = yэ(kh) .
Рассмотрим теперь задачу оптимизации, в которой наряду с ЦФ задана система ограничений-равенств, т.е. задачу на условный экстремум. Ее можно свести к задаче на безусловный экстремум, используя один из следующих двух приемов.
1. Допустим, что систему m уравнений удается разрешить относительно каких-либо m переменных из общего списка n неизвестных xi (m < n) , например:
x |
= ϕ (x |
,..., x ), |
|
||||
1 |
1 |
m+1 |
|
n |
|
|
|
x2 |
= ϕ2(xm+1,..., xn ), |
(5.6) |
|||||
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
x |
= ϕ |
m |
(x |
|
,..., x |
). |
|
m |
|
m+1 |
n |
|
|
||
Подставляя соотношения (5.6) в ЦФ, получаем задачу об отыскании n − m переменных xm+1,..., xn , при которых функция
y = f (ϕ (x |
,..., x ),...,ϕ |
m |
(x |
,..., x )) = f (x |
,..., x ) |
(5.7) |
||
1 |
m+1 |
n |
m+1 |
n |
m+1 |
n |
|
|
принимает наименьшее значение. Подставив полученные в результате решения задачи на безусловный экстремум для функции (5.7) значения
xm0 +1,...., xn0 в (5.6), находим полный набор неизвестных x10 ,...., xn0 . 2. Для задачи (1.7) – (1.8) введем вспомогательную функцию:
137

m
y = f (x) + ∑ λk hk (x) ,
k =1
называемую функцией Лагранжа. В нее входят: заданная ЦФ f, выражения hk , стоящие в левых частях ограничений-равенств (1.8), и вспомогательные переменные λk , называемые множителями Лагранжа.
Для решения задачи в этом случае можно использовать необходимое |
||||||||||
~ |
|
|
|
~ |
|
|
|
|
||
условие |
∂y |
= 0, i = |
|
; |
|
∂y |
= 0, j = |
|
|
|
1, n |
1, m. |
|
||||||||
|
|
|
||||||||
|
∂xi |
|
∂λj |
|
||||||
Пример. Для формализованной в примере 1 из § 1.1 задачи найдем |
||||||||||
параметры R и Н, при которых ЦФ: |
|
|||||||||
|
|
|
|
|
s = 2πR2 + 2πRH |
(5.8) |
||||
минимальна при выполнении условия |
|
|||||||||
|
|
|
|
|
πR2H −V = 0. |
(5.9) |
||||
|
|
|
|
|
0 |
|
|
|
||
Используя метод исключения, из (5.9) выражаем H =V0 / πR2 .
Подставляя это соотношение в (5.8), получаем ЦФ: s = 2πR2 + 2VR0 ,
зависящую только от R. Из условия |
|
ds / dR = 4πR − 2V / R2 |
= 0 находим |
||||||||||
|
|
|
|
V0 |
|
|
V0 |
|
|
|
|
0 |
|
R* = 3 V / 2π; H* = |
|
( |
)−2 / 3 = 2 |
3 V / 2π = 2R*. |
|||||||||
|
|
|
|||||||||||
|
|
0 |
|
π |
|
|
2π |
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
||||
Заметим, что при найденных значениях параметров R= R* и Н=Н*: |
|||||||||||||
|
d 2s |
= 4π+ 2V |
1 |
= |
4π+ 4V |
|
1 |
|
=12π > |
0, |
|||
|
dR2 |
|
|
/ 2π |
|||||||||
|
0 R3 |
|
|
|
|
0 V0 |
|
|
|||||
следовательно, эти параметры действительно дают минимум s.
Пользуясь методом множителей Лагранжа, сформируем функцию: s = 2πR2 + 2πRH + λ(πR2H −V0 ) и для нее запишем условия:
|
∂s |
= 4πR + 2πH + 2πλRH |
= 0; |
||||||
|
|
||||||||
∂R |
|||||||||
|
|
∂s |
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
= 2πR |
+ πλR2 = 0; |
|
||||
|
|
|
|
|
|
|
|||
|
|
∂H |
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
∂s |
= πR2H −V = 0. |
|
|||
|
|
|
|
|
|
||||
|
|
|
∂λ |
|
0 |
|
|||
|
|
|
|
|
|
|
|||
Из второго уравнения получаем λ* = −2/ R . Подстановка этого соот- |
|||||||||
ношения в 1-е уравнение дает 4πR + 2πH − 4πH = 0; |
H* = 2R* . |
||||||||
138
Задача, в которой ЦФ (1.7) рассматривается при наличии ограниче- ний-неравенств (1.9), относится к задачам математического (нелинейного) программирования. При этом обычно неравенства (1.9) задают в пространстве переменных x1,..., xn некоторую замкнутую ограниченную область D.
Следовательно, нужно найти такую точку x D , для которой ЦФ (1.7) является наименьшей (или наибольшей). Ясно, что искомая точка может оказаться внутри D, тогда она является точкой экстремума, либо на границе D. Учитывая это, для решения рассматриваемой задачи можно поступить следующим образом:
1)найти все локальные экстремумы ЦФ (1.7), выбрать те из них, которые удовлетворяют (1.9), т.е. лежат в D, а остальные исключить из рассмотрения;
2)вычислить ЦФ в выделенных точках;
3)найти наибольшие (или наименьшие) значения ЦФ на линиях (поверхностях), образующих границу D;
4)из всех найденных значений (в п. 2 и 3) выбрать наибольшее (наименьшее).
Пример. Найти наибольшее и наименьшее значения ЦФ:
|
|
|
|
|
|
y = x2 |
+ x |
2 |
− x x |
2 |
+ x + x |
2 |
|
|
|||||
при выполнении условий: |
|
1 |
|
|
2 |
1 |
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x1 ≤ 0, x2 ≤ 0, x1 + x2 ≥ −3. |
|
|
||||||||||||
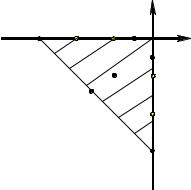
Эти условия задают область D в виде тре- |
|
|
x |
||||||||||||||||
угольника ОАВ (рис. 5.2). |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
-3А -2 -1 P4 |
0 x1 |
||||||||
Решение 1. Находим стационарные точки |
|||||||||||||||||||
из условий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 |
D |
P3 |
||
|
|
|
∂y / ∂x1 = 2x1 − x2 +1 = 0; |
|
|
|
|
|
|
P0 |
-1 |
||||||||
|
|
|
|
|
|
|
|
|
P5 |
||||||||||
|
|
|
∂y / ∂x2 = 2x2 − x1 +1 = 0. |
|
|
|
|
|
-2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
В |
результате |
получаем |
x1 = −1, |
x2 = −1 |
|
|
-3 |
||||||||||||
(точка P |
|
на рис. 5.2). В ней y = −1. |
|
|
|
|
|
|
P1 |
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
2. Рассматриваем функцию на границах |
|
|
|
||||||||||||||||
области D (см. рис. 5.2): |
|
|
|
|
|
|
|
|
|
|
|
Рис. 5 .2 |
|
||||||
ОВ: x = |
0, |
y = x2 |
+ x |
|
; |
− |
3 ≤ x |
|
≤ 0; |
|
|
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y′x2 = 2x2 +1 = 0, x2 = −1/ 2, y(x2 = −1/ 2) = −1/ 4, |
|
|
|||||||||||||||||
кроме того, |
y(x2 = −3) = 6, |
|
y(x2 = 0) = 0. |
|
|
|
|
|
|
||||||||||
Вывод: на этой границе y |
|
= 6 при ( x |
= 0; |
x |
2 |
= −3) – точка P ; |
|
||||||||||||
|
|
|
|
|
|
sup |
|
|
|
|
1 |
|
|
|
|
1 |
|
||
|
|
|
|
|
|
yinf |
= −1/ 4 при ( x1 = 0; |
|
x2 = −1/ 2 ) – точка P3 . |
||||||||||
ОА: x2 = 0; y = x12 + x1, аналогично получаем
139

|
|
|
ysup = 6 при ( x1 = −3; |
x2 = 0 ) – точка P2 ; |
||||
|
|
|
yinf |
= −1/ 4 при ( x1 = −1/ 2; |
x2 = 0 ) – точка P4 . |
|||
АВ: x |
2 |
= −3 − x ; |
y = 3x2 +9x + 6, |
−3 ≤ x |
|
≤ 0 , аналогично находим: |
||
|
1 |
1 |
1 |
1 |
|
|
||
|
|
|
yinf = −3/ 4 при ( x1 = −3/ 2; |
x2 = −3/ 2) – точка P5 ; |
||||
|
|
|
ysup = 6 в точках P1 и P2 . |
|
||||
Сопоставляя все полученные значения ЦФ, заключаем, что наибольшего значения y = 6 эта функция достигает в угловых точках P1 и P2 области
D, а наименьшее значение y = –1 получается в стационарной точке P0 .
Рассмотренный в данном параграфе материал показывает, что нелинейные задачи оптимизации (как при отсутствии, так и при наличии ограничений) в отдельных случаях допускают аналитическое решение.
Обратимся теперь к следующей задаче. Найти значение x = x *, при котором y = 12 x2 +e−x принимает наименьшее значение.
Наличие решения, совпадающего с локальным минимумом этой довольно простой функции, здесь очевидно. Его отыскание с помощью необходимого условия экстремума приводит к уравнению
y ' = x −e−x = 0, или e−x = x,
которое аналитически невозможно разрешить.
К сожалению, при решении практических задач подобная ситуация, когда необходимое условие экстремума (5.1) приводит к неразрешимой аналитически системе уравнений, довольно типична. Кроме того, нередко встречаются задачи, в которых невозможно получить аналитическое выражение для частных производных от ЦФ. Например, в тех случаях, когда аналитическое выражение для ЦФ отсутствует, а значения ЦФ получаются в результате экспериментов (наблюдений). Во всех подобных случаях для решения оптимизационной задачи приходится использовать численные методы.
§ 5.2. Численные методы решения одномерных задач статической оптимизации
Рассмотрим задачу об отыскании значения переменной x = x*из заданного промежутка [a, b] , при котором ЦФ y = f (x) принимает наи-
меньшее значение. Эта задача минимизации функции одной переменной имеет самостоятельное практическое значение. Кроме того, она нередко возникает как вспомогательная задача при многомерной оптимизации.
140
