
ТФКП индивид.задания.doc Летняя сессия 2015г
.docИндивидуальные задания
индивидуальные задания по тфкп
-
Исследовать функцию на аналитичность.
-
Проверить, является ли функция гармонической. Если да, то по ней восстановить аналитическую функцию
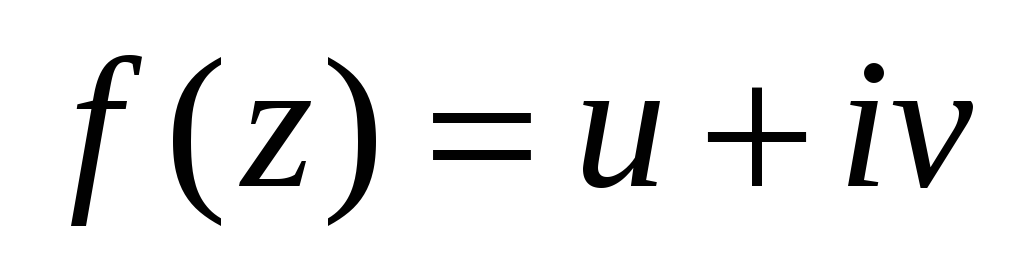 .
. -
Задание на дробно-линейную функцию.
-
Вычислить интеграл функции комплексного переменного.
5,6. Вычислить интегралы, используя интегральную теорему, формулу Коши или интегральное представление для производных.
-
Разложить функцию в ряд Тейлора, пользуясь известными разложениями для элементарных функций. Указать круг сходимости.
-
Найти радиус и круг сходимости степенного ряда.
-
Разложить функцию в ряд Лорана в указанной области.
-
Разложить функцию в ряд Лорана в окрестности
 .
. -
Найти особые точки функции и установить их тип.
-
Найти вычеты во всех изолированных особых точках.
-
Вычислить интеграл, используя интегральную теорему Коши о вычетах.
-
Вычислить значение элементарной функции.
ВАРИАНТ №1
-
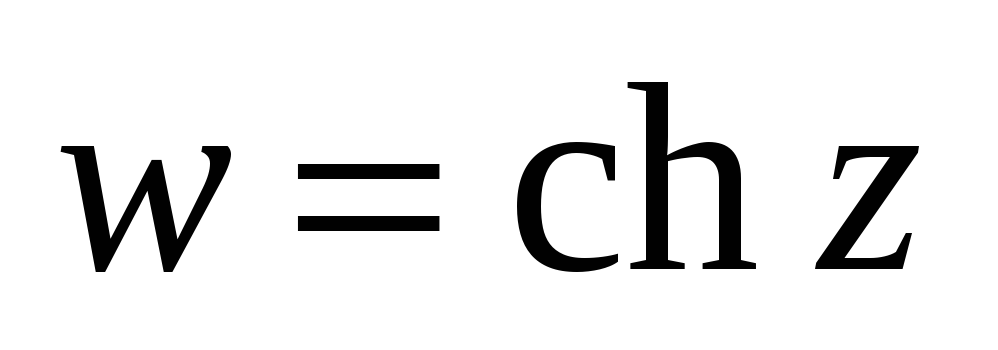
-
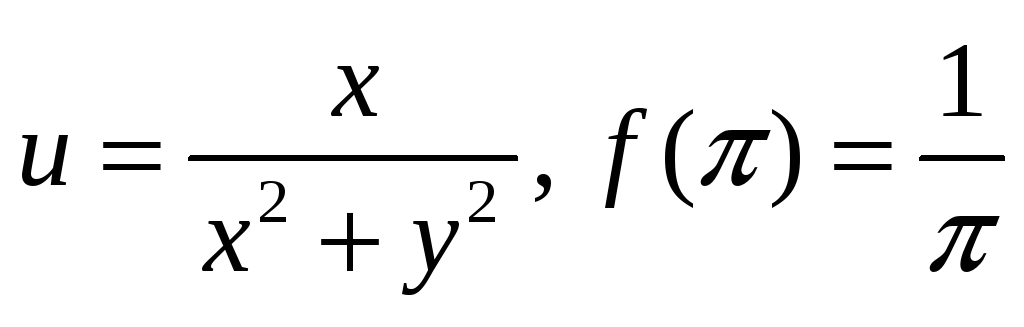
-
Найти дробно-линейную функцию, отображающую точки
 в точки
в точки
 соответственно. Во что при этом
отобразится круг
соответственно. Во что при этом
отобразится круг
 ?
? -
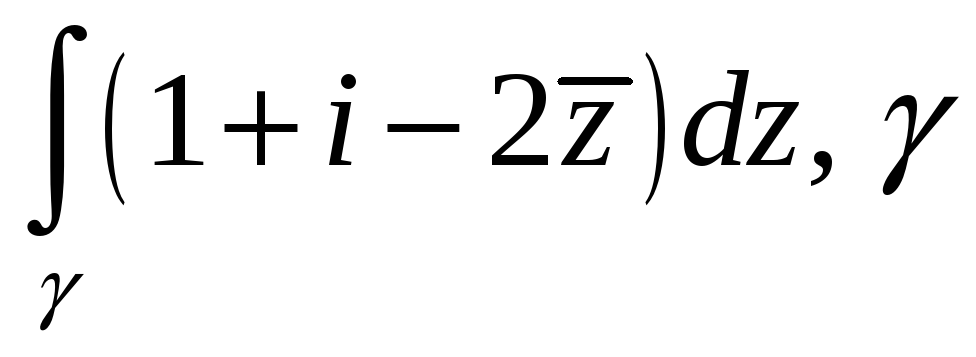 -
прямая от
-
прямая от
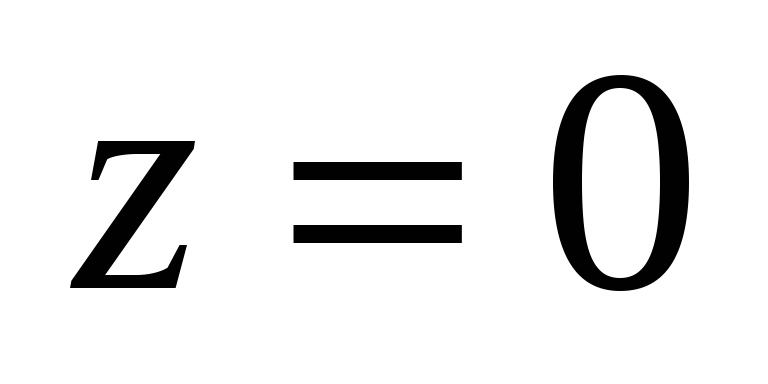 до
до
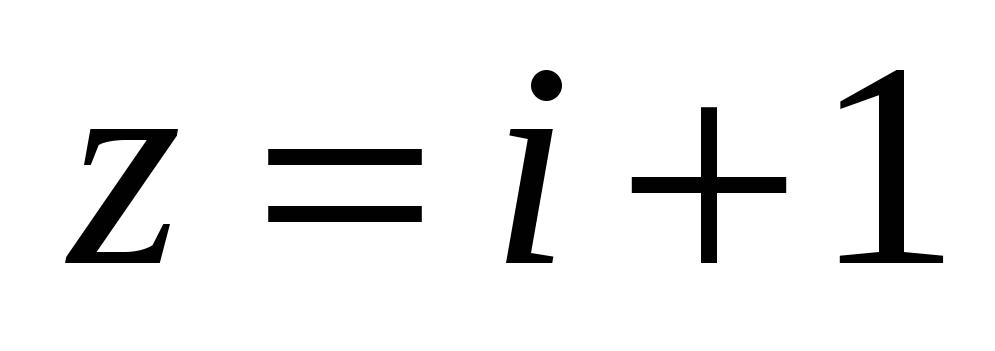
-
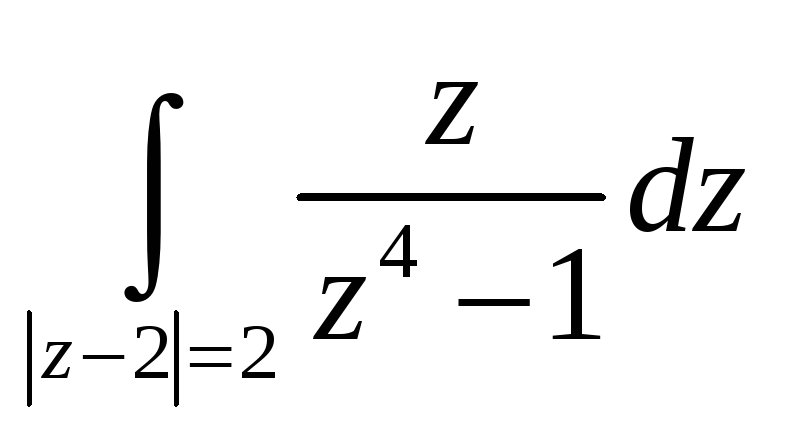
-
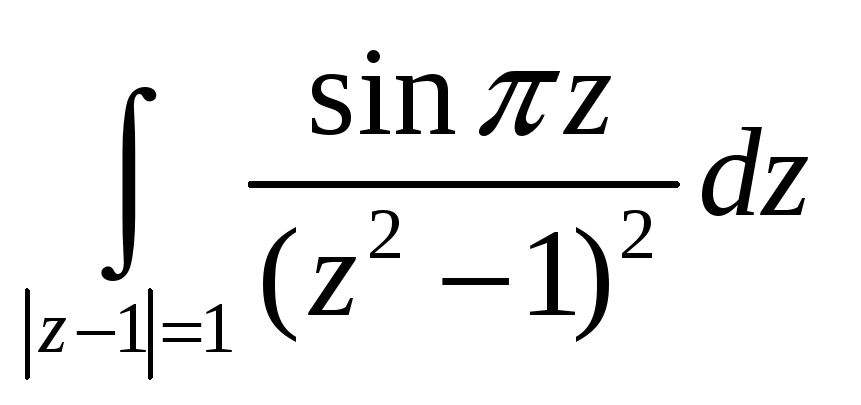
-
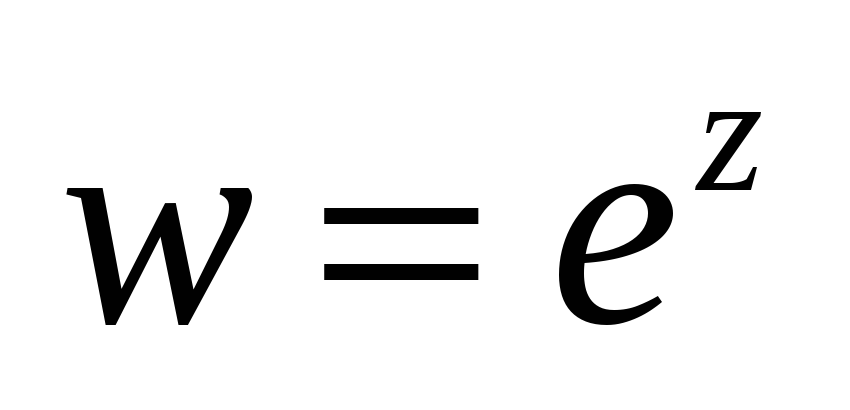 в
окрестности
в
окрестности
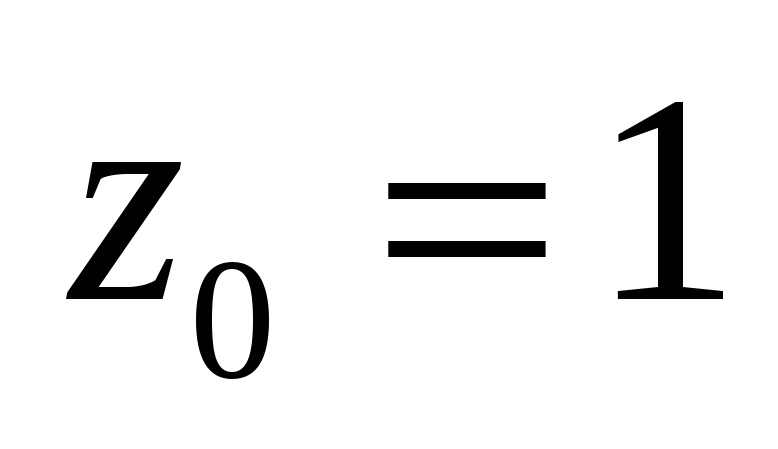
-

-
 в
в
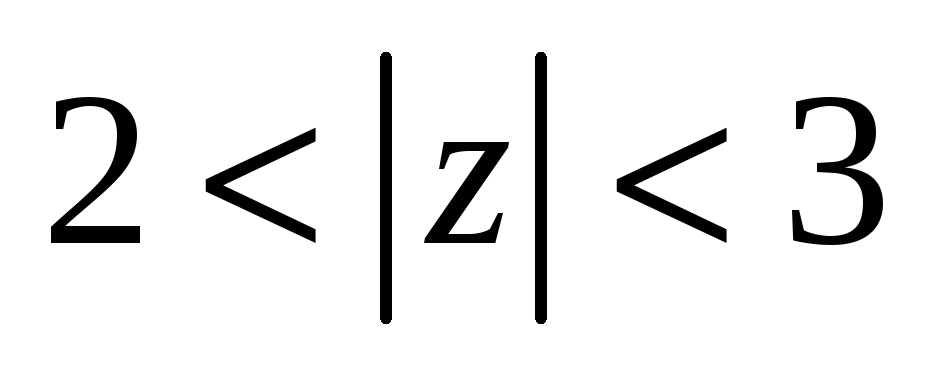
-

-

-

-

-
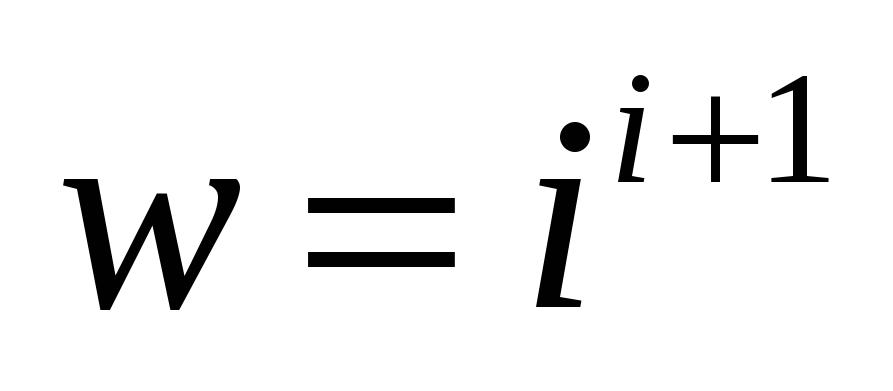
ВАРИАНТ №2
-
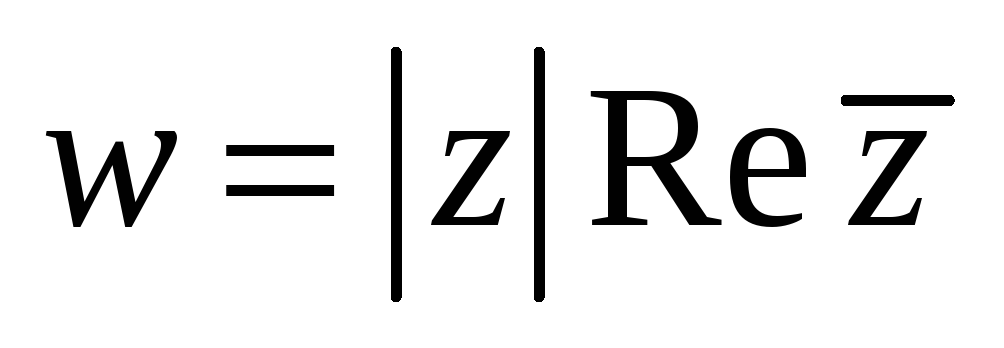
-
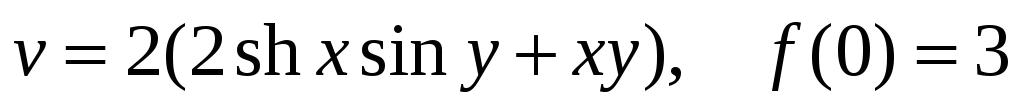
-
Найти дробно-линейную функцию, отображающую круг
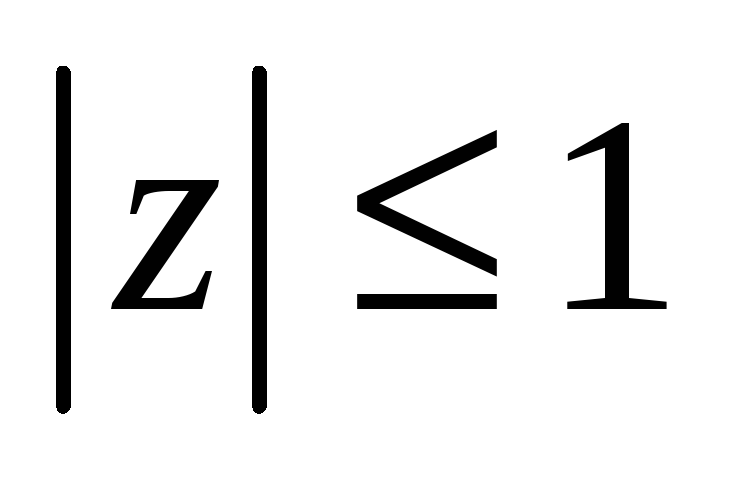 в себя так, что точка
в себя так, что точка
 отображается
в 0, а точка
отображается
в 0, а точка
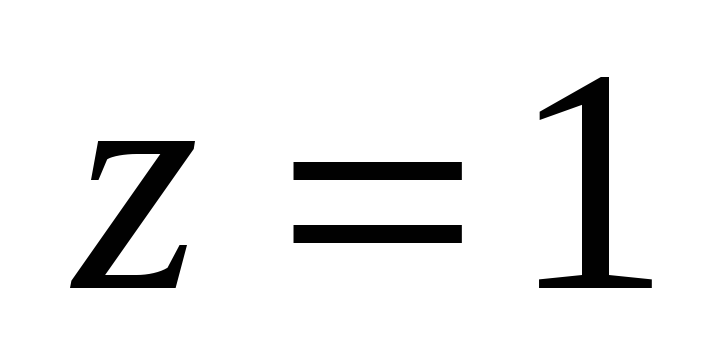 - в
- в
 .
. -

-

-
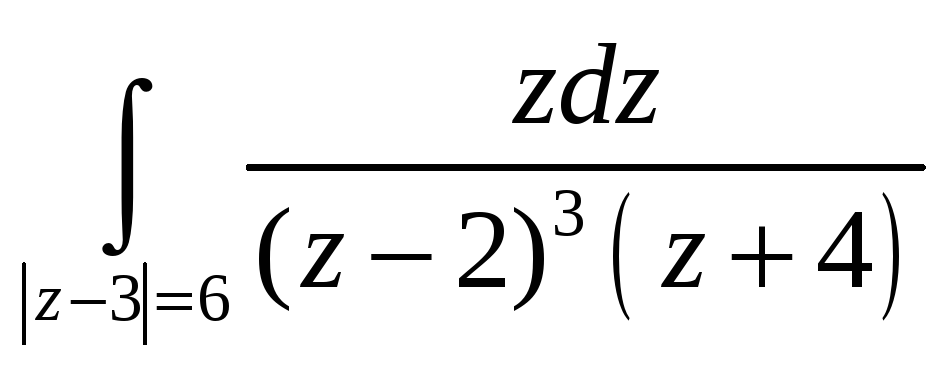
-
 в
окрестности
в
окрестности
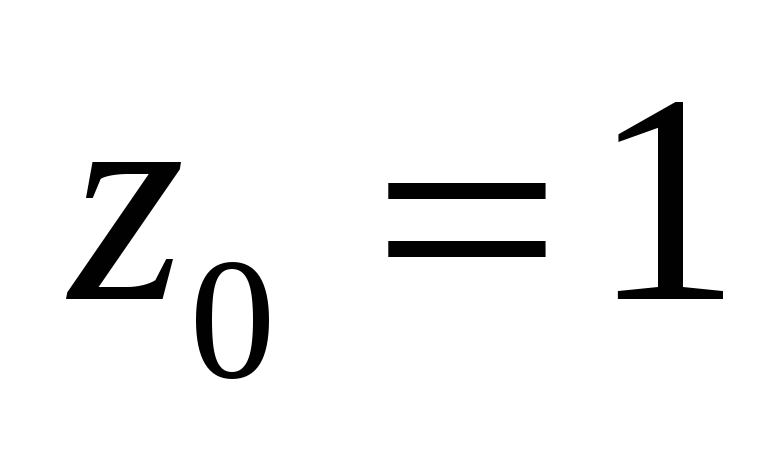
-
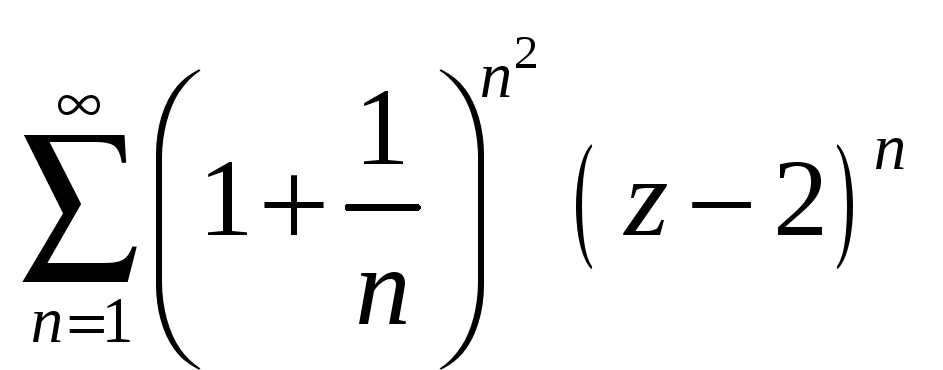
-
 в
в

-

-

-

-

-

ВАРИАНТ №3
-
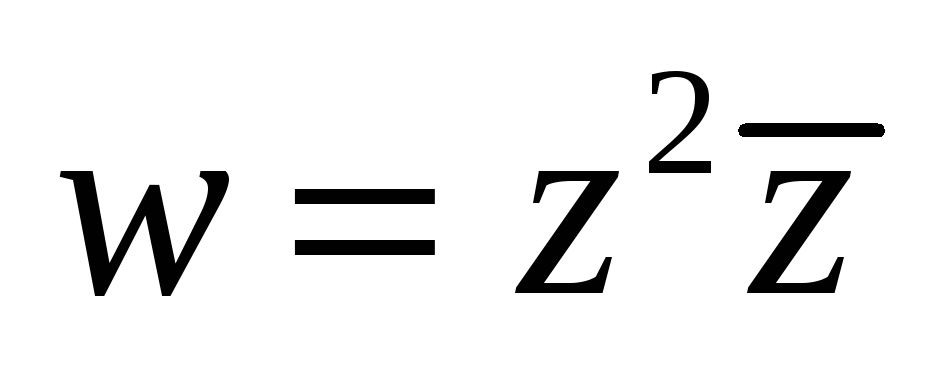
-
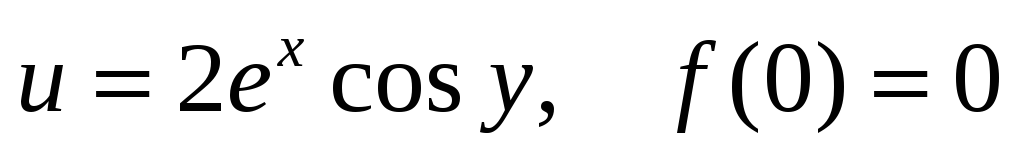
-
Найти дробно-линейную функцию, отображающую точки
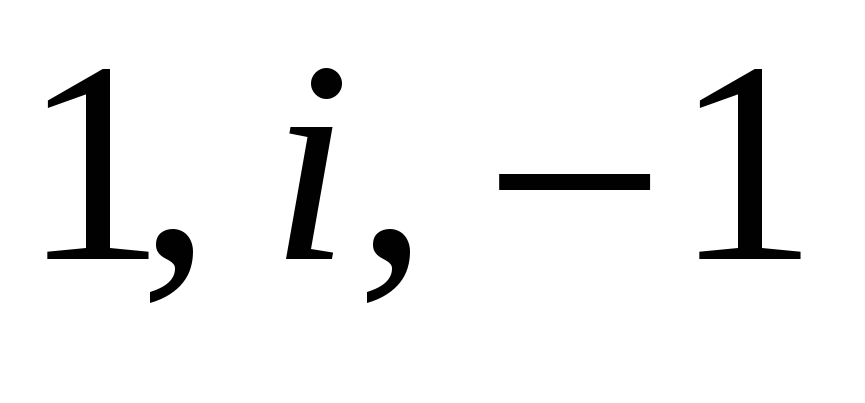 в точки
в точки
 соответственно. Во что при этом
отобразится единичный круг?
соответственно. Во что при этом
отобразится единичный круг? -
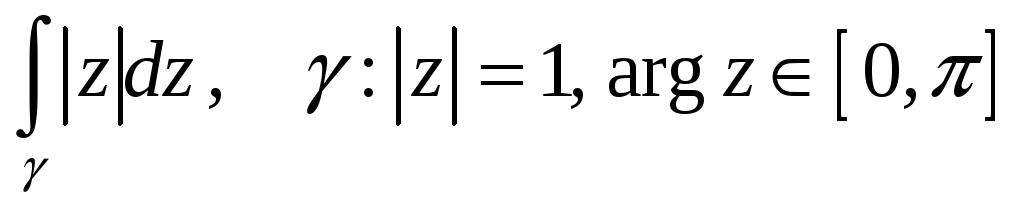
-
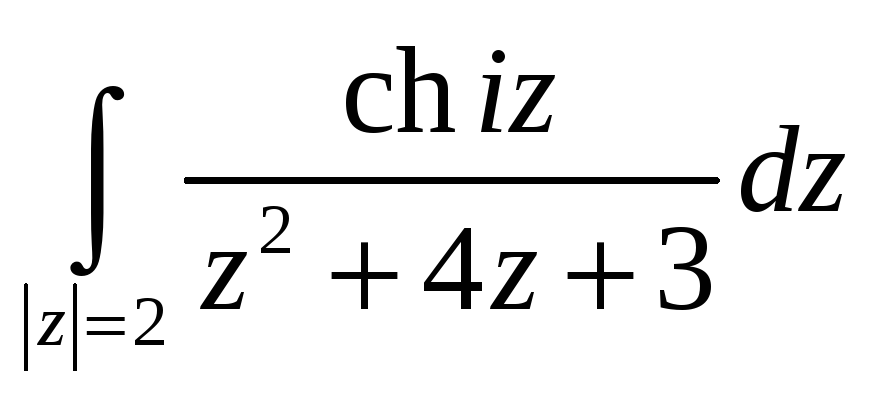
-
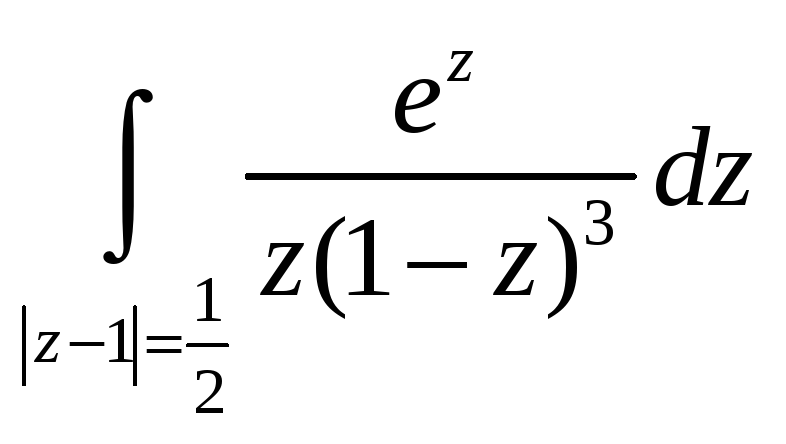
-
 в
окрестности
в
окрестности
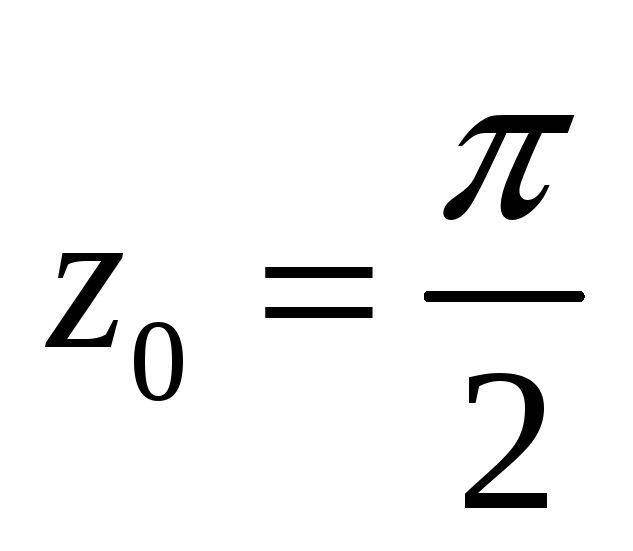
-
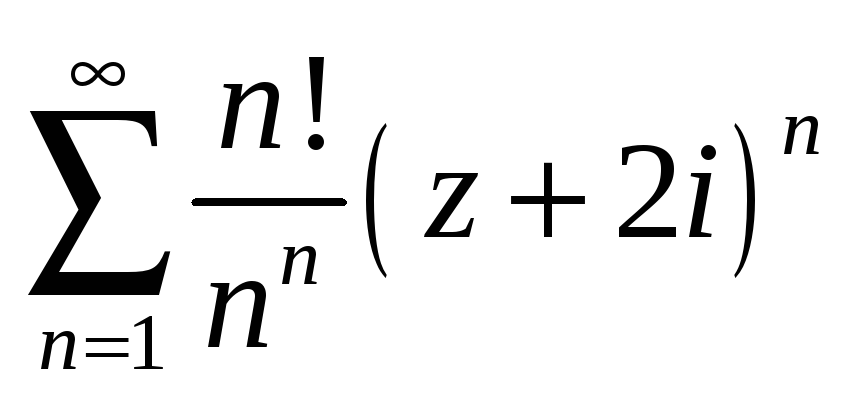
-
 в
кольце
в
кольце
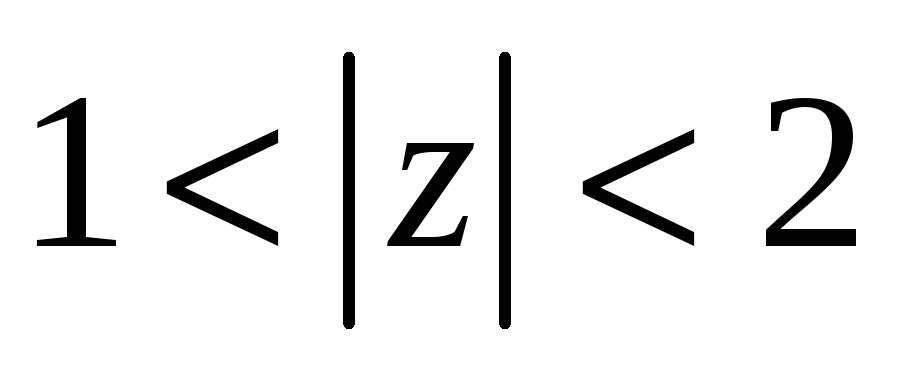
-
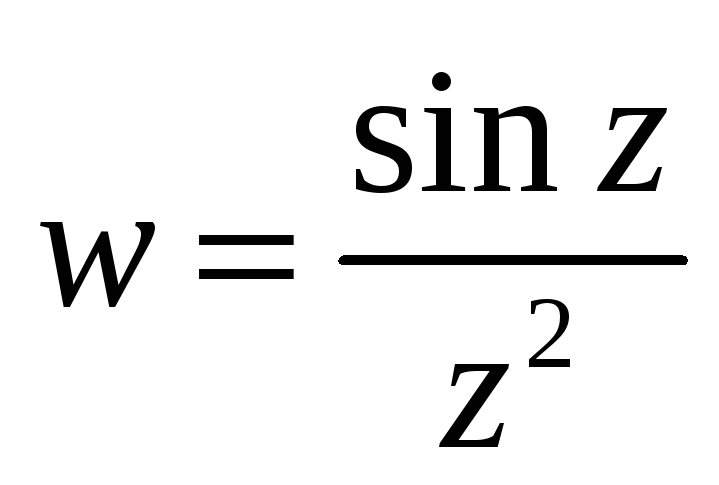
-

-

-

-
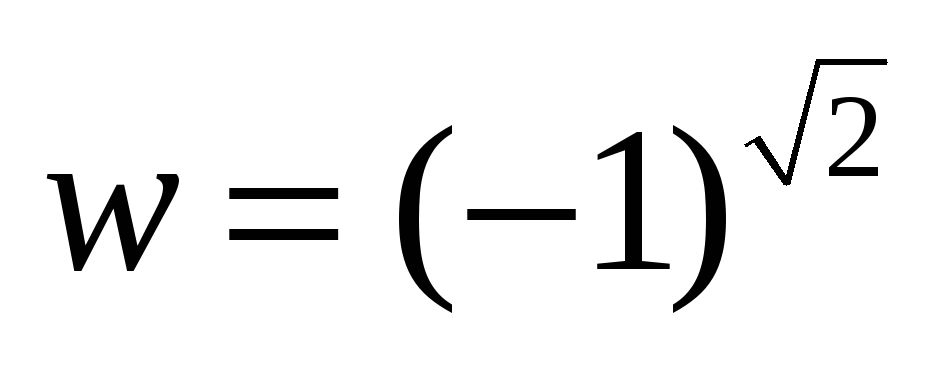
ВАРИАНТ №4
-

-

-
Найти дробно-линейную функцию, отображающую
 на
на
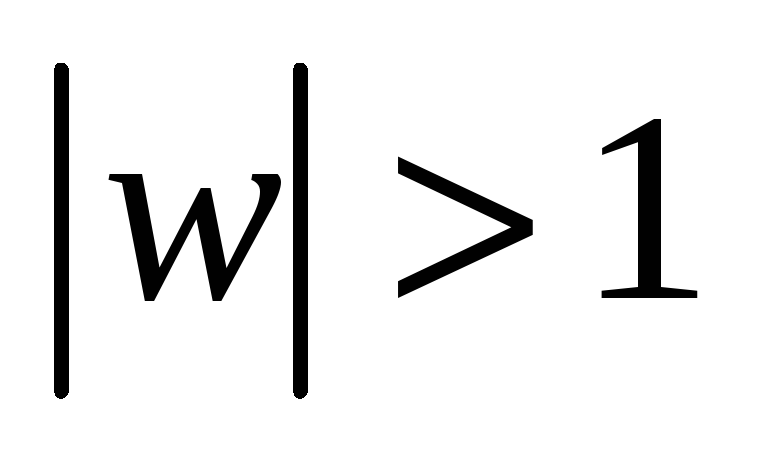 так, чтобы точки
так, чтобы точки
 перешли
в
перешли
в
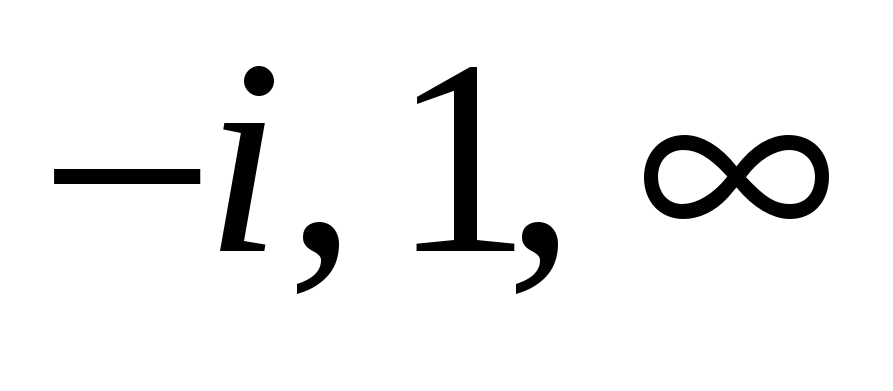 соответственно.
соответственно. -
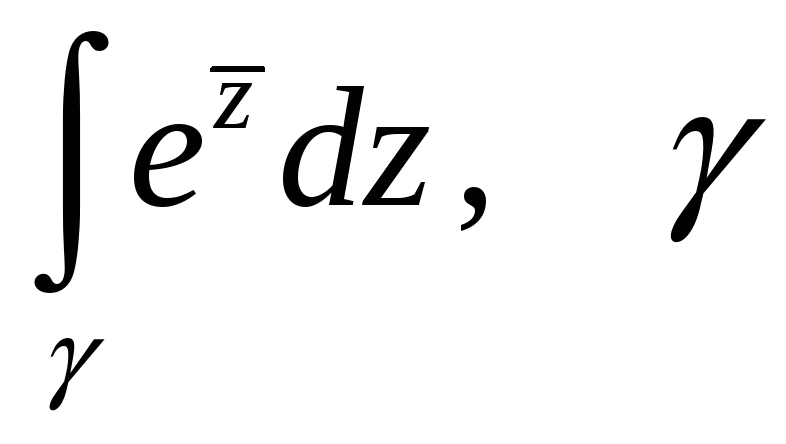 -
отрезок прямой
-
отрезок прямой
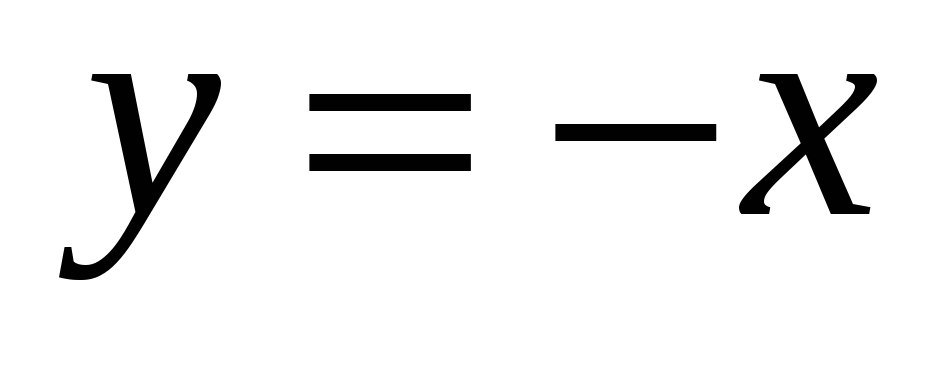 от
0 до
от
0 до

-
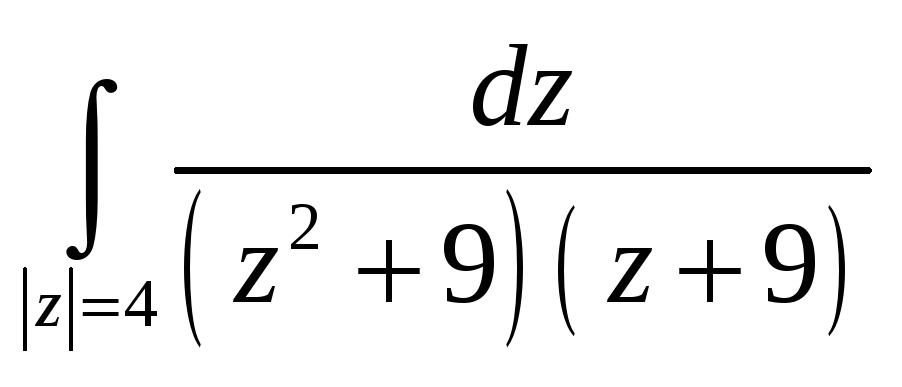
-
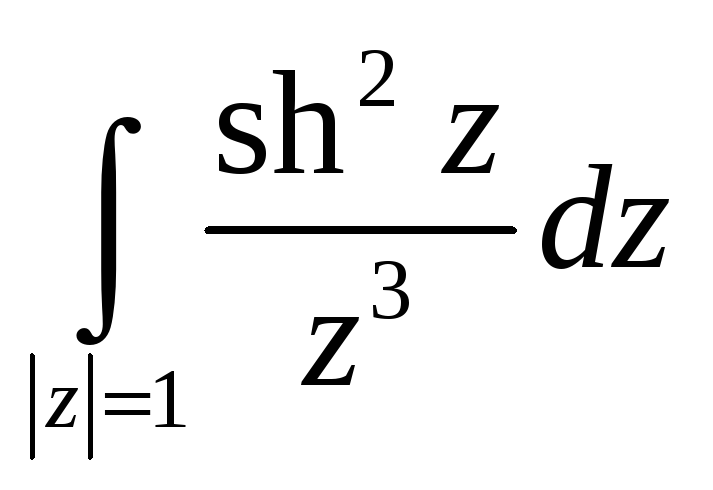
-
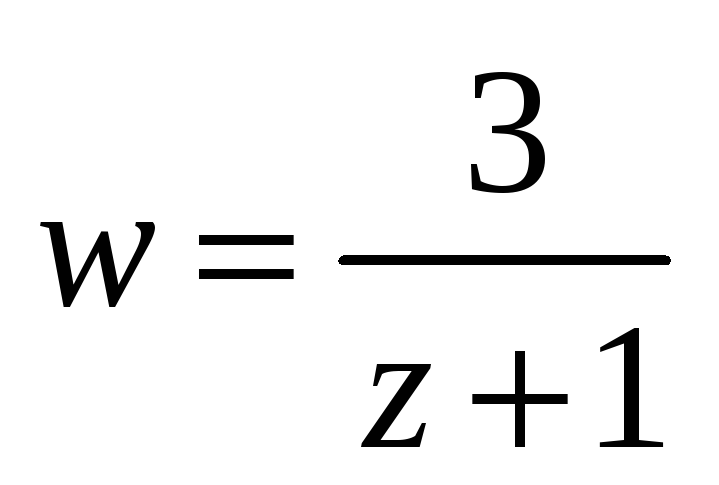 в
окрестности
в
окрестности

-
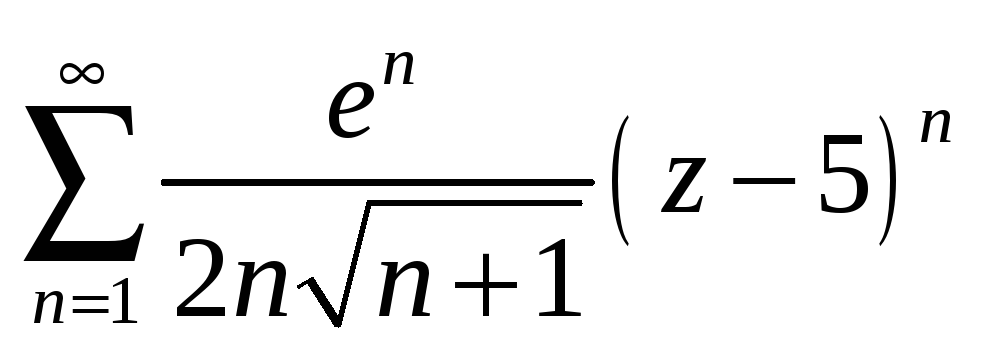
-
 в
в
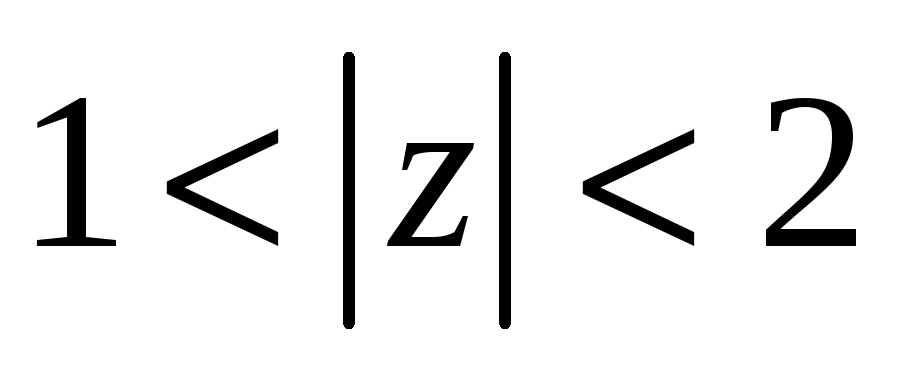
-

-

-
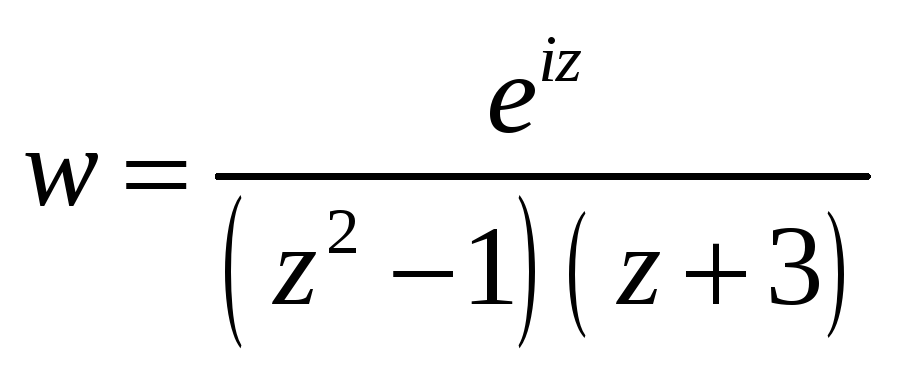
-

-

ВАРИАНТ №5
-
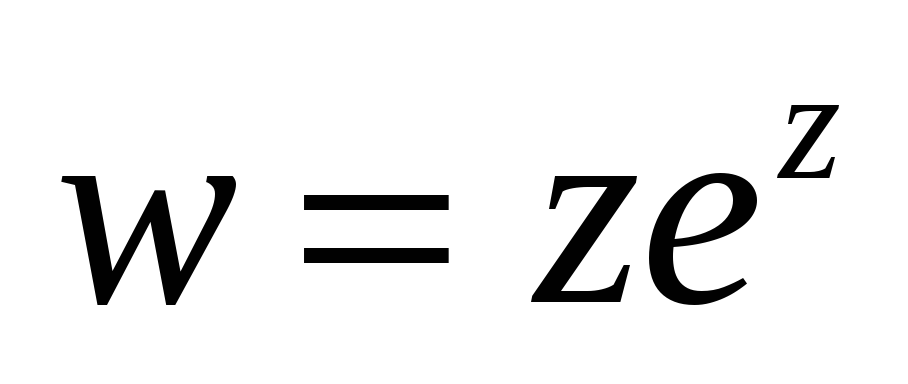
-

-
Найти дробно-линейную функцию, отображающую круг
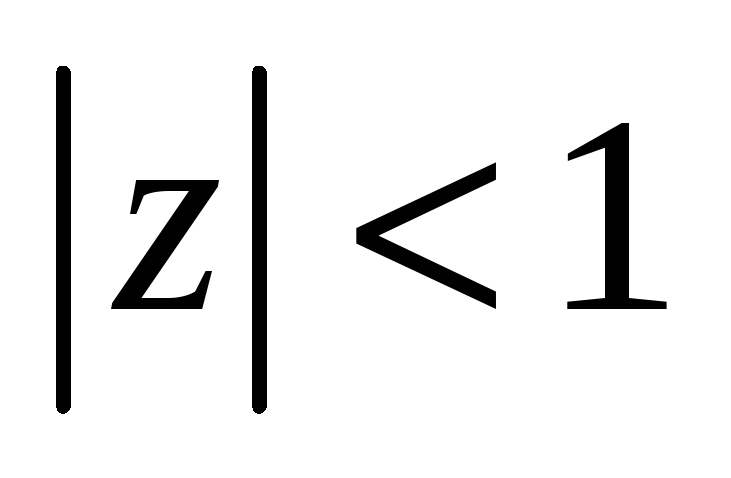 на полуплоскость
на полуплоскость
 так, чтобы точки
так, чтобы точки
 перешли в
перешли в
 соответственно.
соответственно. -
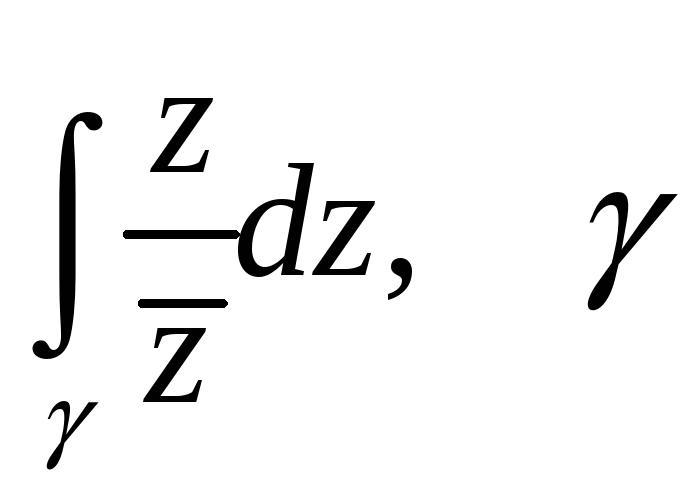 -
граница полукольца
-
граница полукольца
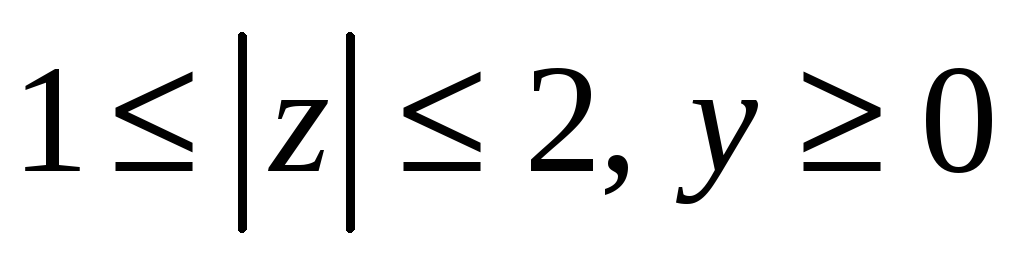
-
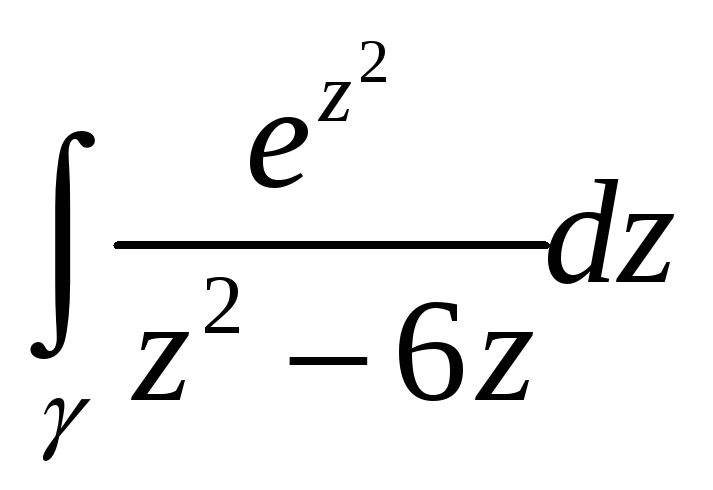 ,
,

-
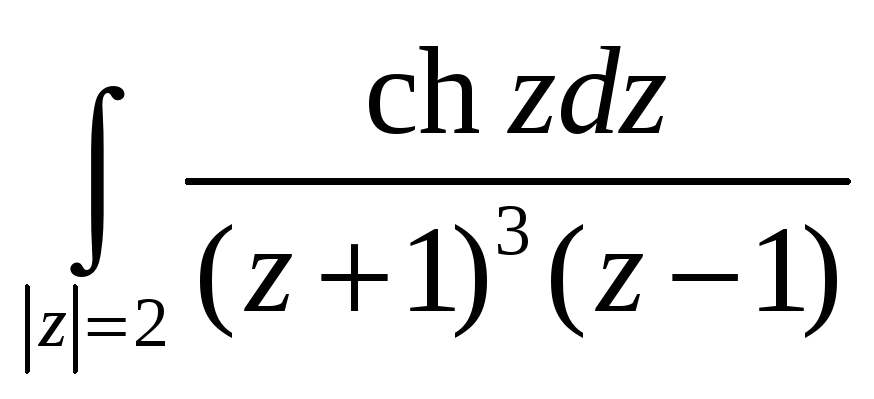
-
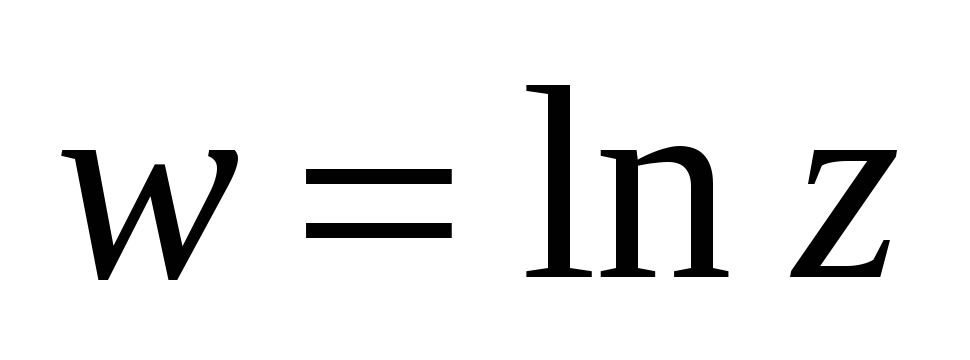 в
окрестности
в
окрестности
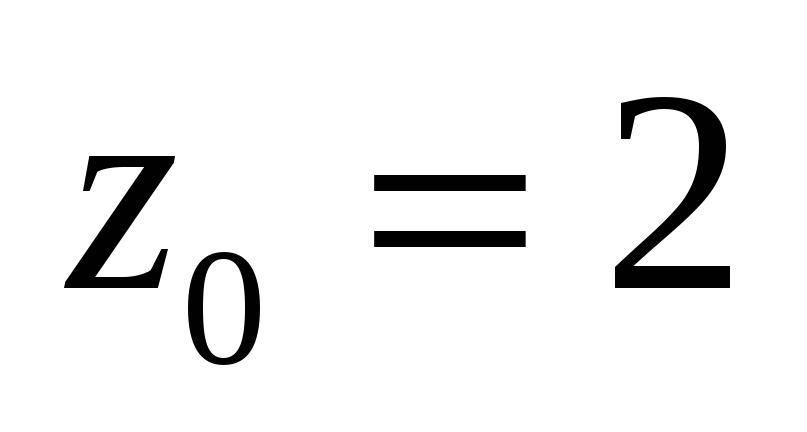
-
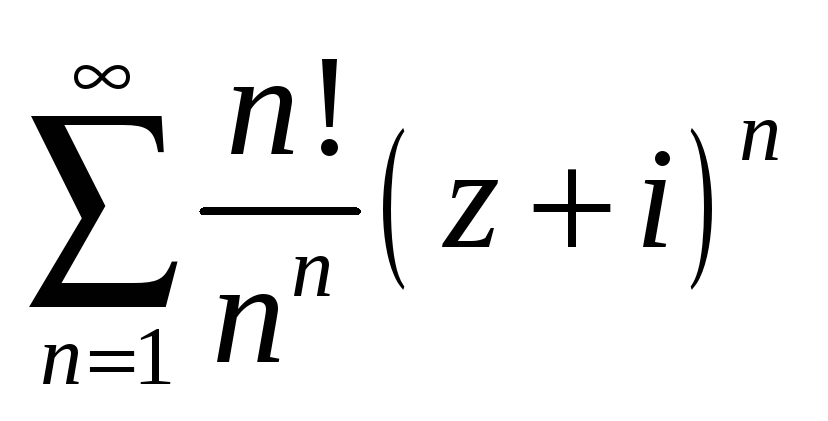
-
 в
в
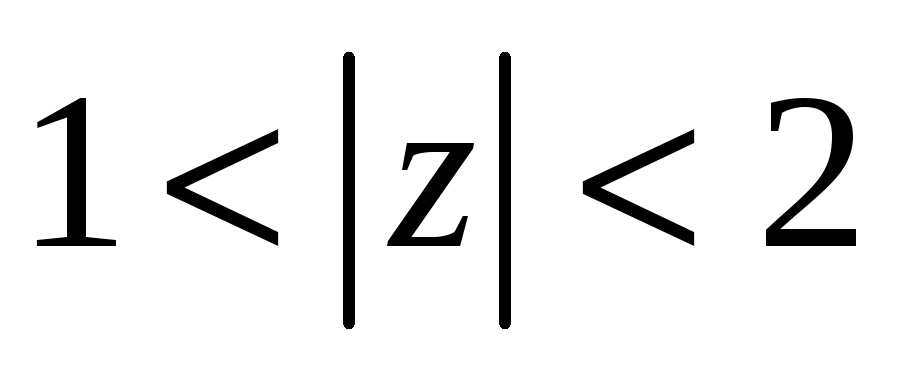
-
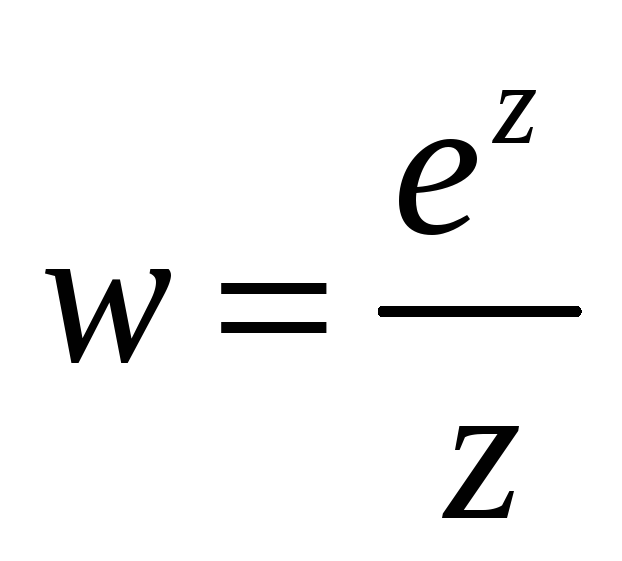
-

-

-

-
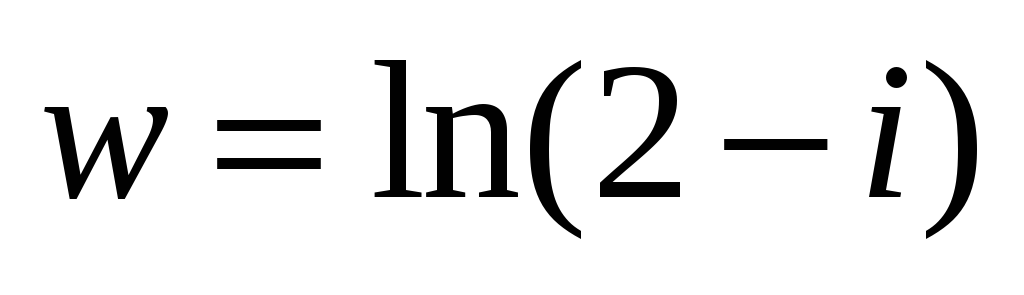
ВАРИАНТ №6
-

-

-
Найти дробно-линейную функцию, отображающую точки
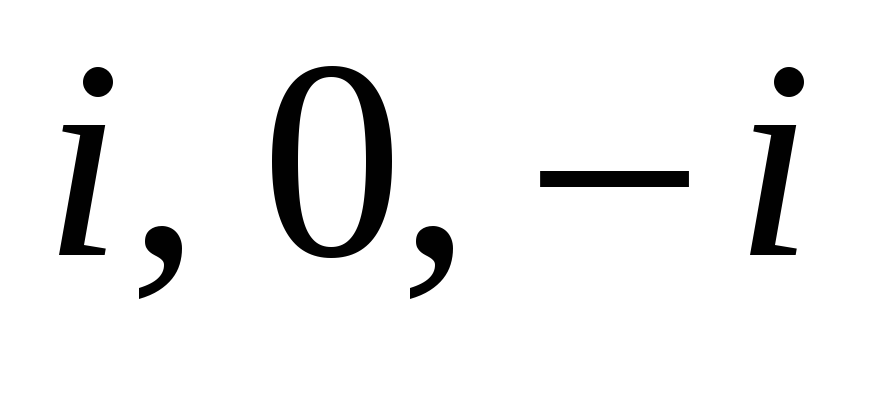 в точки
в точки
 соответственно. В какую область
отобразится при этом полуплоскость
соответственно. В какую область
отобразится при этом полуплоскость
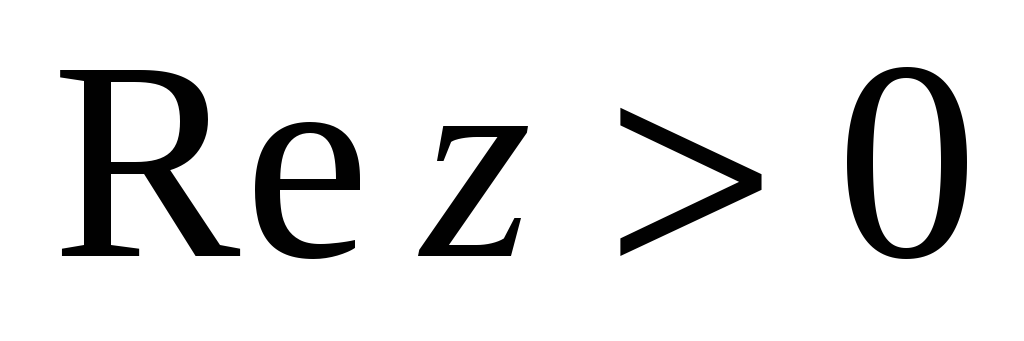 ?
? -

-

-

-
 в
окрестности
в
окрестности

-
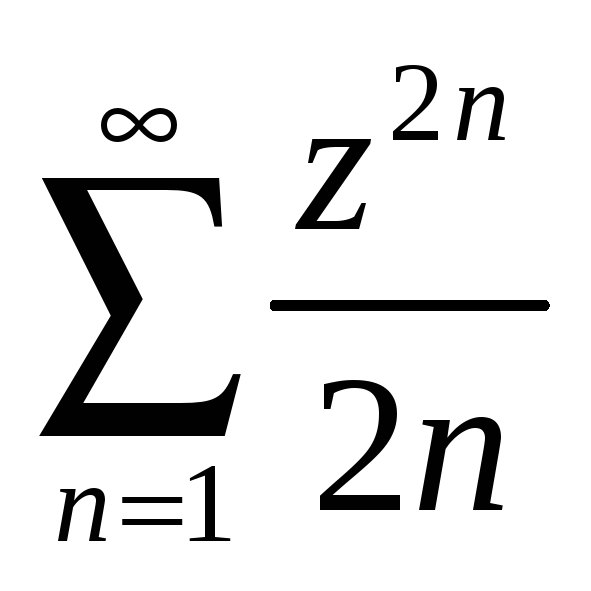
-
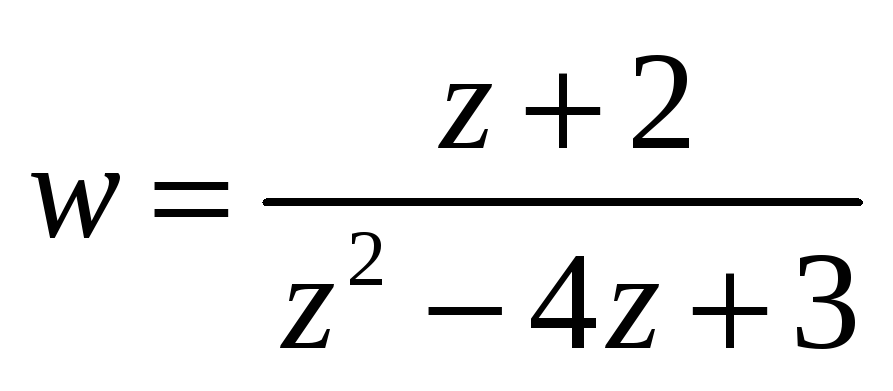 в
в
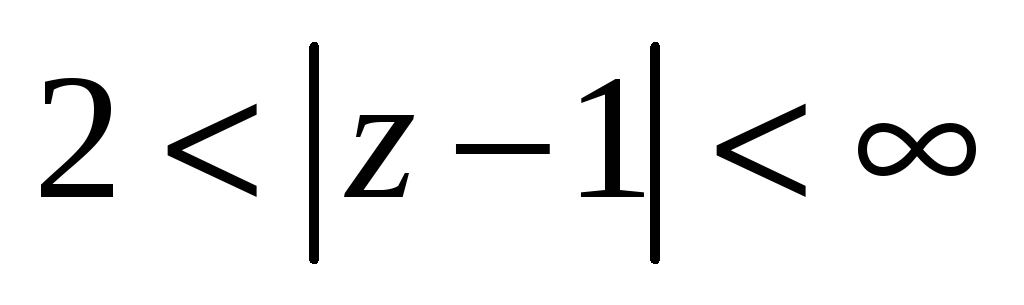
-

-

-

-

-
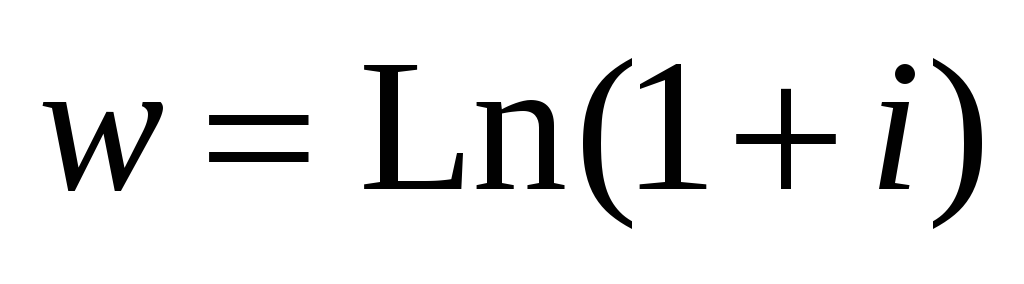
ВАРИАНТ №7
-
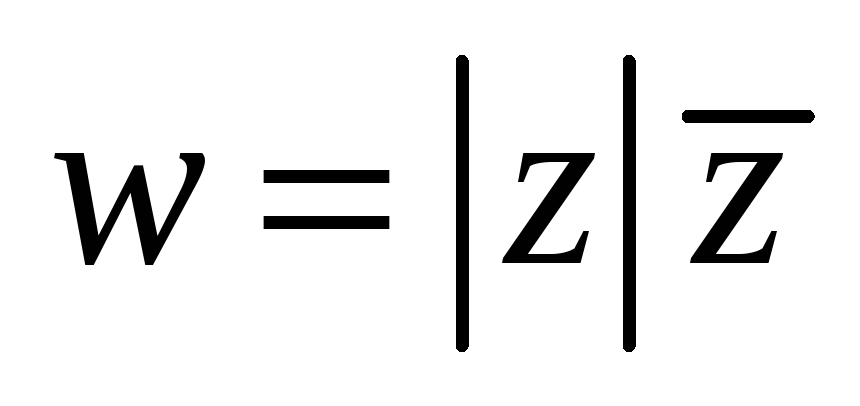
-
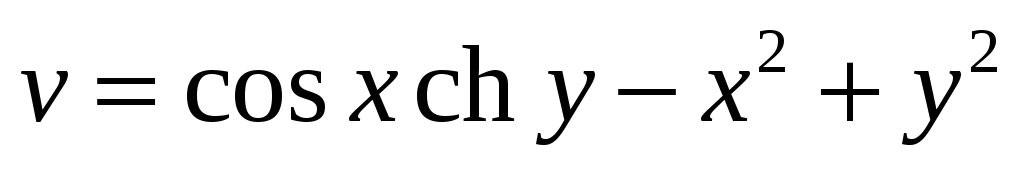
-
Найти дробно-линейную функцию, отображающую круг
 на круг
на круг
 так, чтобы точки
так, чтобы точки
 перешли в точки
перешли в точки
 соответственно.
соответственно. -
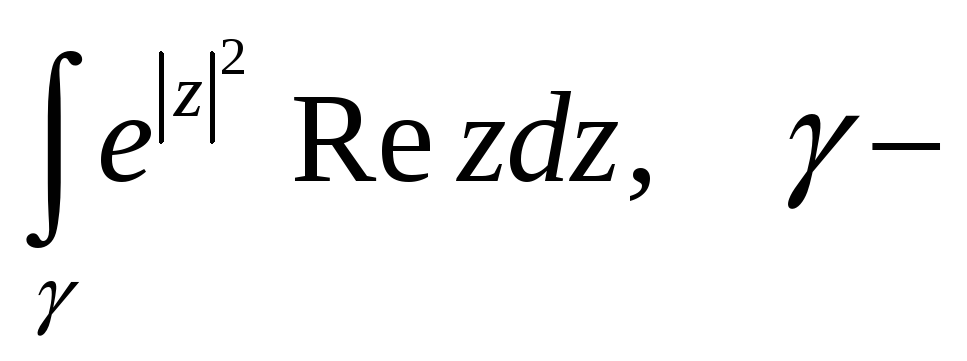 отрезок
прямой от 0 до
отрезок
прямой от 0 до
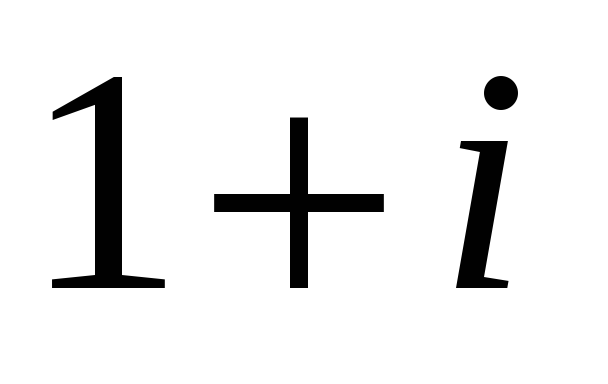
-
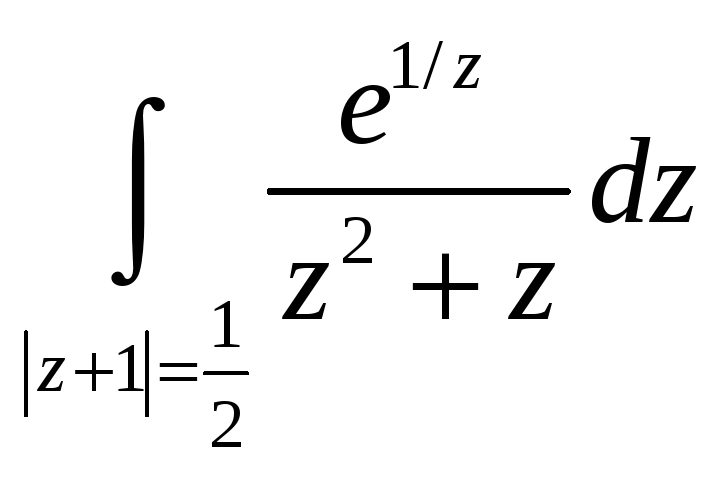
-
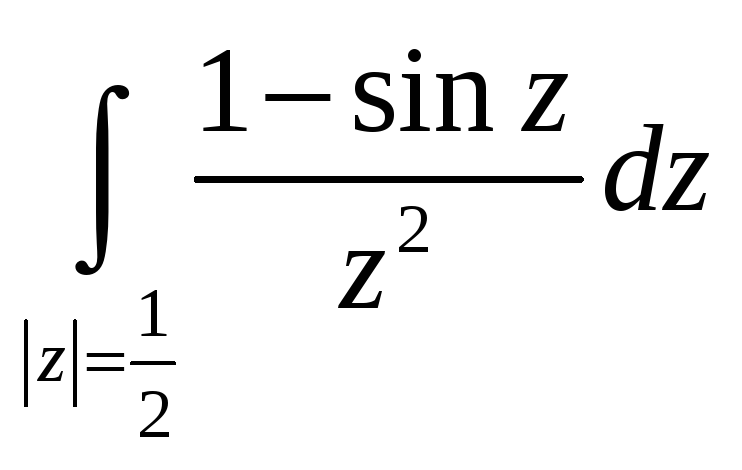
-
 в
окрестности
в
окрестности

-
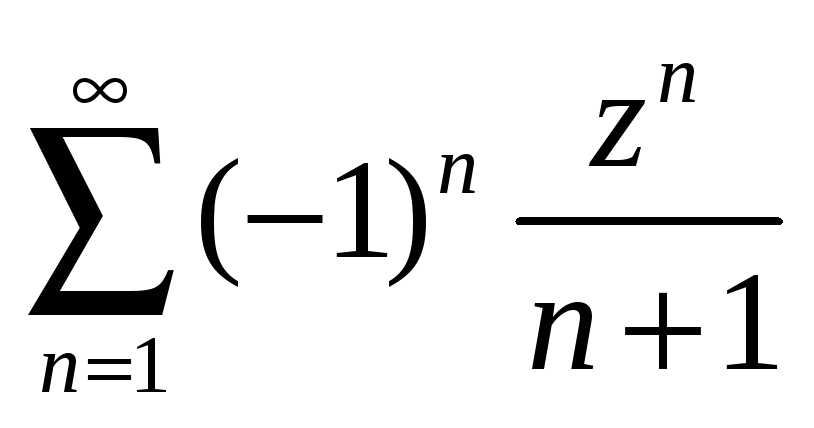
-

-

-
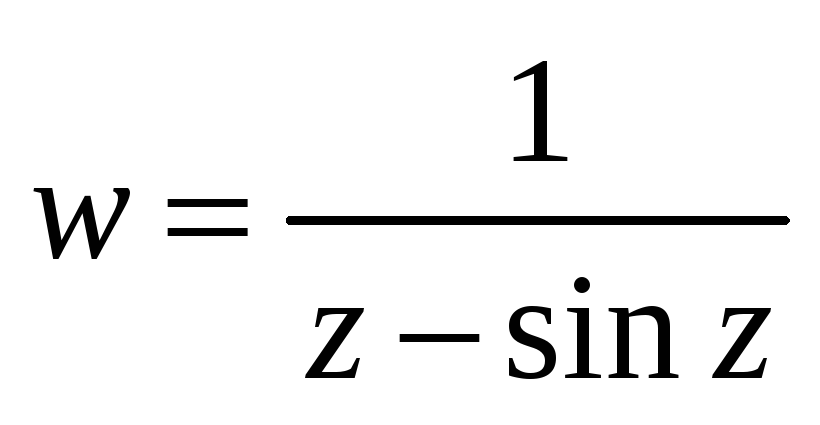
-
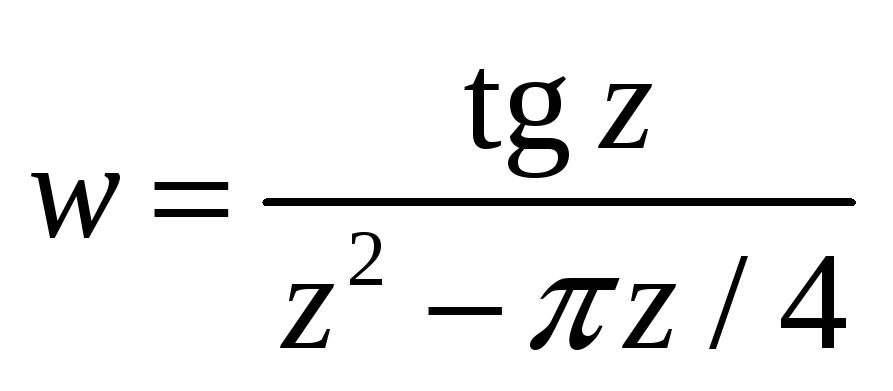
-

-
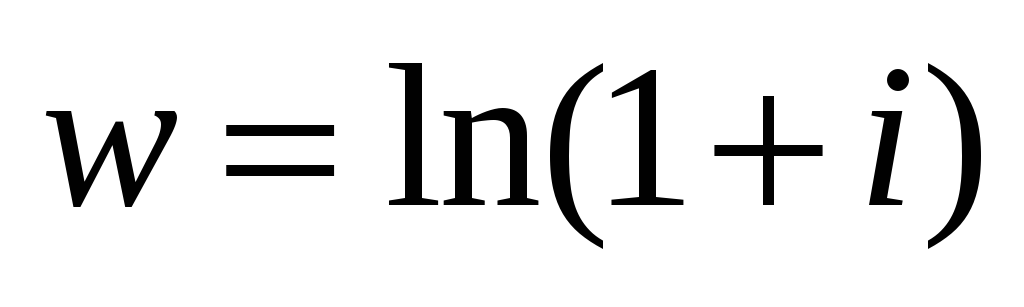
ВАРИАНТ №8
-

-

-
Найти дробно-линейную функцию, отображающую
 на
на
 так, чтобы точка
так, чтобы точка
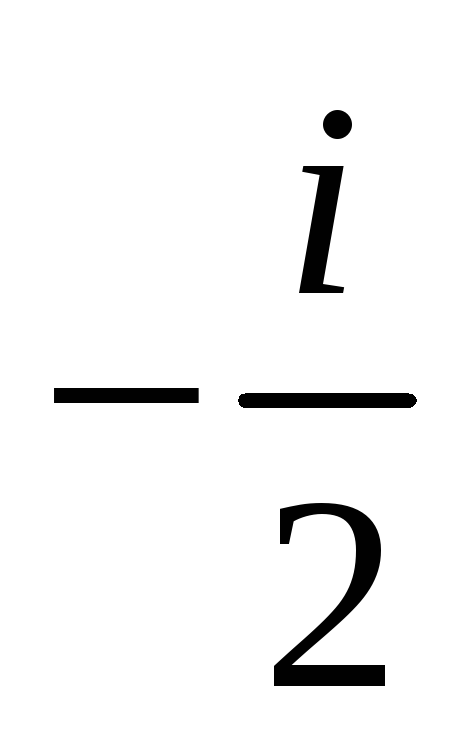 перешла в 0, а точка
перешла в 0, а точка
 - в 2.
- в 2. -

-

-
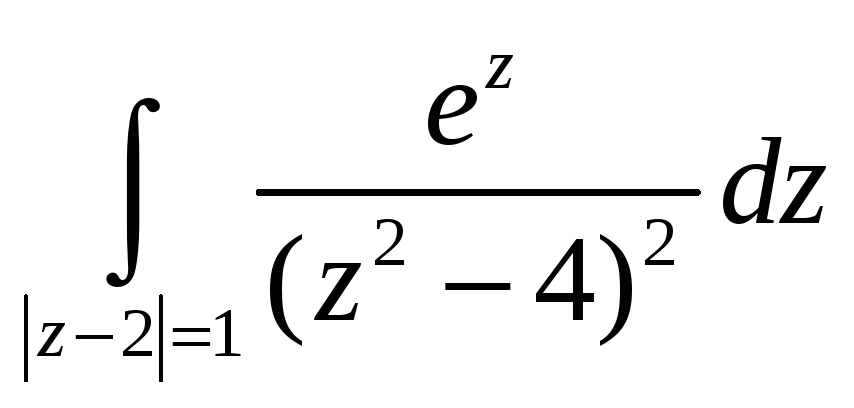
-
 в
окрестности
в
окрестности

-

-
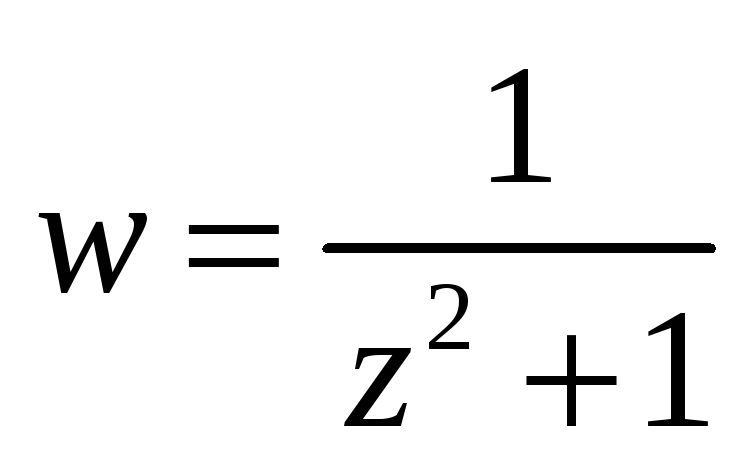 в
в

-

-
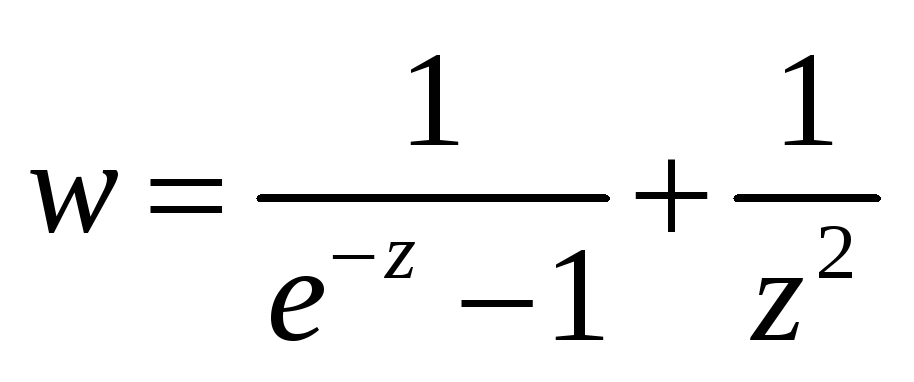
-

-

-
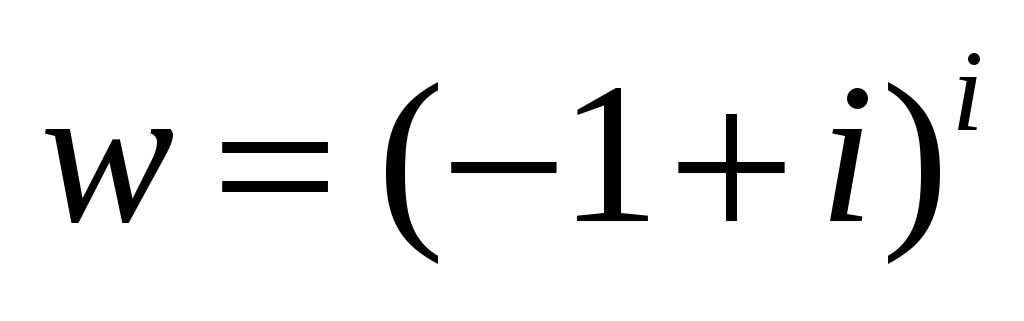
ВАРИАНТ №9
-

-
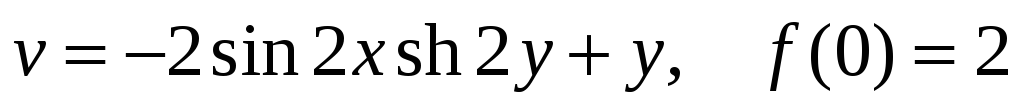
-
Найти дробно-линейную функцию, отображающую круг
 на круг
на круг
 так, чтобы точки
так, чтобы точки
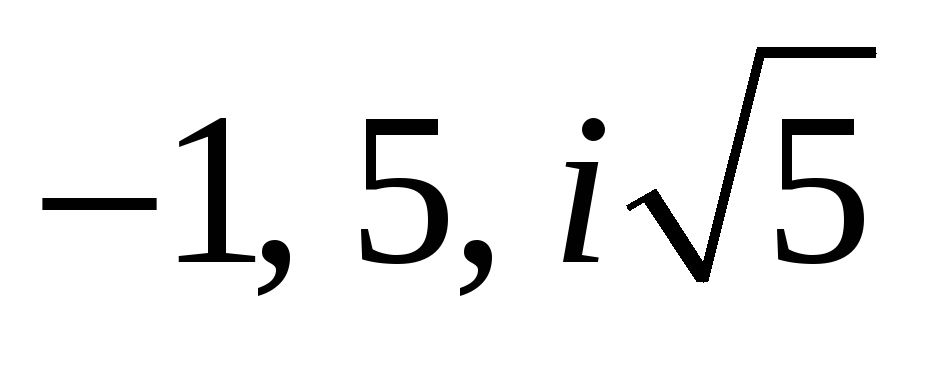 перешли в точки
перешли в точки
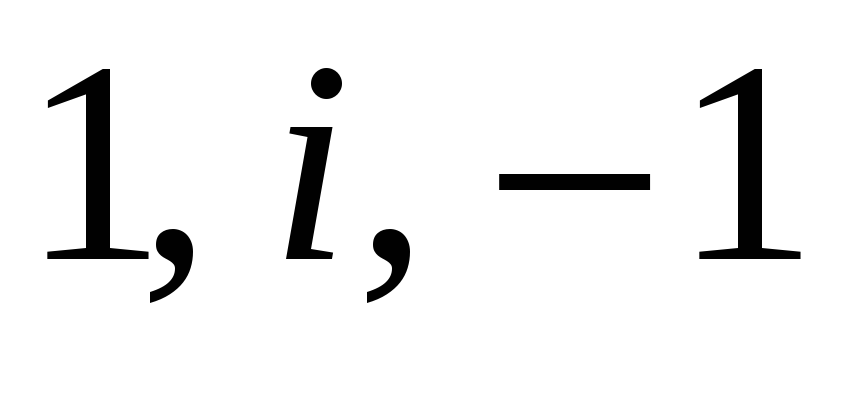 соответственно.
соответственно. -
 ломаная,
состоящая из
ломаная,
состоящая из
 и отрезка от 2 до
и отрезка от 2 до
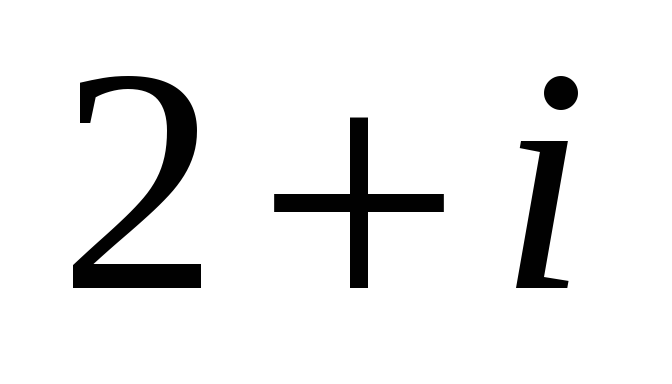
-
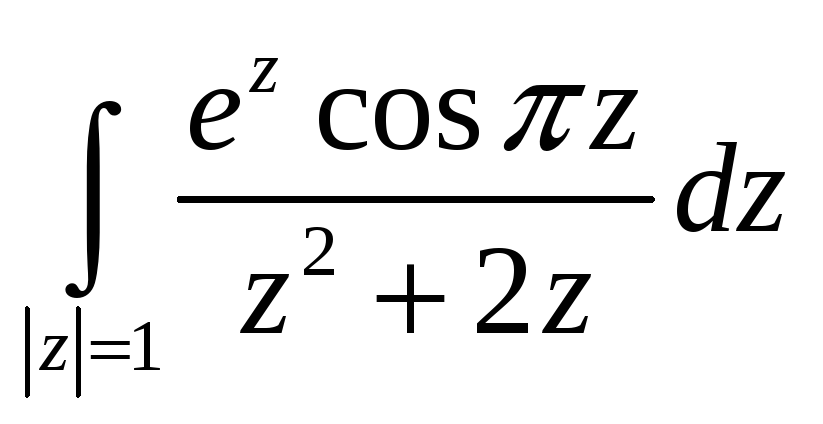
-

-
 в
окрестности
в
окрестности

-
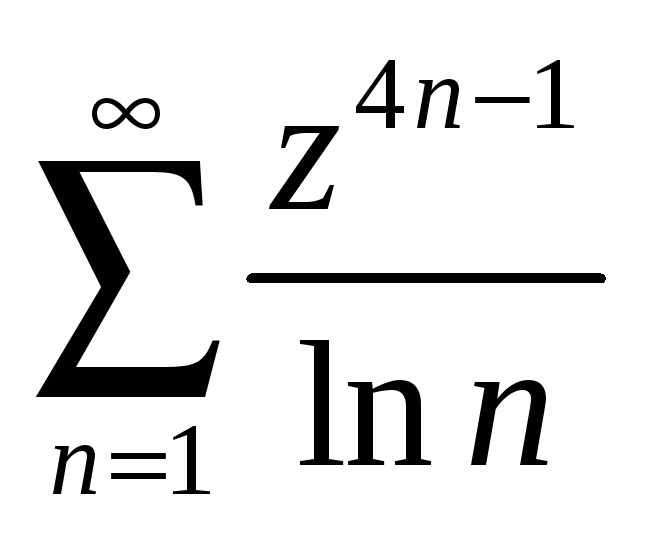
-
 в
в
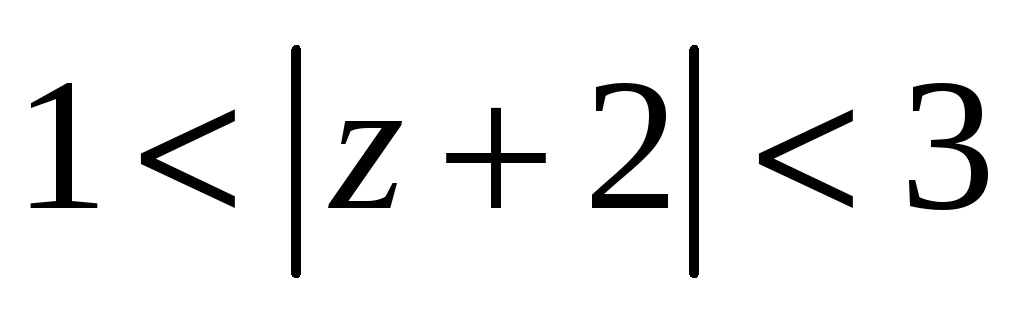
-
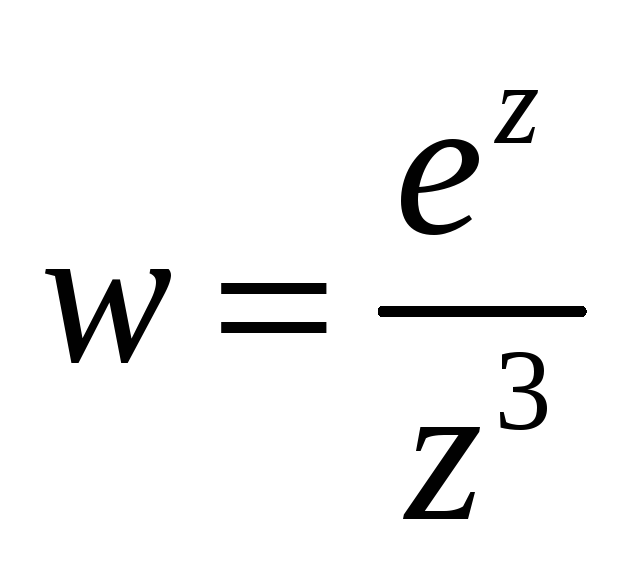
-

-
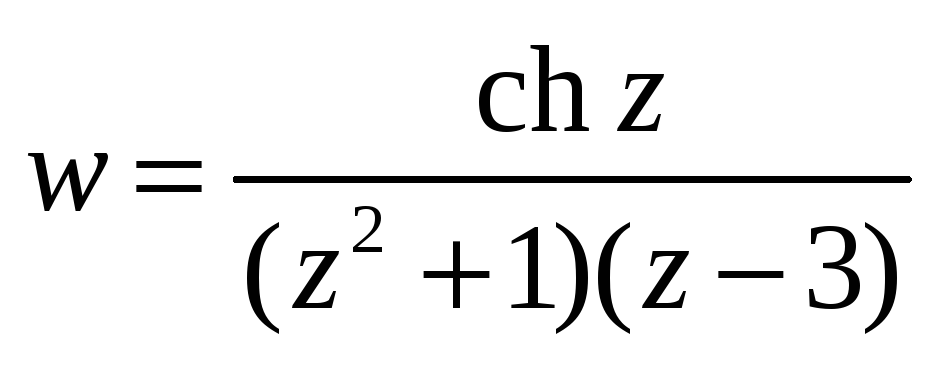
-

-

ВАРИАНТ №10
-
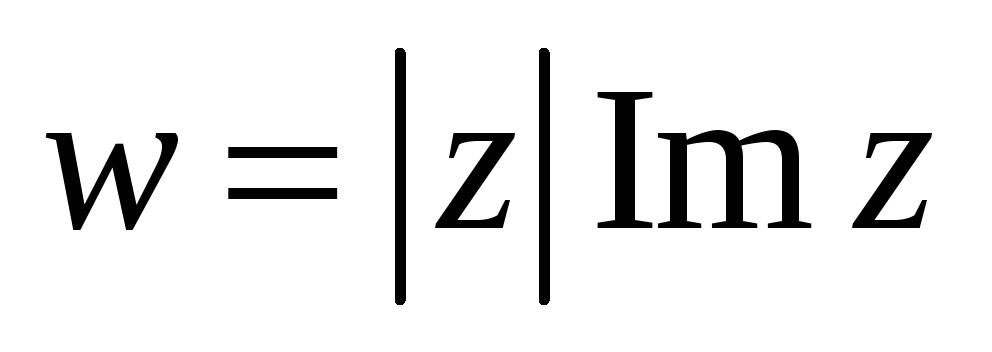
-
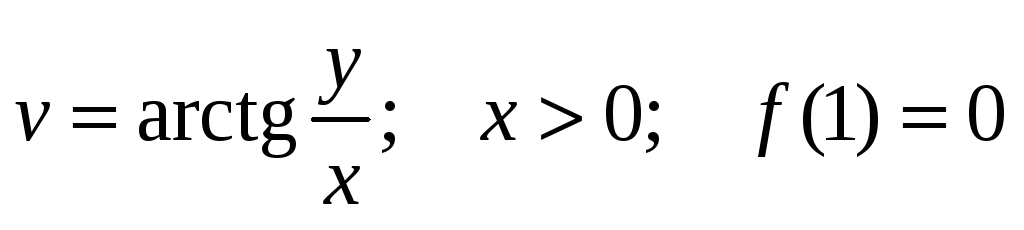
-
Найти дробно-линейную функцию, отображающую точки
 в точки
в точки
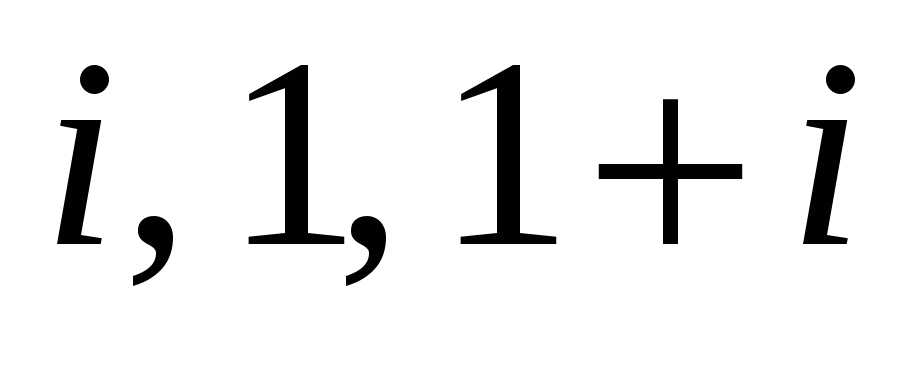 соответственно. Во что при этом
отобразится верхняя полуплоскость?
соответственно. Во что при этом
отобразится верхняя полуплоскость? -
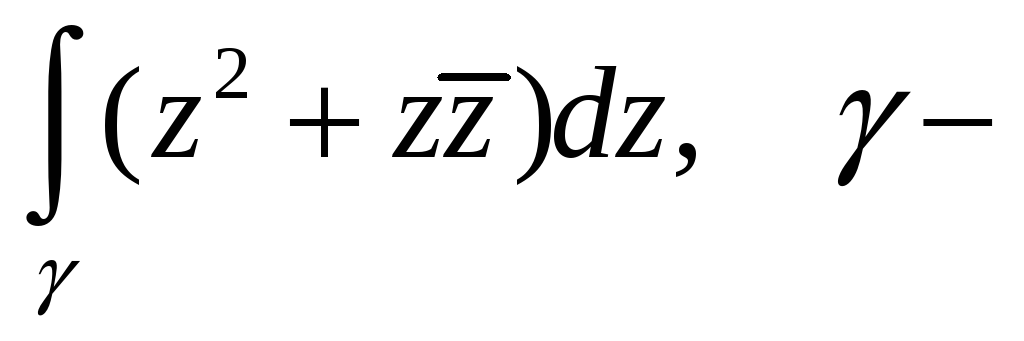 дуга
окружности
дуга
окружности
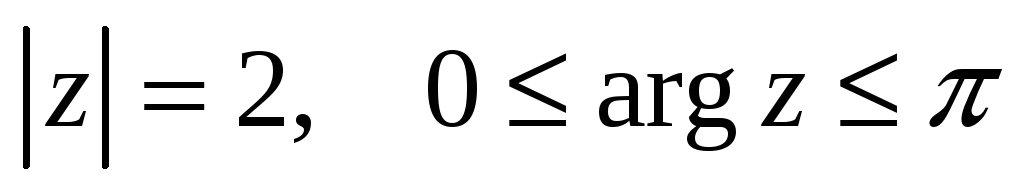
-

-
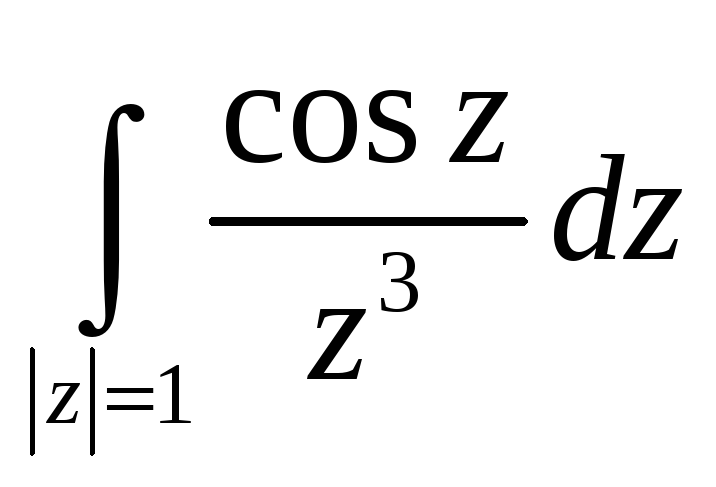
-
 в
окрестности
в
окрестности
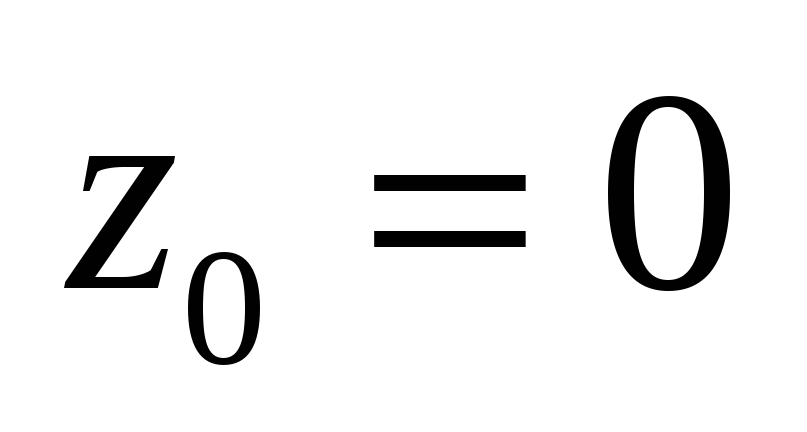
-
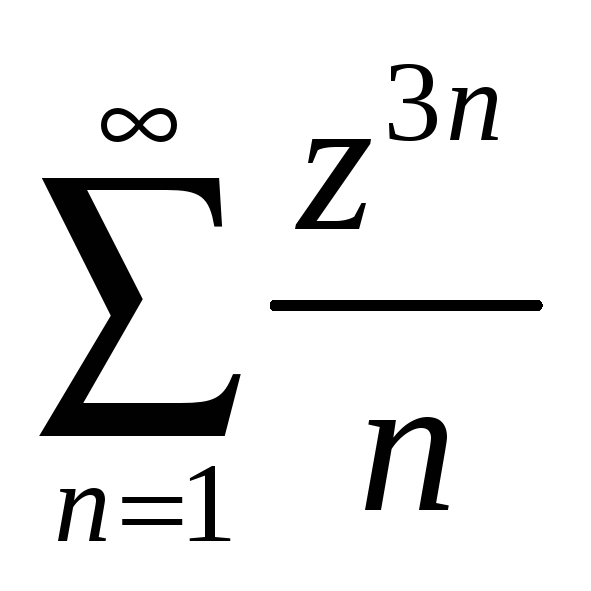
-
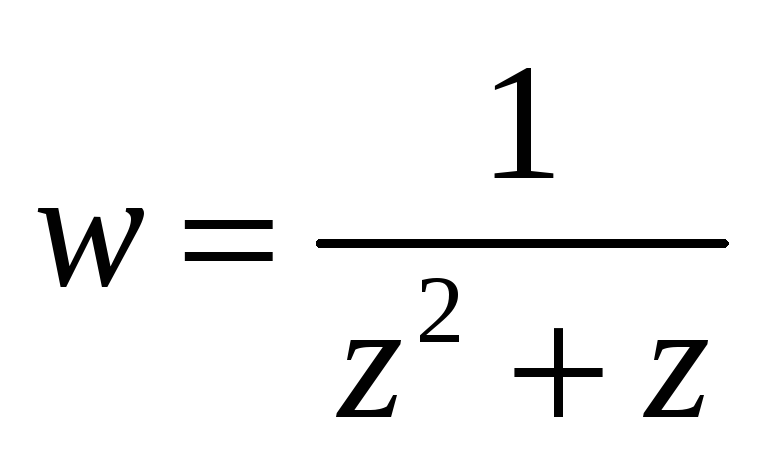 в
в
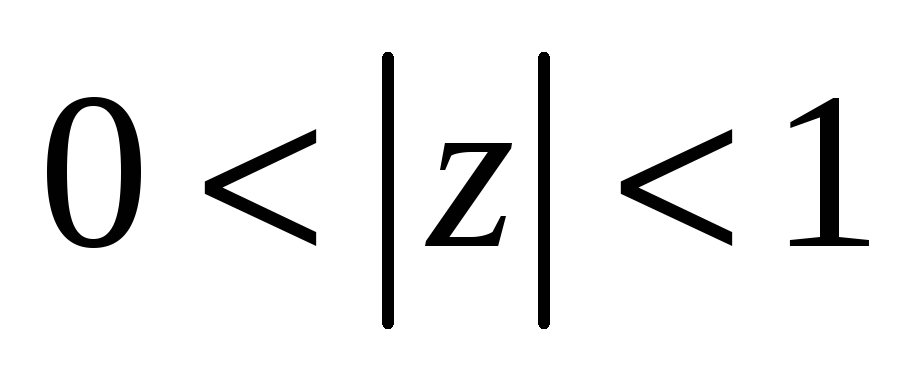
-

-

-
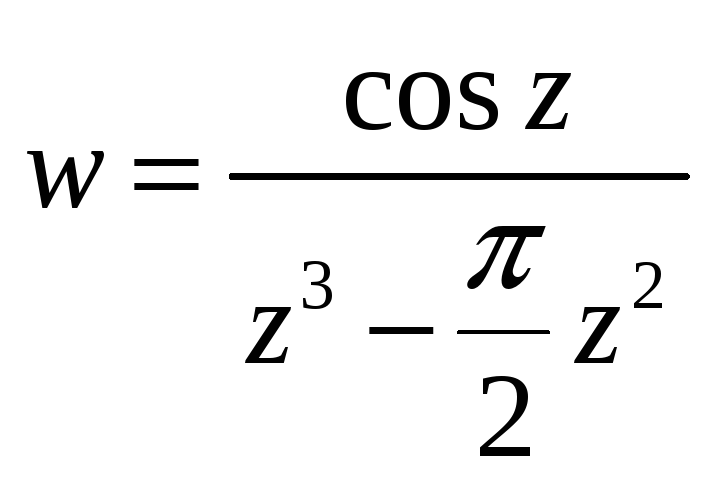
-
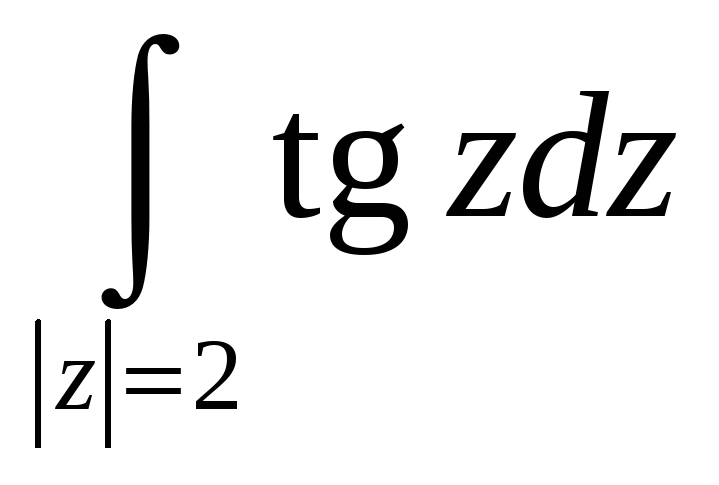
-

