Основы булевой алгебры

Для описания работы схем вычислительной техники и автоматики используют булеву алгебру.

Булевой функцией называют функцию f(x₁, x₂, х₃,…, x_n), аргументы которой x₁, x₁, x₂, …, x_n и сама функция принимают значение 0 или 1.

Таблицу, показывающую, какие значения принимает булева функция при всех сочетаниях значений её аргументов, называют таблицей истинности. Таблица истинности булевой функции n аргументов содержит 2ⁿ строк, n столбцов значений аргументов и 1 столбец значений функций. Например, таблицей 1 задана булева функция Y=f(x₁, х₂, х₃) от трех переменных х₁, x₂, х₃. Она содержит 2³ = 8 строк и четыре столбца.

Таблица №1

X1	X2	X3	Y
0	0	1	1
1	1	0	0
1	0	0	0
0	0	1	1
0	1	1	1
1	1	1	1
1	0	0	0
0	0	1	1

Булеву функцию y=f(x₁, x₂), определенную таблицей истинности 2, называют логическим сложением или дизъюнкцией и обозначают символом, т. е. используют такую запись: у=x₁x₂. На основании таблицы 2 можно записать таблицу 3 логического сложения. Она отличается от обычного сложения только тем, что 1+1 принимают равным 1.

Булеву функцию y=f(x₁,х₂), определенную таблицей истинности 4, называют логическим умножением или конъюнкцией и обозначают символом, т. е. используют запись у=х₁х₂. На основании таблицы истинности 4 можно записать таблицу 5 логического умножения. Она полностью совпадает с таблицей умножения для чисел 0, 1.

Логическое сложение обозначают также знаком «+», а логическое умножение–знаком «∙».

Булеву функцию у=f(x), определенную таблицей 6, называют отрицанием и обозначают её чертой, т. е. записывают у=.

Таблица №2 Таблица №3 Таблица №4 Таблица №5 Таблица №6

x1	x2	y	00=0 01=1 10=1 11=1	x1	x2	y	00=0 01=0 10=0 11=1	x
0	0	0		0	0	0		0	1
0	1	1		0	1	0		1	0
1	0	1		1	0	0
1	1	1		1	1	1

На основании таблиц логического сложения, умножения и отрицания можно записать:

а) 1+ x = 1, в) x + =1, д) , ж) ,

б) 0 + x = x, г) x + = x, е) , З) .

Для конъюнкции, дизъюнкции и отрицания справедливы следующие законы:

1) переместительный:

x₁+ x₂ = x₂ + x₁

2) сочетательный:

,

( x₁+ x₂) + x₃ = x₁+ (x₂ + x₃).

3) первый распределительный закон:

;

второй распределительный:

;

4) инверсный:

,

.

Любой из законов легко проверить путём составления таблиц истинности для обеих частей равенства. Например, проверим правильность закона . Составим таблицы №7 и №8.

Таблица №7 Таблица №8

x1	x2					x1	x2
0	0	0	1			0	0	1	1	1
0	1	0	1			0	1	1	0	1
1	0	0	1			1	0	0	1	1
1	1	1	0			1	1	0	0	0

Сравнивая столбцы значений функций для левой и правой частей равенства, видим, что эти значения совпадают, а следовательно, левая и правая часть равенства равна правой.

Структурная формула

Булево выражение y=f(x₁, х₂, ...,x_n) можно рассмотреть как структурную формулу, определяющую структуру логического устройства, цепь которого состоит из элементов И, ИЛИ, НЕ.

Обычно булева функция задается таблицей истинности, структурная формула которой записывается либо в так называемой совершенной дизъюнктивной нормальной форме (СДНФ), либо совершенной конъюнктивной нормальной форме (СКНФ).

СДНФ представляет собой логическую сумму (дизъюнкцию) нескольких логических произведений (конъюнкций), каждое из которых содержит все переменные или их отрицания. СДНФ булевой функции записывается на основании таблицы истинности следующим образом:

1. Число конъюнкций равно числу строк таблицы истинности, в которых функция равна 1 ( y=1).

2. Знак инверсии ставится над переменными, которые в соответствующих строках равны 0.

Например, для таблицы 1 СДНФ булевой функции будет содержать четыре конъюнкции, соединенные между собой логическим сложением:

Таблица №1

x3	x2	x1	y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

СКНФ представляет собой конъюнкцию нескольких дизъюнкций, каждая из которых содержит все переменные или их отрицания. СКНФ булевой функции на основании таблицы истинности записывается следующим образом:

1. Число дизъюнкций равно числу строк таблицы истинности, в которых функция равна 0 (у == 0).

2. Над теми переменными, которые в соответствующих строках равны 1, ставят знак инверсии.

Например, для таблицы 1 СКНФ булевой функции будет содержать четыре дизъюнкции соединенные между собой логическим умножением:

y =()()()()

Структурные формулы могут быть упрощены по законам алгебры логики. Такими преобразованиями пользуются для упрощения (минимизации) числа логических операций. Например, упростим структурную формулу:

y=

=

=

==.

Построение комбинационных схем по структурной формуле на однотипных базовых элементах

Рассмотрим логическую функцию , используя инверсный закон получим . Полученное выражение представляет собой логическую функцию элемента ИЛИ–НЕ на входы которого поданы переменные и . Переменную можно представить, как тогда исходную функцию можно записать . То есть заданная функцию можно собрать на двух логических элементах ИЛИ–НЕ рис. 1.

Рис. 1

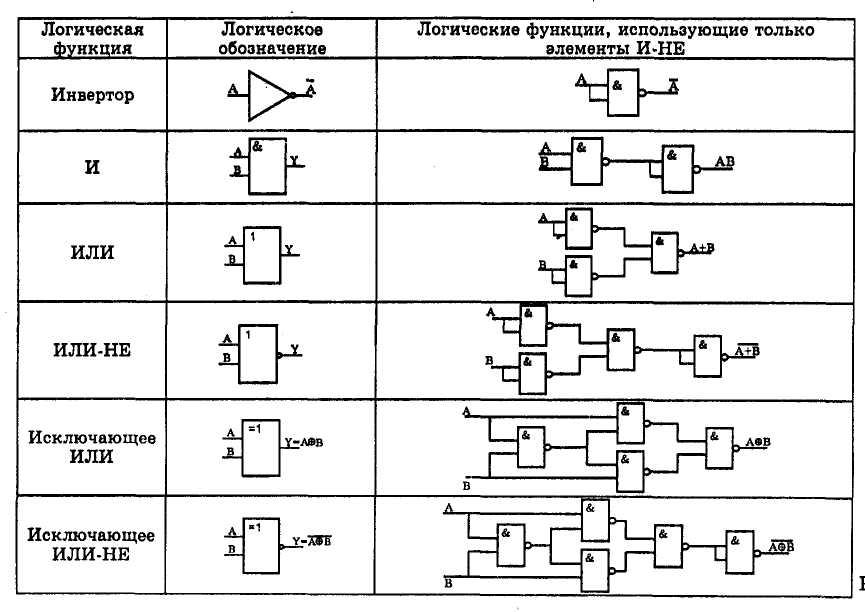
Элементы И-НЕ часто используются в качестве элементов других типов. На рисунке 2 показано как элементы И-НЕ могут быть использованы для создания других функций.

Рисунок 2