
- •Лабораторная работа № 1 группы и их подгруппы Вопросы для самоконтроля
- •Задачи к лабораторной работе
- •Задачи к лабораторной работе
- •Лабораторная работа № 3 линейные группы Вопросы для самоконтроля
- •Задание к лабораторной работе
- •Лабораторная работа № 5 порядок элемента Вопросы для самоконтроля
- •Задачи к лабораторной работе
- •Лабораторная работа № 6
- •Полупрямые и прямые
- •Произведения
- •Вопросы для самоконтроля
- •Задачи к лабораторной работе
- •Лабораторная работа № 7 группы, порожденные двумя элементами
Лабораторная работа № 7 группы, порожденные двумя элементами
Если группа
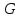 содержит элементы
содержит элементы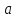 и
и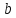 ,
то, очевидно, она содержит и циклические
подгруппы
,
то, очевидно, она содержит и циклические
подгруппы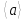 и
и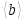 .
Что касается других подгрупп, содержащих
элементы
.
Что касается других подгрупп, содержащих
элементы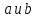 ,
то их принадлежность группе
,
то их принадлежность группе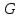 зависит от соотношений между элементами
зависит от соотношений между элементами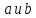 .
Наименьшая из подгрупп, содержащих
.
Наименьшая из подгрупп, содержащих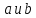 ,
называется подгруппой порождённой
элементами
,
называется подгруппой порождённой
элементами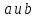 и обозначается как
и обозначается как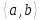 .
Простейшее соотношение междуa
и b
есть равенство
.
Простейшее соотношение междуa
и b
есть равенство
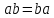 .
Например, если
.
Например, если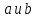 - перестановки, являющиеся независимыми
циклами, то
- перестановки, являющиеся независимыми
циклами, то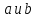 перестановочны в группе.
перестановочны в группе.
Другим соотношением
между
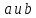 может быть равенство
может быть равенство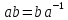 .
.
1.
Пусть
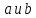 - элементы конечной группы и
- элементы конечной группы и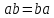 .
.
1.1.
Докажите, что
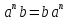 для всех
для всех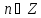 .
.
1.2. Пусть, кроме того,
элемент
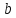 имеет порядок 2. Заполните таблицу
умножения.
имеет порядок 2. Заполните таблицу
умножения.
1.3. Докажите, что множество
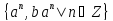 образует подгруппу
образует подгруппу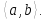
2. Пусть
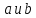 - элементы конечной группы и
- элементы конечной группы и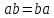 .
.
2.1. Докажите что
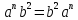 .
.
2.2. Пусть, кроме того,
элемент
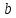 имеет порядок 3. Заполните таблицу
умножения
имеет порядок 3. Заполните таблицу
умножения
2.3. Докажите, что множество
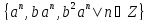 образует подгруппу
образует подгруппу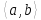 .
.
3. Пусть
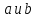 - элементы группы и
- элементы группы и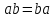 .
.
3.1. Докажите что
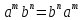 для любых натуральных
для любых натуральных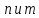 .
.
3.2. Докажите, что множество
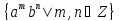 образует подгруппу
образует подгруппу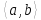 .
.
4.Пусть
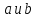 - элементы группы и
- элементы группы и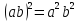 .
Докажите что
.
Докажите что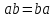 .
.
5. Пусть
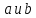 - элементы группы и
- элементы группы и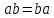 .
Докажите что
.
Докажите что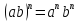 для всех целых
для всех целых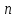 .
.
6. Если
 то каков порядок перестановки
то каков порядок перестановки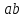 ?
?
7. Если
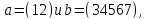 то каков порядок перестановки
то каков порядок перестановки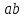 ?
?
8. Если
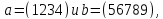 то каков порядок перестановки
то каков порядок перестановки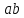 ?
?
9. Если перестановки
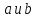 являются циклами длины
являются циклами длины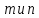 соответственно, и наибольший общий
делитель для
соответственно, и наибольший общий
делитель для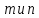 есть
есть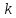 ,
то каков порядок перестановки
,
то каков порядок перестановки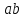 ?
?
10. Приведите пример,
показывающий, что если
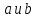 - элементы группы,
- элементы группы,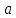 имеет порядок 6,
имеет порядок 6,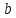 имеет порядок 10, то произведение
имеет порядок 10, то произведение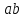 может иметь порядок, отличный от 30. Даже
когда
может иметь порядок, отличный от 30. Даже
когда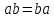 .
.
11. Пусть
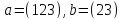
11.1. Проверьте, что
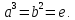
11.2. Проверьте, что

11.3. Вычислите перестановки
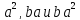 .
.
11.4. Проверьте, что
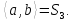
12. Пусть
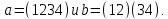
12.1. Проверьте, что
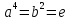 .
.
12.2. Проверьте, что
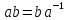 .
.
12.3. Вычислите перестановки
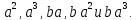
12.4. Проверьте, что
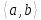 - группа симметрий квадрата.
- группа симметрий квадрата.
13. Пусть
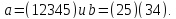
13.1. Проверьте, что
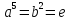 .
.
13.2. Проверьте, что
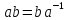 .
.
13.3. Вычислите перестановки
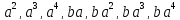 .
.
13.4. Проверьте, что для правильного пятиугольника с вершинами 1, 2, 3, 4 и 5 число симметрий описывается данными перестановками.
14. Пусть
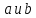 - элементы группы,
- элементы группы,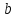 имеет порядок 2 и
имеет порядок 2 и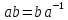 .
.
14.1. Рассмотрите произведение
 c двух точек зрения: с точки зрения, что
c двух точек зрения: с точки зрения, что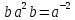 ,
и с другой точки зрения, что
,
и с другой точки зрения, что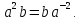
14.2. Расширьте этот метод
для доказательства того, что
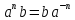 для всех целых n.
для всех целых n.
14.3. Заполните соответствующую таблицу умножения
14.4. Докажите, что множество
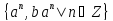 образует подгруппу
образует подгруппу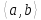 .
.
15. Пусть группа G порождается элементом a порядка n и элементом b
порядка 2, которые связаны
соотношением
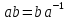 .
.
15.1. Докажите, что
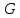 состоит из
состоит из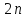 элементов.
элементов.
15.2. Докажите, что каждый
элемент вида
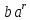 имеет порядок 2.
имеет порядок 2.
16. Представьте каждый
элемент из
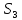 как произведение транспозиций.
как произведение транспозиций.
Докажите, что
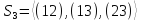 .
.
17. Докажите, что множество
всех транспозиций из
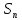 порождает группу
порождает группу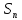 .
.
18. Вычислите произведение
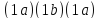 и установите, что множество транспозиций
и установите, что множество транспозиций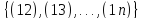 порождает группу
порождает группу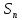 .
.
19. Вычислите произведения
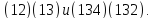
20. Докажите, что каждая чётная перестановка может быть записана в виде произведения циклов длины 3.
21. Докажите, что все циклы
длины 3 порождают
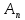 .
.
