
логика
.pdf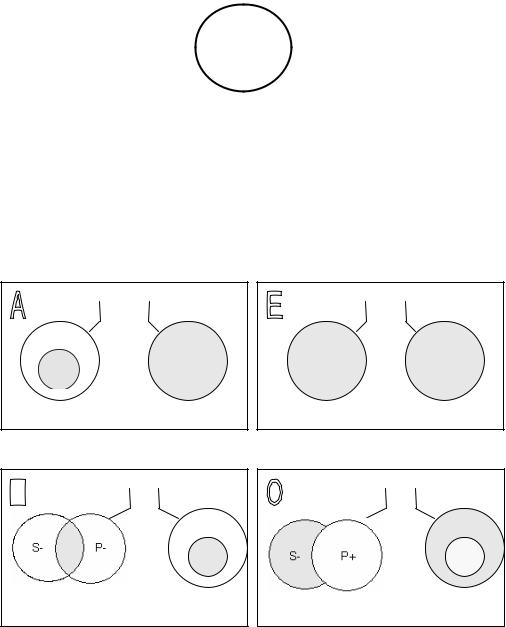
Классификация простых суждений
|
|
|
|
|
|
По объёму субъекта |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Единичные, общие, |
|
|
|
|
|
|
|
|||||
|
По содержанию пре- |
|
|
|
|
частные |
|
По типу логических |
|
|||||||||
|
|
|
диката |
|
|
|
|
|
|
|
|
|
|
|
союзов |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Существования, |
|
|
|
|
|
|
|
|
|
Соединительные, |
|
|||||
|
|
атрибутивные, |
|
|
|
S есть P |
|
|
разделительные, |
|
||||||||
|
|
|
отношения |
|
|
|
|
|
|
условные |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
По количеству |
|
|
|
|
По модальности |
|
|
|
|||||||
|
|
|
связки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объектной |
|
|
|
|
|
Логической |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Утвердительные, отри- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Действительности, |
|
|
Проблематические, |
|
||||||||||
|
|
цательные, отрицаю- |
|
|
|
|
|
|||||||||||
|
|
|
возможности, необхо- |
|
|
|
достоверные |
|
||||||||||
|
|
|
щие |
|
|
|
|
|
||||||||||
|
|
|
|
|
димости |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема 13. Классификация простых суждений
Объединённая классификация простых суждений Общеутвердительные Общеотрицательные
Все S есть P |
Ни одно S не есть P |
|||
P- |
|
|
|
|
S+ |
P+ S+ |
S+ |
P+ |
|
|
|
|
||
S подчинён P |
S и P равнозначны |
объём S и объём P полностью ис- |
||
ключают друг друга |
||||
|
|
|||
Чатноутвердительные
Некоторые S есть P
S-
P+
S и P перекрещивающиеся понятия или P
починяется S
Чатноотрицательные
Некоторые S не есть P
S-
P+
часть объёма S несовместима с объёмом P
Схема 14. Объединённая классификация простых суждений
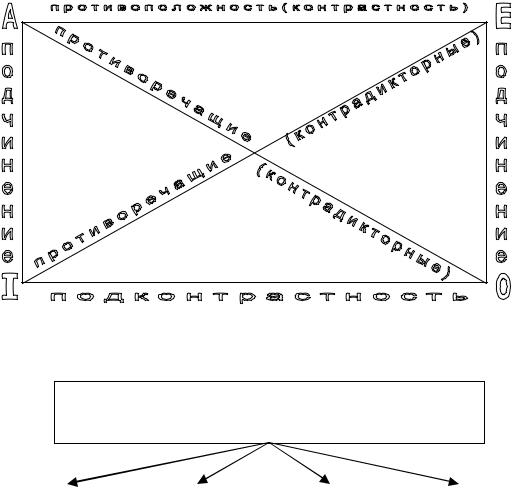
Отношения между простыми суждениями (рассматривается с помощью логического квадрата)
Эти отношения устанавливаются не между любыми, а лишь между сравнимыми, т. е. имеющими общий смысл, суждениями.
Схема 15. Отношения между простыми суждениями
Сложные суждения – это суждения, в которых можно выделить простые части, являющиеся в свою очередь суждениями (или суждения, состоящие из нескольких простых суждений).
Соединительные |
|
Разделительные |
|
Условные |
|
Эквивалентные |
(конъюнктивные) |
|
(дизъюнктивные) |
|
(импликативные) |
|
|
|
|
|
|
|
|
|
Это суждения, обра- |
Это суждения, обра- |
Это суждения, обра- |
||||
зованные |
посредст- |
зованные |
посредст- |
зованные |
посредст- |
|
вом связи двух или |
вом связи двух или |
вом связи двух |
или |
|||
более простых суж- |
более простых суж- |
более простых |
суж- |
|||
дений |
логическим |
дений |
логическим |
дений |
логическим |
|
союзом «и», а также |
союзом «или». |
союзом «если... то...». |
||||
другими |
аналогич- |
Формула дизъюнкти- |
Формула |
данного |
||
ными союзами. |
вного |
суждения: |
суждения: «АÆВ». |
|||
Структура конъюнк- |
«АvВ». |
|
|
|
|
|
тивного |
суждения: |
|
|
|
|
|
«А^В». |
|
|
|
|
|
|
Схема 16. Сложные суждения
Это суждения, образованные посредством связи двух или более простых суждений логическим союзом «тогда и только тогда когда» Формула данного
суждения: «А≡В».
Логические операции с суждениями
|
Преобразование суждений |
|
|
|
Отрицание суждений |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Преобразование про- |
|
Преобразование |
|
Отрицание простых |
|
Отрицание сложных |
||||
стых суждений |
|
сложных суждений |
|
суждений |
|
суждений |
||||
|
|
|
|
|
|
|
|
|
|
|
Обращения Конъюнкция
Превращения Дизъюнкция
Противопоставления Импликация
Схема 17. Логические операции с суждениями
Обращение – это преобразование суждения путём перестановки его субъекта и предикаты местами.
Закономерности обращения
Общеутвердительные |
|
Частноутвердительные |
|
Общеутвердительные |
суждения преобразуются |
|
суждения преобразуются |
|
суждения преобразуются в |
в частноутвердительные |
|
в частноутвердительные |
|
общеутвердительные |
|
|
|
|
|
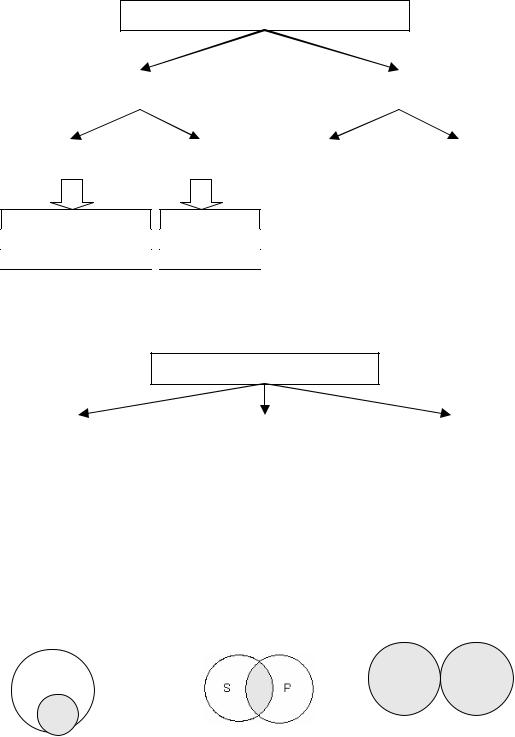
Формула обращения «Все S есть P» – «некоторые S есть P». Так, в суждении «Все адвокаты юристы» поставим субъект на место предиката, а предикат на место субъекта. В результате получим: «Некоторые юристы – адвокаты». Это графически можно представить так:
Формула обращения: «некоторые S есть P и некоторые P естьS».
Пример: «Некоторые юристы – депутаты Госдумы, некоторые депутаты Госдумы – юристы». Это можно графически представить так:
Формула: «ни одно S не есть P, ни одно P ни есть S». Например, «Ни один свидетель не явился в суд – ни один явившийся в суд не является свидетелем».
Графически можно представить так:
P |
|
S |
P |
S |
|
где S – явившиеся, |
|
|
где S – депутаты, |
|
|
где S – адвокаты, |
P – свидетели |
|
P – юристы |
P – юристы |
|
|
|
Схема 18. Обращение и его закономерности |
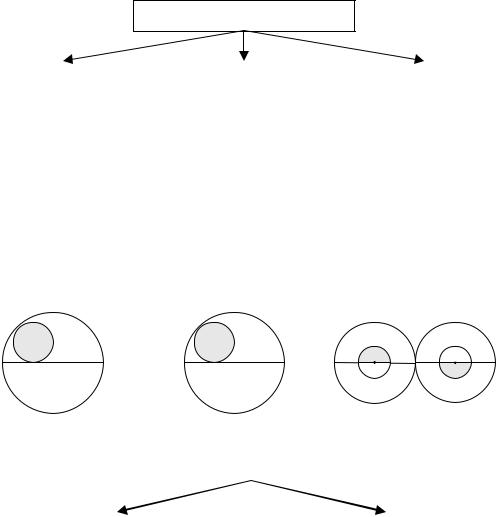
Превращение – это преобразование суждения путём перемены его качества на противоположное.
Закономерности превращения
Общеутвердительные |
|
Общеотрицательные |
|
Частноутвердительные |
|
|||||||||||
суждения преобразуются |
|
суждения преобразуются |
|
сужденияпреобразуются в |
|
|||||||||||
в общеотрицательные |
|
в общеутвердительные |
|
частноотрицательныеи |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
наоборот |
|
|
|
|
Формула: «Ни одно S не Формула: «Ни |
|
одно S не |
|
Формула: «Некоторые S не |
||||||||||||
есть P». Так суждение «Все |
есть не Р, все |
S есть Р». есть P – некоторые S не |
||||||||||||||
адвокаты – юристы» по ка- |
Пример: «Ни одно преступ- |
|
есть не – P». Пример: «Не- |
|||||||||||||
честву |
утвердительное. |
ление не осталось нерас- |
|
которые свидетели дали не- |
||||||||||||
Превращаем его в отрица- |
крытым – все преступления |
|
верные показания – некото- |
|||||||||||||
тельное так, чтобы при |
раскрыты». |
Графическое |
|
рые свидетели не дали не- |
||||||||||||
этом, его смысл не измепредставление: |
|
|
|
|
верных показаний». |
|
|
|
||||||||
нился: «Ни один адвокат не |
|
|
|
|
|
|
Графическое |
представле- |
||||||||
является юристом». Графи- |
|
|
|
|
|
|
ние: |
|
|
|
|
|
|
|||
ческое представление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S |
|
|
|
S |
|
|
|
|
P |
S |
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
не – Р |
не Р |
|
|
|
|
не |
|
–Р |
не |
–Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Схема 19. Превращение и его закономерности |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Противопоставление |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
Противопоставление субъекту |
|
|
|
Противопоставление предикату |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Так называется преобразование суждения |
|
|
Это преобразование суждения путём пре- |
|||||||||||||
путём обращения и последующего пре- |
|
|
образования и последующего обращения. |
|||||||||||||
вращения. Пример: «Все адвокаты – юри- |
|
|
Пример: суждение «Все адвокаты – юри- |
|||||||||||||
сты» обратим в суждение «Некоторые |
|
|
сты» сначала превратим в суждение «Ни |
|||||||||||||
юристы – адвокаты», а последнее в свою |
|
|
один адвокат не является не юристом», а |
|||||||||||||
очередь превратим в суждение «Некоторые |
|
|
последнее обратим в суждение «Ни один |
|||||||||||||
юристы не есть не адвокаты», то получим |
|
|
юрист не является адвокатом». Получает- |
|||||||||||||
противопоставление субъекту. Предикат |
|
|
ся, что предикату |
исходного |
суждения |
|||||||||||
заключительного суждения – «не адвока- |
|
|
«юристы» мы противопоставили понятие |
|||||||||||||
ты» противопоставляется субъекту исход- |
|
|
«не юристы» и сделали его субъектом но- |
|||||||||||||
ного суждения – «адвокаты». |
|
|
|
|
вого суждения. |
|
|
|
|
|
|
|||||
Схема 20. Противопоставление
Отрицание суждения
Если формула простого атрибутивного утвердительного суждения – «S есть P», то формула его отрицания будет: «Неверно, что S есть P» или «S не есть P». Например, «Все судьи справедливы». «Неверно, что все судьи справедливы» или «Не все судьи справедливы». Отрицанию могут подвергаться и отрицательные суждения. Если формула отрицательного суждения – «S не есть P», то его отрицание будет выражено формулой: «Неверно, что S не есть P».
Сущность этой логической операции составляет замена одного исходного суждения другим, не только не совместимым с ним, но и противоречащим ему. Языковыми средствами выражения такой операции служат обороты речи типа «неверно что...» или частица «не» и ей подобные.
Схема 21. Отрицание суждения
5. Умозаключение
Умозаключение – это форма мышления, посредством которой из одного или нескольких суждений с необходимостью выводится новое суждение.
Структура умозаключения
Посылки |
|
Заключения |
|
Связь между посылками |
|
|
и выводом |
||
|
|
|
|
|
|
|
|
|
|
Это исходное, и притом из- |
Это производное, и притом |
|
вестное знание, служащее |
новое знание, полученное |
|
основанием |
умозаключе- |
из посылок и выступающее |
ния. |
|
их следствием. |
Это отношение между ними, делающее возможным переход от одного к другому, – отношение логического следования
Схема 22. Умозаключение и его структура
Пример:
Все художники тонко чувствуют природу (Посылка). Левитан – художник (Посылка).
Следовательно, Левитан тонко чувствует природу (Заключение).
Основные виды умозаключения
Дедуктивные |
|
Индуктивные |
|
Традуктивные |
|
|
(по аналогии) |
||
|
|
|
|
|
|
|
|
|
|
Заключение идёт от знания |
|
Заключение идёт от знания |
|
Заключение идёт путём пе- |
большей степени общности |
|
меньшей степени общности |
|
реноса свойств одного |
к знанию меньшей степени |
|
к знанию большей степени |
|
предмета на другой предмет |
общности (признак, прису- |
|
общности (признак, прису- |
|
при сходстве их в сущест- |
щий классу предметов при- |
|
щий нескольким представи- |
|
венных признаках. |
надлежит и каждому пред- |
|
телям класса предметов, ве- |
|
|
ставителю этого класса). |
|
роятно, принадлежит и все- |
|
|
|
|
му классу предметов). |
|
|
Схема 23. Основные виды умозаключения
Дедуктивное умозаключение – это такое умозаключение, в котором мыслительный процесс идёт от более общего значения к менее общему.
(Пример: Все люди смертны. Сократ человек. Следовательно, Сократ смертен.)
Непосредственные умозаключения |
|
Опосредованные умозаключения |
|
|
|
Это такие умозаключения, которые дела- |
Это такие умозаключения, которые делают- |
|
ются из одной посылки. |
сяизнескольких(двухиболее) простых. |
|
Пример: Все поэты – впечатлительные |
Пример: Наиболее распространённой и |
|
люди. Следовательно, некоторые впечат- |
важной формой опосредованного умозак- |
|
лительные люди – поэты. |
лючения выступает простой категориче- |
|
|
|
ский силлогизм. |
Схема 24. Дедуктивное умозаключение
Простой категорический силлогизм
Это опосредованное дедуктивное умозаключение, состоящее из двух категорических суждений (посылок), особым образом связанных между собой, и заключения.
Пример: Все законы объективны, т. е. не зависят от людей. Конституция России– закон. Следовательно, КонституцияРоссиинезависитотлюдей.
Структура силлогизма
Две посылки |
|
Заключение |
|
Термины S, P, M |
|
|
|
|
|
Схема 25. Структура силлогизма
Пример: Все люди (M) смертны (P). (Большая посылка) Сократ (S) – человек (M). (Меньшая посылка) Следовательно, Сократ (S) смертен (P). (Заключение)
Меньшим термином называется субъект заключения. Он обозначается буквой S.
Большим термином называется предикат заключения (буква P). Средний термин входит в обе посылки, обеспечивая логическую
связь между ними (буква M).
Большаяпосылка– посылка, вкоторуювходитбольшийтермин(P).
Меньшаяпосылка– посылка, вкоторуювходитменьший термин (S).
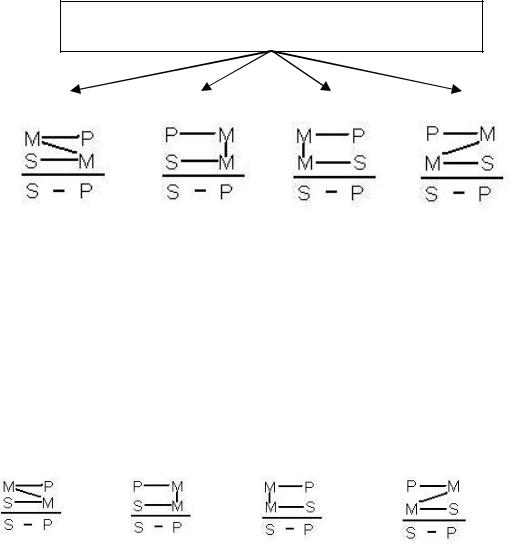
Фигуры силлогизма – это разновидности силлогизма, различающиеся положением среднего термина (М).
1-я фигура |
|
2-я фигура |
|
3-я фигура |
|
4-я фигура |
Пример: Всякое преступление (М) есть правонарушение (Р). Следовательно кража (S) есть правонарушение (P).
Пример: Все юристы Пример: Все учебниПример: Некоторые (Р) знают логику (М). ки (М) полезны (Р). пенсионеры (Р) – раИванов (S) не знает Все учебники – книги ботающие (M). Все логику (М). Значит, (S). Следовательно, работающие (M) поИванов (S) не юрист некоторые книги (S) лучают зарплату (S).
(P). полезны (P). Следовательно, некоторые получаю-
щие зарплату (S) –
Схема 26. Фигуры силлогизма
Модусы силлогизма – это разновидности каждой фигуры силлогизма, различающиеся количеством и качеством суждений, составляющих посылки.
1-я фигура |
2-я фигура |
3-я фигура |
4-я фигура |
A, E, J, O |
A, E, J, O |
A, E, J, O |
A, E, J, O |
A, E, J, O |
A, E, J, O |
A, E, J, O |
A, E, J, O |
Схема 27. Четыре фигуры силлогизма их модусы
Каждая из посылок может быть общеутвердительной (A), общеотрицательной (E), частноутвердительной (J), частноотрицательной (O). Поэтому в одной фигуре возможно 16 модусов (4 × 4). Так, если большая посылка – общеутвердительная (A), то могут быть модусы: AA, AE, AJ, АО. Если большая посылка – общеотрицательная (E), то могут быть модусы: EA, EE, EJ, EO. Если большая посылка – частноутвердительная (J), то могут быть модусы: JA, JE, JJ, JO. Если большая посылка – частноотрицательная (O), то могут быть модусы: OA, OE, OJ, OO. Таким образом, в четырёх фигурах соответственно будут 64 модуса (16 × 4).
Индуктивное умозаключение – это такое умозаключение, в котором ход мысли идёт от менее общего значения к более общему
Полная индукция |
|
Неполная индукция |
|
|
|
Называется такое умозаключение, в кото- |
Называется умозаключение обо всём |
|
ром общий вывод получается в результате |
классе предметов в целом на основе изу- |
|
изучения всех предметов данного класса. |
чения лишь части предметов данного |
|
Пример: |
класса. |
|
Понедельник – солнечный день; |
Пример: Ласточки перед дождём летают |
|
Вторник – солнечный день; |
низко над землёй. |
|
………… |
Всегда ласточки перед дождём летают |
|
День N – солнечный день; |
низко над землёй. |
|
Понедельник, вторник ……день N исчер- |
|
|
пывают все дни недели. Следовательно, |
|
|
неделя была солнечной. |
|
|
Схема 28. Индуктивное умозаключение

Традуктивное умозаключение – это вероятный вывод о сходстве изучаемого предмета в интересующем нас признаке с другим предметом на основе известного их сходства в ряде других существующих признаков.
Строгая аналогия (сильная) |
|
Нестрогая аналогия (слабая) |
|
|
|
Это умозаключение, в котором переносимый признак необходимым образом связан с другими, сходными признаками (будучи, например, их следствием или, наоборот, причиной). В этом случае вывод может стать достоверным.
Например, студент А часто строит выводы на основе поспешных обобщений и потому рассуждения его часто бывают ошибочными.
Зная, что студент Б также часто делает поспешные обобщения, можно заключить, что его рассуждения часто бывают ошибочными.
Это умозаключение, в котором переносимый признак непосредственно не связан со сходным, но может иметь место. Такая аналогия даёт вероятный вывод.
Например, железо обладает специфическим блеском, ковкостью теплопроводимостью, электропроводимостью. Неизвестное тело серо-стального цвета обладает теплопроводимостью. Это неизвестное тело принадлежит к группе металлов и значит, обладает ковкостью и электропроводимостью.
Схема 29. Традуктивное умозаключение
6. Законы логики
Рис. 7. Законы логики

Рис. 8. Законы тождества
Рис. 9. Закон противоречия
