учебное пособие / лекція 6

ЛЕКЦІЯ

ТРИГОНОМЕТРИЧНІ ВИРАЗИ ТА ЇХ ПЕРЕТВОРЕННЯ

6.1. Відношення сторін в трикутнику

Розглянемо спочатку прямокутний трикутник АВС.

Позначимо сторони прямокутного трикутника через а, b, с, де с — гіпотенуза (рис. 1), — прямий.

Рис. 1

В такому трикутнику вводять наступні співвідношення

,

. (1)

Нехай АВС — довільний трикутник зі сторонами а, b, с і кутами (рис. 2).

Рис. 2

Через позначимо радіус описаного кола.

Справджується формула

, (2)

яку називають теоремою синусів.

Доведення формул (2) випливає з того, що всі вписані в коло кути, які спираються на одну хорду, рівні між собою (рис. 3).

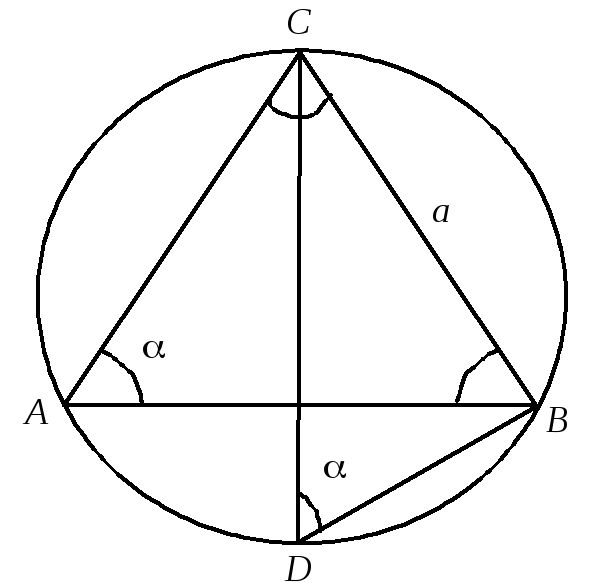
Рис. 3

Проведемо діаметр . Кут . Кут — прямий, а тому . Аналогічно доводяться рівності , , з яких випливає формула (2).

При розв’язуванні трикутників часто використовують теорему косинусів, яка приводить до формул:

,

,

. (3)

Доведемо першу формулу (рис. 4).

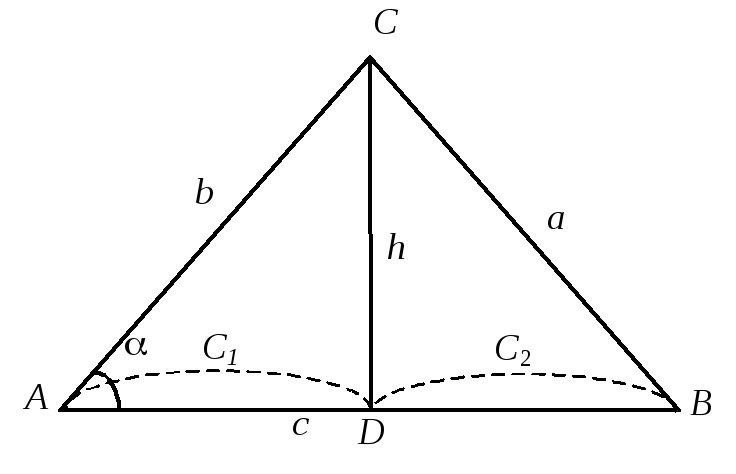
Рис. 4

З трикутника знаходимо:

, , , .

Скориставшись теоремою Піфагора, дістаємо першу з формул (3):

.

Прямий кут поділяється на 90 рівних між собою частин, — градусів. Кут 30 становить одну третину а, кут 45 — половину прямого кута. Наведемо таблицю значень функцій , .

	0	30	45	60	90
	1				0

6.2. Означення і графіки тригонометричних функцій

Дано прямокутну систему координат . Нехай — одиничний вектор, що утворює довільний кут з віссю (рис. 1). Точка А міститься на колі одиничного радіуса з центром у початку координат О.

Рис. 1

Кут вимірюється довжиною дуги , яка називається радіанною мірою кута . Оскільки радіус окружності дорівнює одиниці, то довжина всього кола . Прямий кут вимірюється довжиною однієї четвертої частини кола, що дорівнює . Наведемо таблицю відповідності кутів у радіанній і градусній мірі.

0
0	30	45	60	90	180	270	360

Функція — парна, — непарна, тобто , .

Осі координат розбивають координатну площину на чотири частини, які називаються чвертями. Говорять, що кут належить першій чверті, якщо ; кут належить другій чверті, якщо ; кут належать третій чверті, якщо ; кут належить четвертій чверті, якщо (рис. 2).

Рис. 2

Якщо кут виходить за межі відрізка , то знаходимо ціле число таке, що . Кут належить тій четвер­ті, якій належить кут .

Знаки тригонометричних функцій у різних четвертях ілюструє рис. 3.

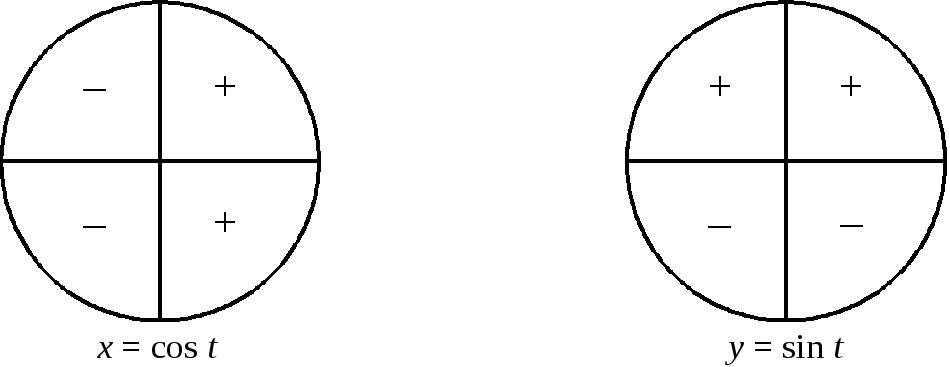
Рис. 3

Визначимо основні тригонометричні функції:

, .

Функцією x = cos t називається проекція на вісь одиничного вектора , що утворює кут з віссю .

Функцією y = sin t називається проекція на вісь одиничного вектора , що утворює кут з віссю .

З теореми Піфагора випливає рівність

або

. (1)

Ця рівність дає змогу найти значення функції , коли відоме значення функції :

.

Аналогічно можна знайти значення функції , коли відоме значення функції :

.

Вибір знака залежить від того, в якій чверті лежить кут .

Наведемо деякі властивості функцій , .

1. Область визначення — усі значення .

2. Область значень — відрізок , оскільки .

3. Функції , періодичні з періодом , оскільки

, .

Приклад. Дано: , . Знайти .

• Оскільки в другій четверті 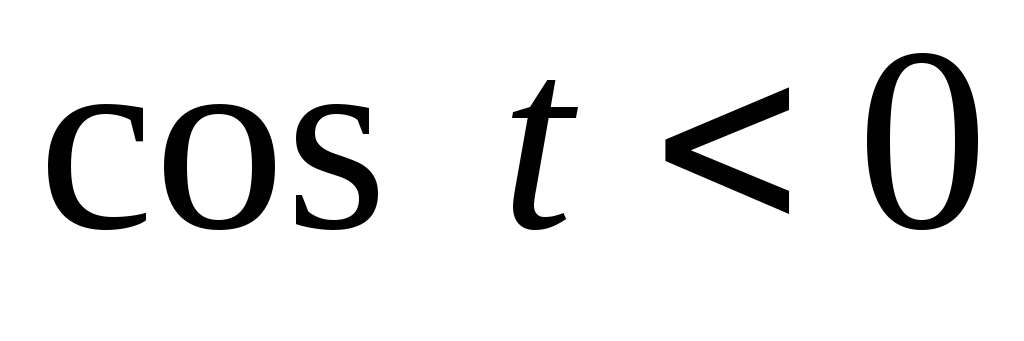, то

.

Приклад. Дано: , . Знайти .

• Оскільки в третій четверті 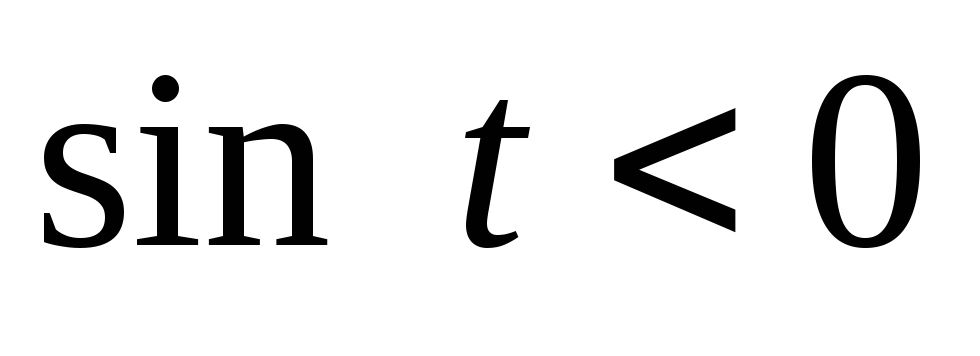, то

.

Побудуємо графіки функцій , (рис. 4).

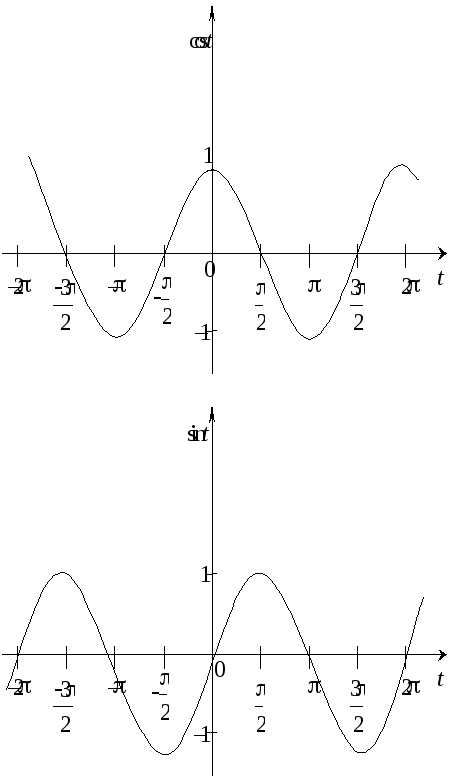
Рис. 4

З графіків бачимо, що виконуються такі властивості:

, , (2)

, , (3)

, . (4)

З формул (2)—(4) випливають такі формули:

(5)

Функції tg t, ctg t визначаються за формулами:

, . (6)

1. Область визначення функції : , , функції : , .

2. Область значень: , .

3. Функції , мають період .

4. Функції , непарні відносно .

З формул (2) — (5) випливають такі рівності

,

, (7)

.

Функції , можна визначити графічно. Проводимо дотичну до одиничного кола у точці (1, 0), яка називається лінією тангенсів. Нехай вектор утворює кут з віссю (рис. 5). Продовжимо вектор до перетину з лінією тангенсів у точці С. Для ординати точки перетину С маємо: .

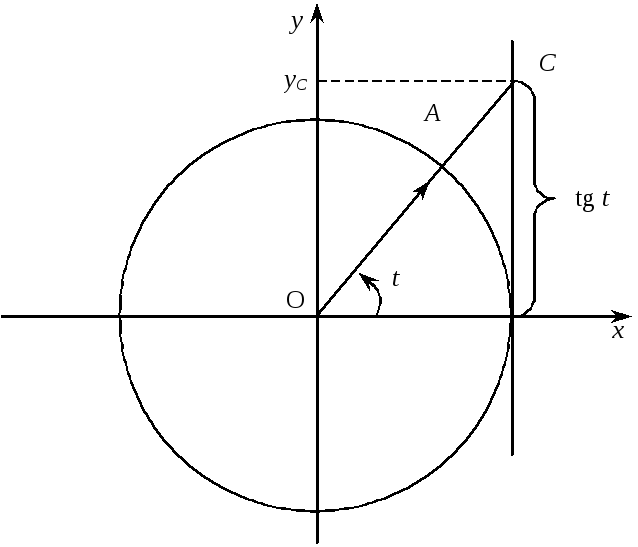
Рис. 5

Аналогічно проводимо дотичну до одиничного кола в точці (0, 1). Ця дотична називається лінією котангенсів. Продовжимо вектор до перетину з лінією котангенсів в точці (рис. 6).

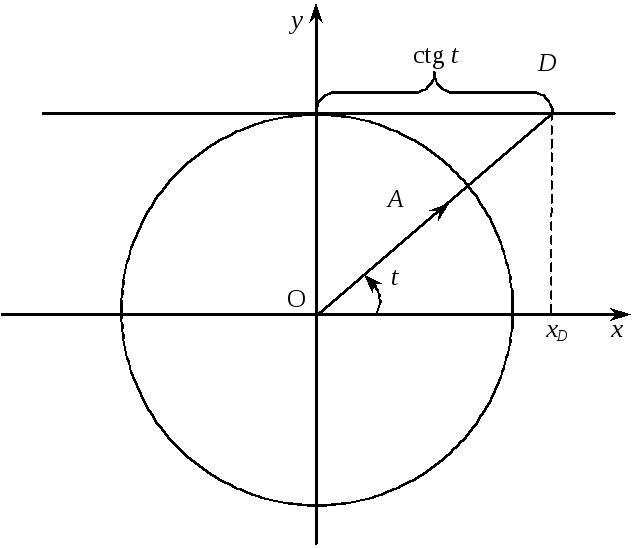
Рис. 6

Для абсциси точки перетину маємо: .

Побудуємо графіки функцій .

Функція зростає на кожному проміжку , (рис. 7).

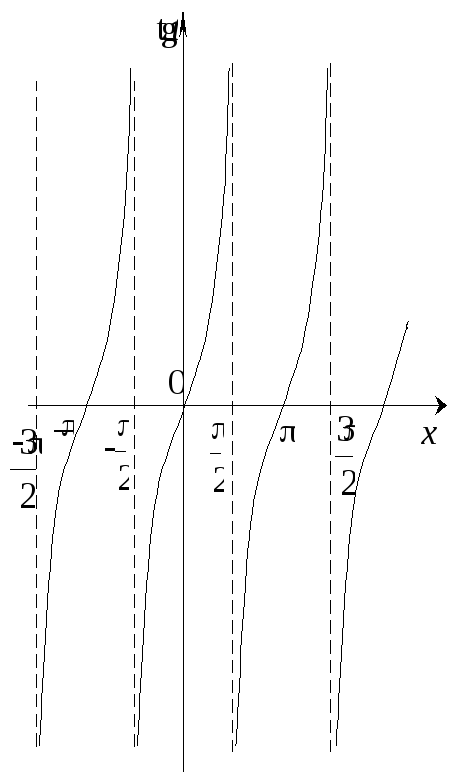
Рис. 7

Функція спадає на кожному проміжку , (рис. 8).

Для функцій , у точках розриву виконуються гранич­ні співвідношення:

; ;

; ;

; ;

; 0.

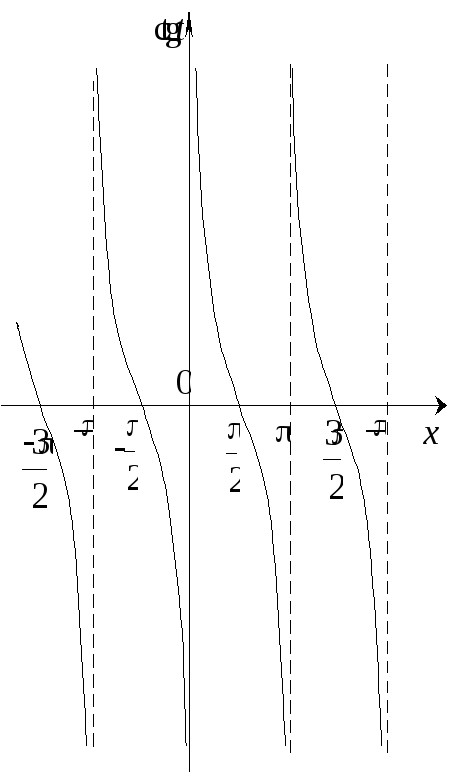
Рис. 8

Функція має точки розриву , . Функція має точки розриву , .

6.3. Основні тригонометричні тотожності

З формул (1)—(6) підрозд. 6.2 випливають такі рівності

;

; ; ;

, .

Ці рівності дають змогу знаходити значення тригонометричних функцій , коли відомі значення однієї з них.

Нехай, наприклад, кут міститься в першій четверті, . З рівності знаходимо: ; ; ; ; .

6.4. Формули додавання кутів

Нехай точки А, В містяться на одиничному колі і вектори , утворюють кути , з віссю (див. рисунок).

Знаходимо відстань :

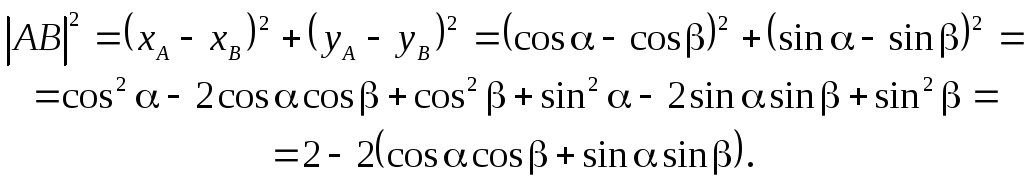
З теореми косинусів для трикутника ОАВ знаходимо

Порівнюючи результати, дістаємо формулу:

. (1)

Замінивши знак кута у формулі (1) на протилежний, дістанемо:

. (2)

Замінимо у формулі (1) кут на кут :

.

Здобута рівність за допомогою формул (5) підрозд. 6.2 набирає вигляду:

. (3)

Замінивши у формулі (3) кут на , дістанемо:

. (4)

При маємо формули подвійного кута

(5)

Додаючи до останньої формули (5) та віднімаючи від неї тотожність , дістаємо формули:

(6)

які можна записати у вигляді:

. (7)

Знайдемо, наприклад, вирази для , :

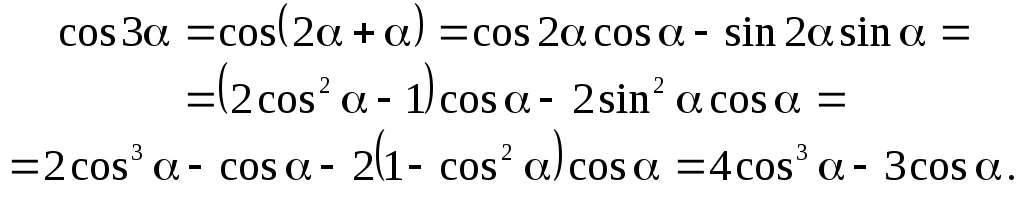
Аналогічно дістаємо:

Замінивши на у формулах (7), дістанемо:

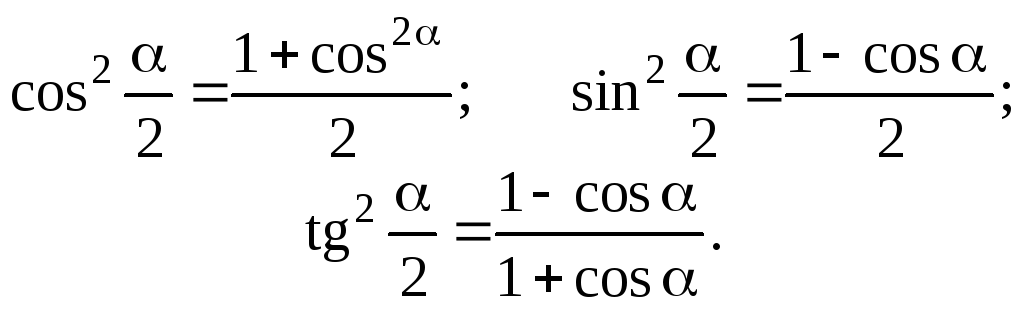(8)

Для функції маємо:

.

Поділивши чисельник і знаменник на добуток , дістанемо формулу додавання кутів:

. (9)

Замінивши на , отримаємо формулу

. (10)

6.5. Формули зведення

Часто доводиться перетворити вирази

на тригонометричні функції від , використовуючи формули зведення.

Наприклад, оскільки , , маємо:

(1)

Аналогічно виводяться формули:

. (2)

Наведемо формули, які потрібно запам’ятати:

(3)

Найчастіше застосовувані формули зведення вміщено в таблиці.