16.1. Означення та основні властивості векторів

Відрізок, на якому задано напрям, тобто зазначено початок і кінець, називається вектором. Вектори позначаються ,або,і т. ін. (рис. 1). Модуль вектора— довжина відрізкаАВ; — позначення. Якщо початок вектора збігається з його кінцем, то такий вектор називаєтьсянульовим.

Вектори, що належать паралельним прямим або одній і тій самій прямій, називаються колінеарними (наприклад, вектори ,,на рис. 1).

Рис. 1

Два вектори називаються однаково напрямленими, якщо вони колінеарні і їхні кінці містяться в одній півплощині відносно прямої, що сполучає їхні початки (вектори ,, на рис. 1).

Два вектори називаються рівними, якщо вони однаково напрямлені і їхні модулі рівні.

Колінеарні вектори і, зображені на рис. 1, називаютьсяпротилежно напрямленими.

Множення вектора на число. Вектором називається вектор, колінеарний векторуі однаково з ним напрямлений, якщоk > 0, та протилежно напрямлений, якщо k < 0, і такий, що

.

На рис. 1 зображено вектори і.

Теорема 1. Два ненульових вектори іколінеарні тоді і тільки тоді, коли існує таке числоk, що

Теорема 2. Від будь-якої точки можна відкласти вектор, що дорівнює даному.

Сумою двох векторів іназивається вектор(правило трикутника; рис. 2). Вектори можна також додавати за правилом паралелограма: сумою векторівіє вектор—діагональ паралелограмаABCD.

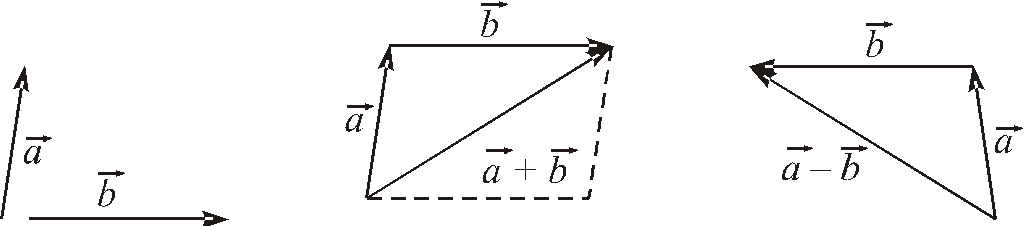
Рис. 2

Зауваження. Оскільки від будь-якої точки площини можна відкласти вектор, що дорівнює даному, то для того, щоб додати два довільно розміщені вектори, достатньо від кінця одного з них відкласти вектор, що дорівнює другому, і скористатися правилом трикутника.

Вектор-називаєтьсяпротилежним вектору . Різницею векторівіназивається сума вектораі вектора, протилежного вектору, тобто(див. рис. 2).

Теорема 3 (про єдиність розкладу вектора на площині). Нехай на площині дано два неколінеарних вектори і. Тоді будь-який третій вектору цій площині можна в єдиний спосіб подати у вигляді суми:

де х і у — числа, що називаються коефіцієнтами розкладу вектора за векторамиі.

Лема. Якщо в Δ АВС точка D лежить на стороні АС і то

Задача. Нехай у Δ АВС точка N лежить на стороні ВС, а точка М — на стороні АВ, причому BN : ВР =1 : 5; AM : АВ = 1 : 5. Прямі AN і CM перетинаються в точці О. Знайти відношення СО : МС і АО : AN (рис. 3).

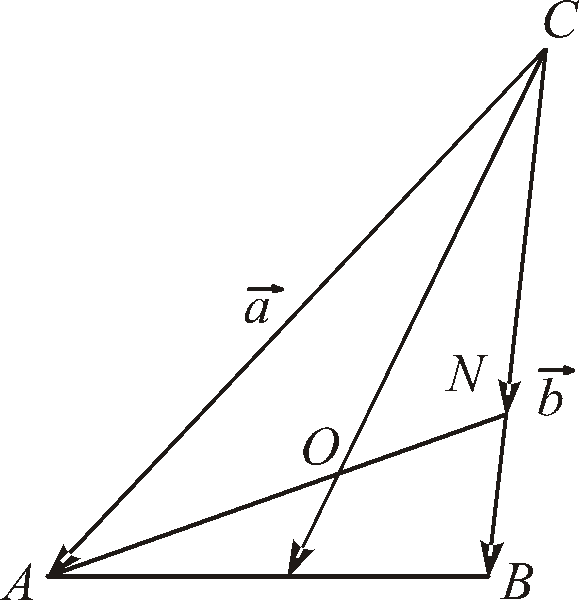
Рис. 3

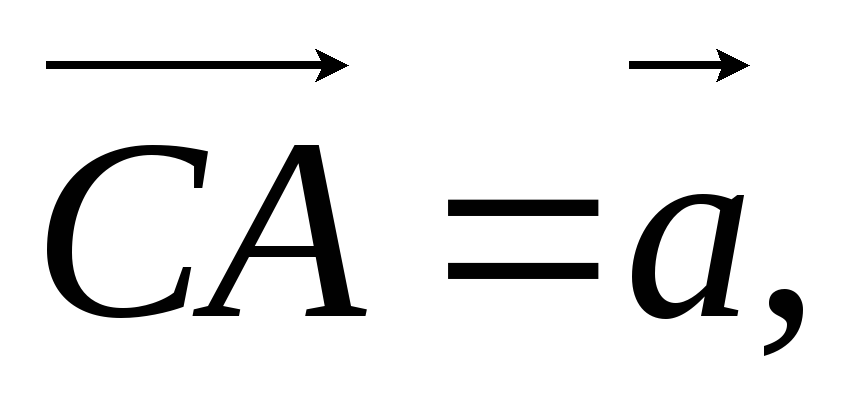
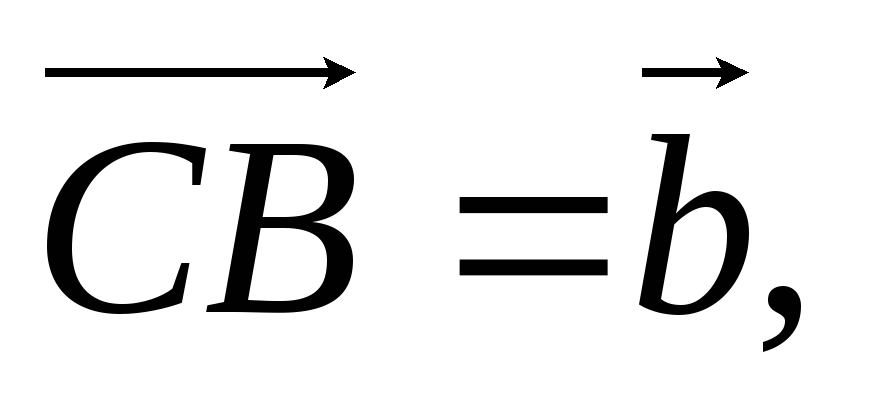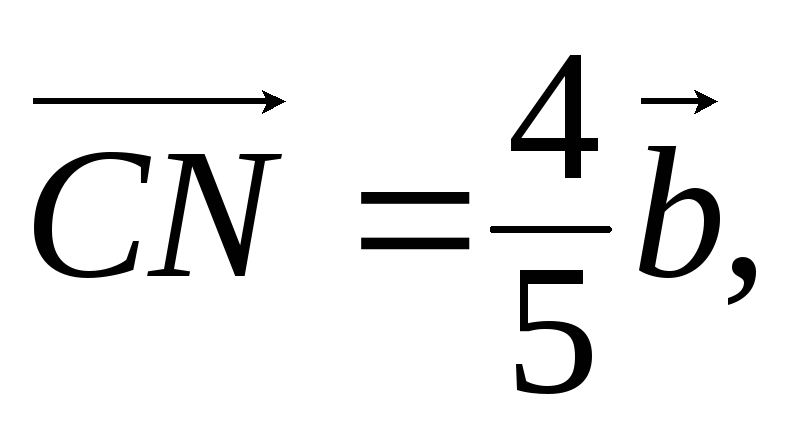
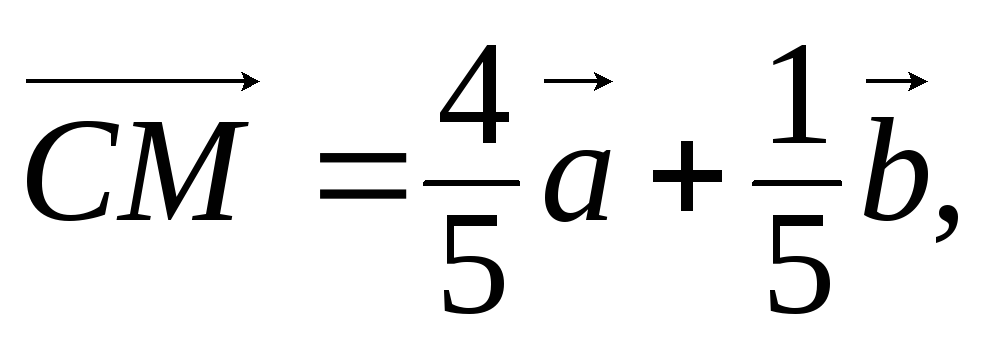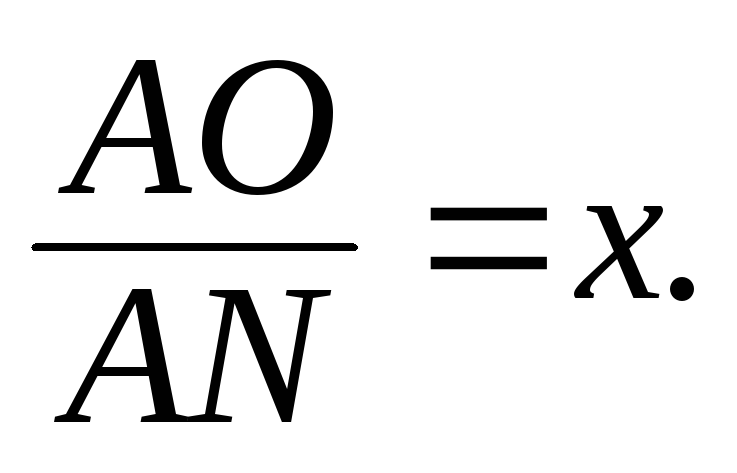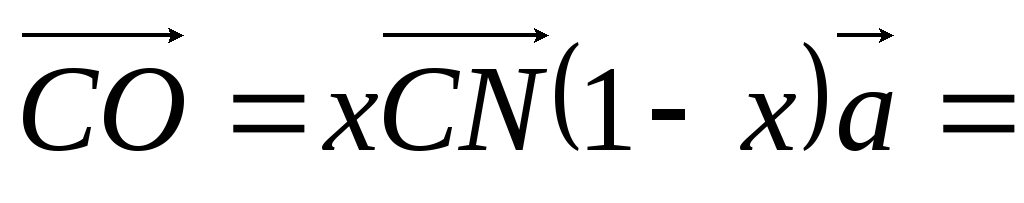
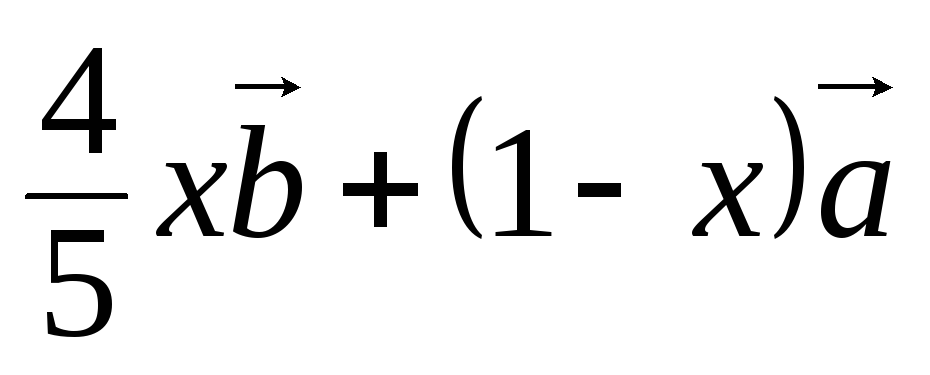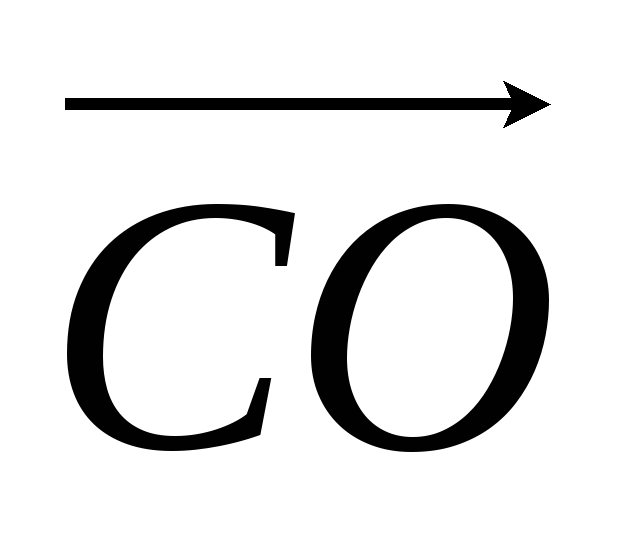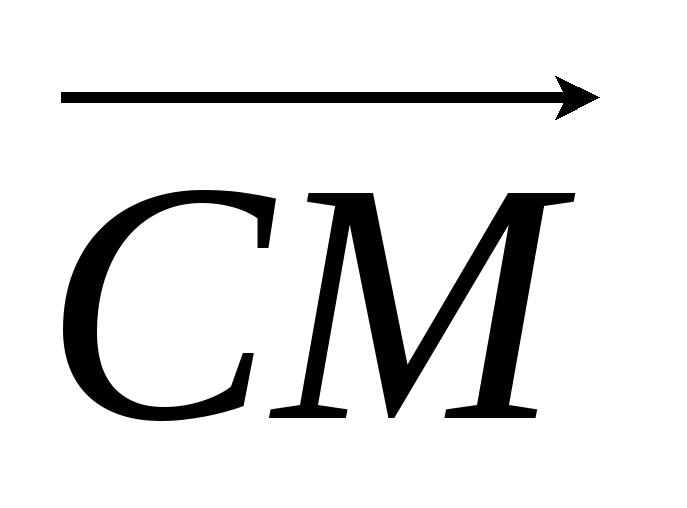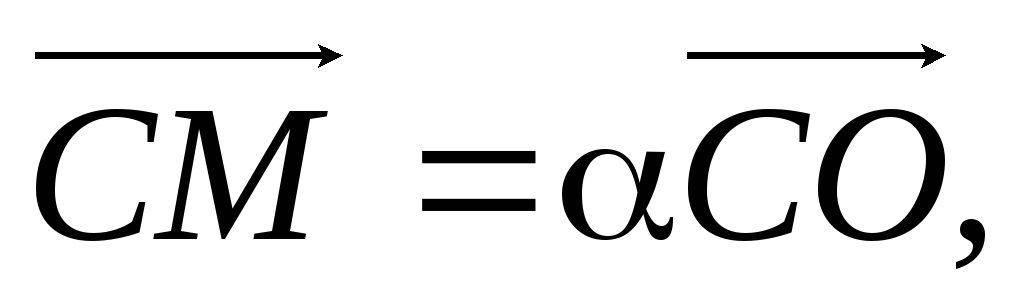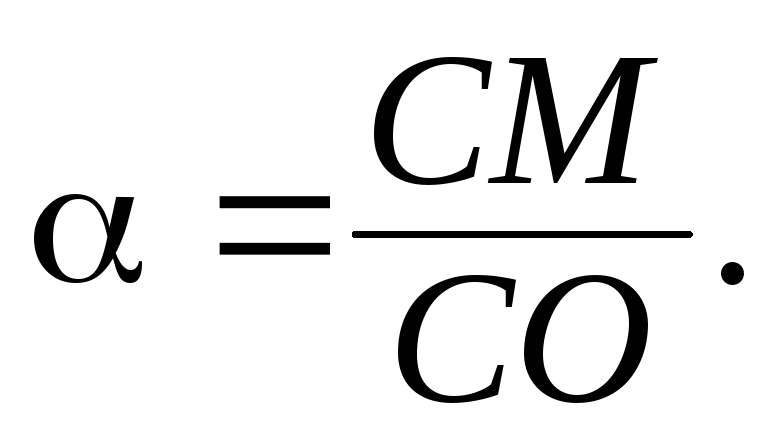• Введемо вектори тоді(за лемою). ПозначимоТоді з ΔACN за лемою дістанемо: . Оскільки век­тори іколінеарні, тодеТому.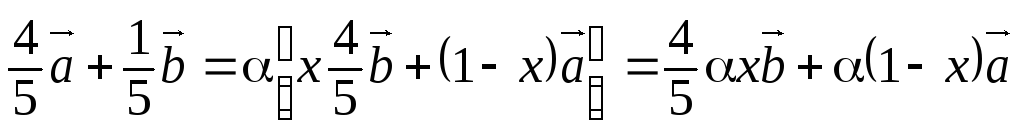

Беручи до уваги єдиність розкладу вектора за неколінеарними векторами і, маємо систему рівнянь:

Розв’язавши її, дістанемо відповідь:

16.2. Скалярний добуток векторів, його властивості

Кутом між векторами називається кут між променями, на яких лежать ці вектори.

Скалярним добутком векторів і (позначаютьабо) називається число, що дорівнює добутку довжин цих векторів, помноженому на косинус кута між ними:

(α — кут між векторами і).

Зауваження. Якщо вектори івзаємно перпендикулярні, то.

Виконуються такі властивості скалярного добутку:

l) ;

2) ;

3) .

З означення скалярного добутку випливає:

Векторний метод ефективно використовується при розв’язуванні геометричних задач.

Задача. У прямокутному трикутнику АВС AD — бісектриса ВМ — медіана трикутника (рис. 4). Знайти кут між AD і ВМ, якщо АВ = 3, ВР = 4.

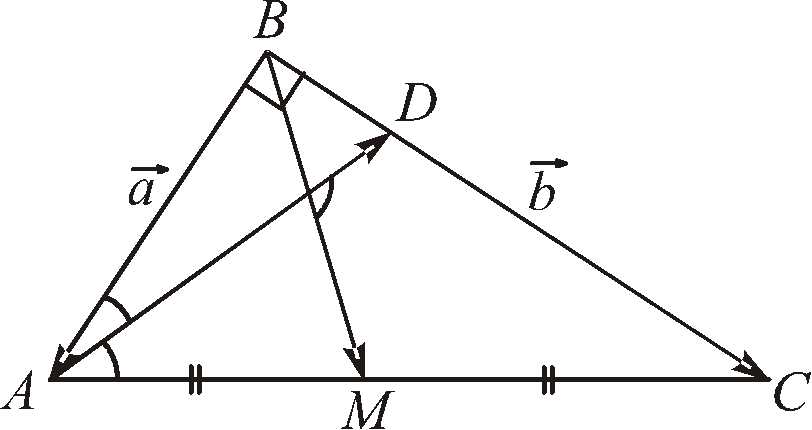
Рис. 4

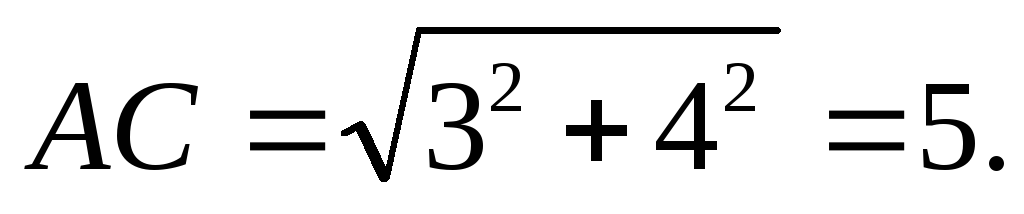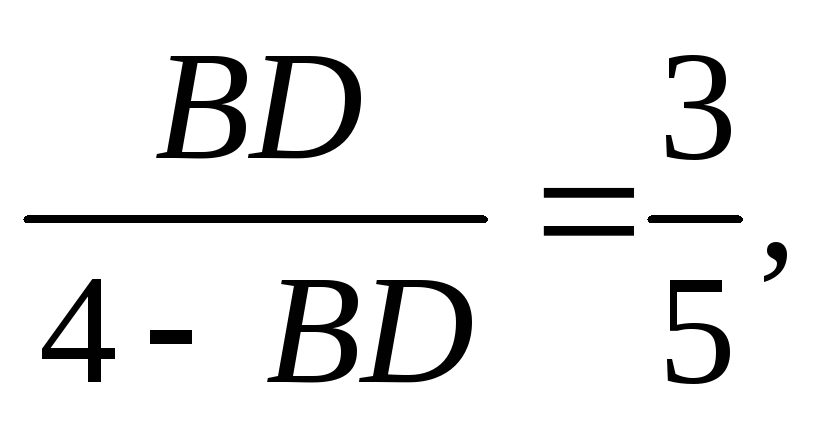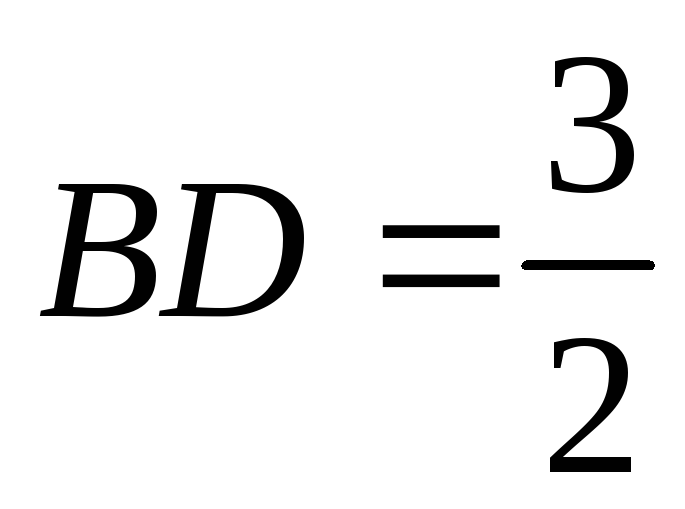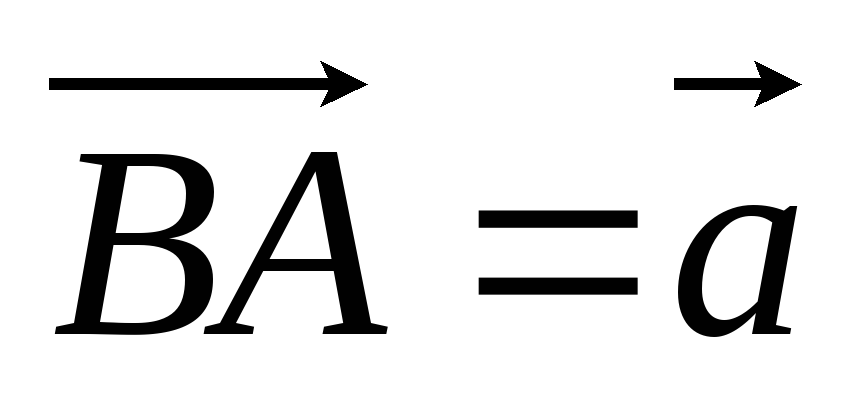• За теоремою Піфагора дістаємо Згідно з теоремою теоремі про бісектрису внутрішнього кутазвідки. Позначимо,Тоді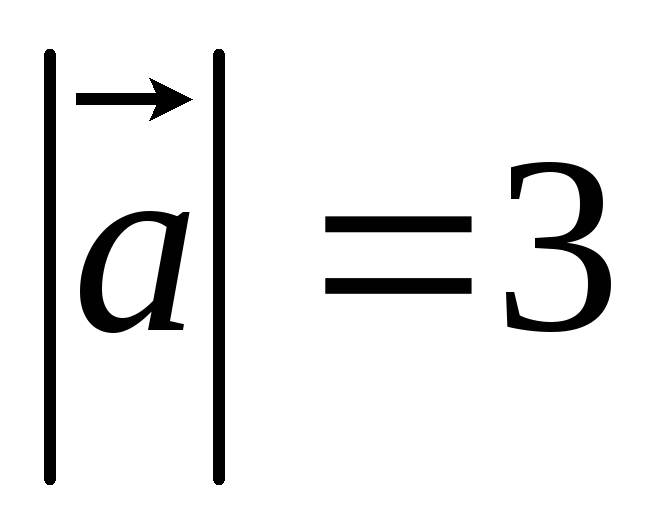,,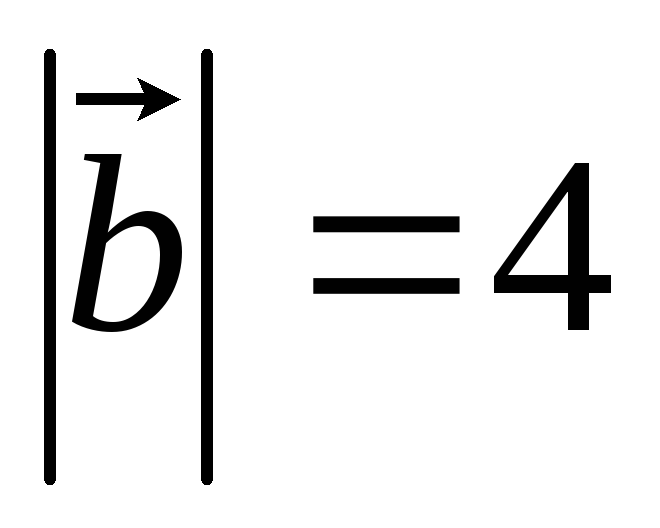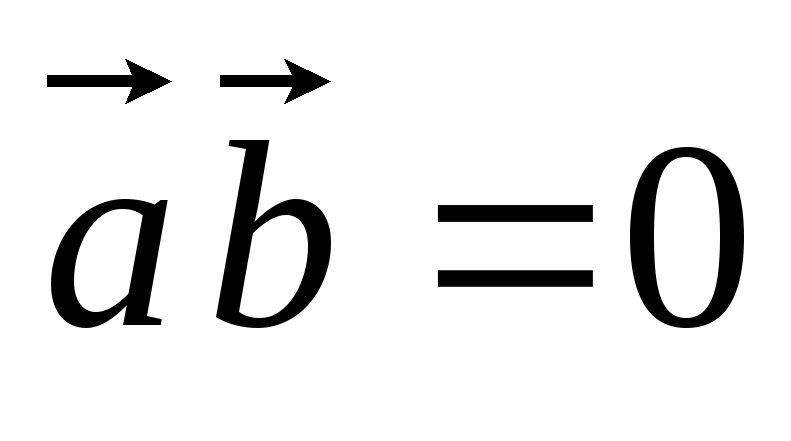. Оскільки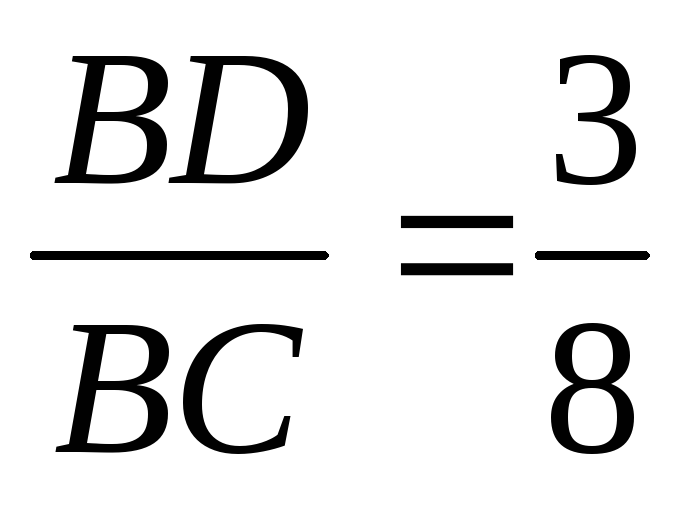, то,;.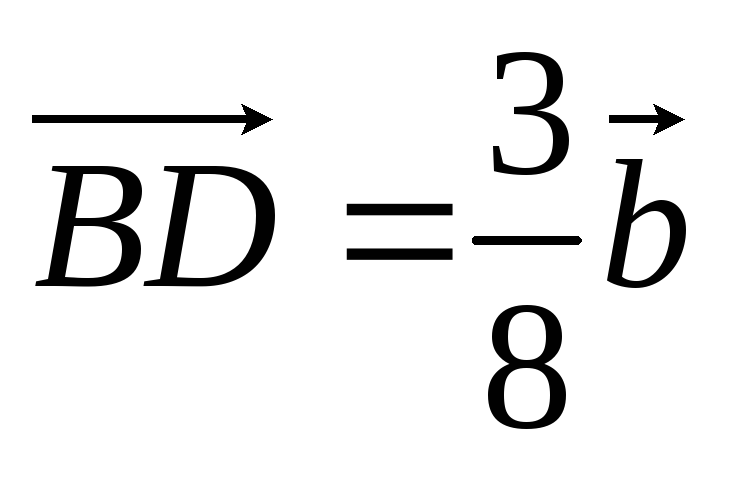

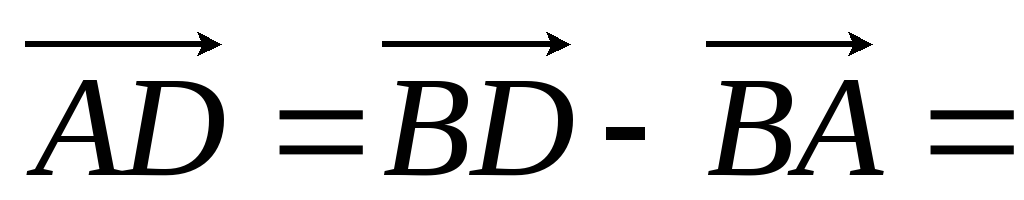
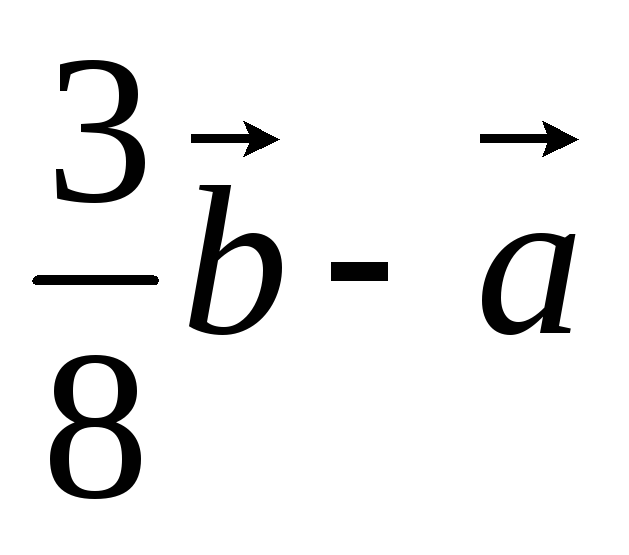Знайдемо довжину вектора :.

Враховуючи, те, що медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює половині гіпотенузи, дістаємо

Обчислюємо скалярний добуток:

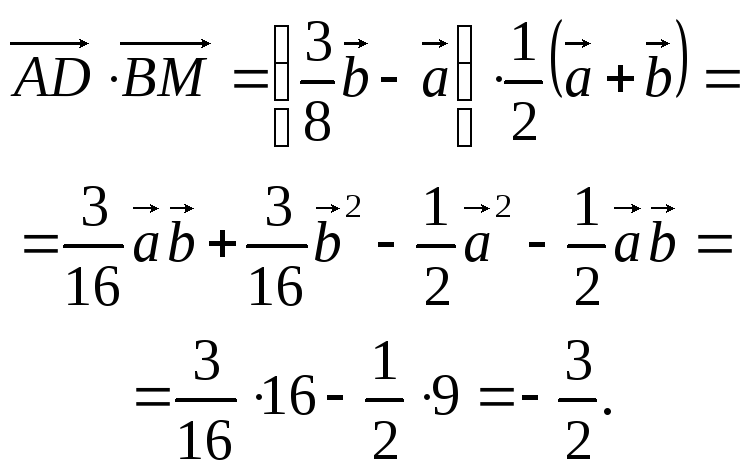
Отже,

Задача. Знайти кут між діагоналлю АС₁ і ребром AA₁ паралелепіпеда ABCDA₁B₁C₁D₁ (рис. 5), коли відомо, що AA₁ = AD = 2, АВ = 1, .

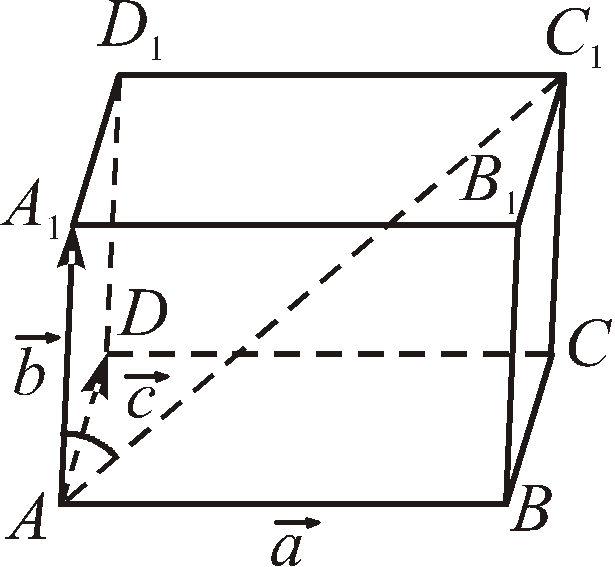
Рис. 5

• Введемо три вектори: ,,

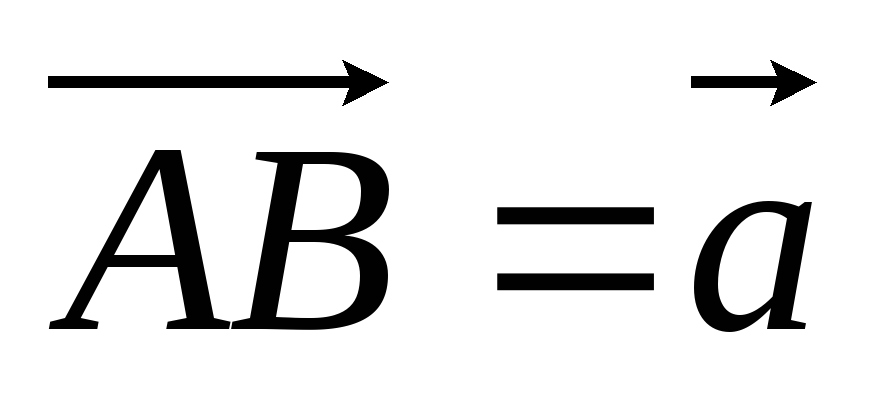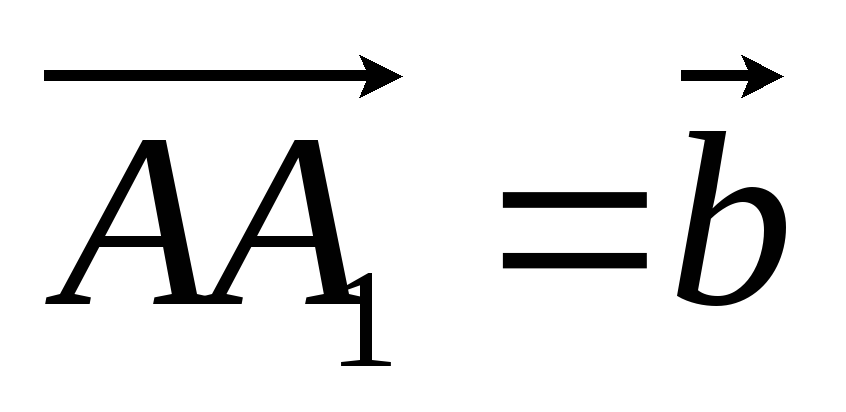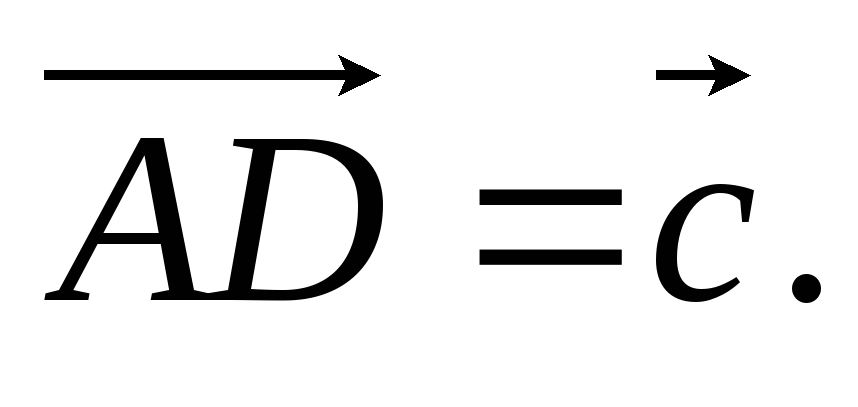
При цьому маємо:

Вектор подається через вектори,ідуже просто:

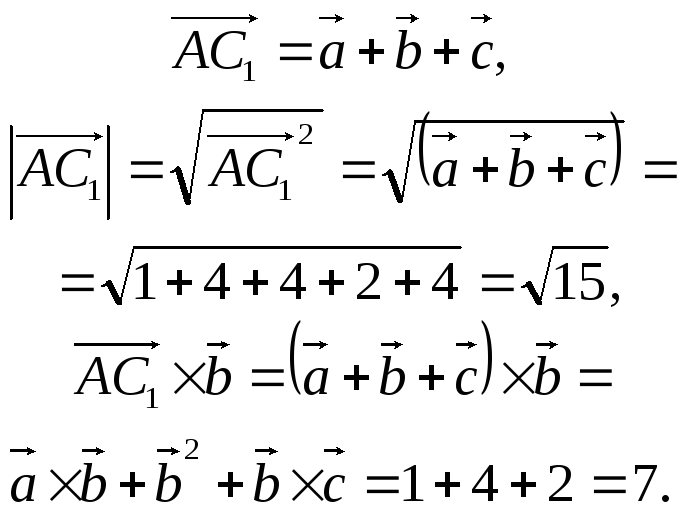
Тому

.