15.10 Циліндр. Конус. Сфера, куля та її частини

Циліндричною поверхнею називається поверхня (рис. 1), утворена рухом прямої АВ, паралельної заданому напряму l, яка перетинає дану плоску криву MN і називається напрямною цилін­дра. Пряма АВ називається твірною циліндра.

Циліндром називається тіло, обмежене циліндричною поверхнею, що має замкнуту твірну, і двома паралельними площинами. Частини паралельних площин, що обмежують циліндр, називаються основами циліндра. Висотою циліндра називається відстань h = PQ між паралельними площинами (рис. 1).

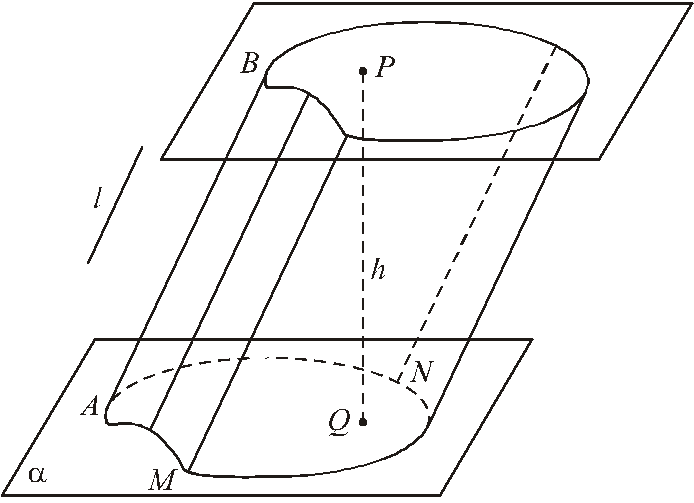
Рис. 1

Прямим циліндром називається циліндр, твірні якого перпендикулярні до основ. Циліндр називається круговим, якщо його напрямною є коло. Прямий круговий циліндр є фігурою обертання, оскільки його можна утворити обертанням прямокутника нав­коло однієї з його сторін. Пряма, що сполучає центри основ прямого кругового циліндра, називається віссю циліндра. Вона є його віссю симетрії. Площиною осьового перерізу називається площина, що містить вісь циліндра. Осьовий переріз прямого кругового циліндра являє собою прямокутник.

Площа бічної поверхні кругового циліндра радіуса r дорівнює добутку довжини кола, що лежить у його основі, на висоту цилін­дра:

S = 2πrh.

Об’єм циліндра дорівнює добутку площі основи на висоту циліндра:

V = 2πr²h.

Конічною поверхнею називається поверхня, утворена рухом прямої АВ, що проходить увесь час через ту саму точку S (вершину конуса) і перетинає дану плоску криву, що називається напрямною конуса (рис. 2, а). Твірною конуса називається будь-яка пряма, що відповідає деякому положенню прямої АВ. Конічна поверхня має дві частини: одна описується променем SA, а інша — його продовженням SB.

Конусом називається тіло, обмежене однією частиною коніч­ної поверхні, що має замкнену твірну, та площиною. Частина цієї площини, що лежить усередині конічної поверхні, називається основою конуса. Перпендикуляр SO, опущений з вершини S на площину основи, називається висотою конуса. Конус називається круговим, якщо в його основі лежить коло. Прямим круговим конусом називається круговий конус, висота h якого проходить через центр кола (точку О), що лежить в основі (рис. 2, б).

Рис. 2

Прямий круговий конус — це фігура обертання, оскільки його можна утворити обертанням прямокутного трикутника навколо одного з його катетів. Висота SO прямого кругового конуса називається також віссю конуса, вона є його віссю симетрії. Осьовим перерізом прямого кругового конуса є рівнобедрений трикутник, утворений при перетині поверхні конуса площиною, що містить його вісь. Кутом при вершині конуса називається кут при вершині його осьового перерізу.

Площа бічної поверхні прямого кругового конуса дорівнює половині добутку довжини кола основи на твірну конуса:

де r — радіус основи конуса; l — його твірна (рис. 2, б).

Об’єм конуса дорівнює одній третині добутку площі його основи на висоту:

Сферичною поверхнею, або сферою, називається геометричне місце точок простору, віддалених на однакову відстань R від однієї точки, яку називають центром сфери. Тіло, обмежене сферичною поверхнею, називається кулею. Сфера є поверхню обертання. Вона утворюється при обертанні кола навколо будь-якого його діаметра. Великим колом називається лінія перетину кулі площиною, що містить центр кулі.

Площа поверхні кулі дорівнює почетвереній площі великого круга:

Об’єм кулі

Куля називається вписаною в циліндр, якщо вона дотикається до його бічної поверхні та до площини основи. Кулю можна вписати в прямий круговий циліндр так, щоб вона мала спільну точку з будь-якого його твірною, тільки тоді, коли осьовим перерізом циліндра є квадрат. Куля називається вписаною в конус, якщо вона дотикається до бічної поверхні конуса та до площини його основи. У будь-який прямий круговий конус можна вписати кулю так, щоб вона мала спільну точку з усіма його твірними. Центр цієї кулі лежить на осі конуса.

Кульовим сегментом називається частина кулі, яку відтинає від неї будь-яка площина α. Основою кульового сегмента називається коло, утворюване в результаті перетину кулі площиною α. Висотою h кульового сегмента називається довжина відрізка МО₁, перпендикулярного до площини α (рис. 3).

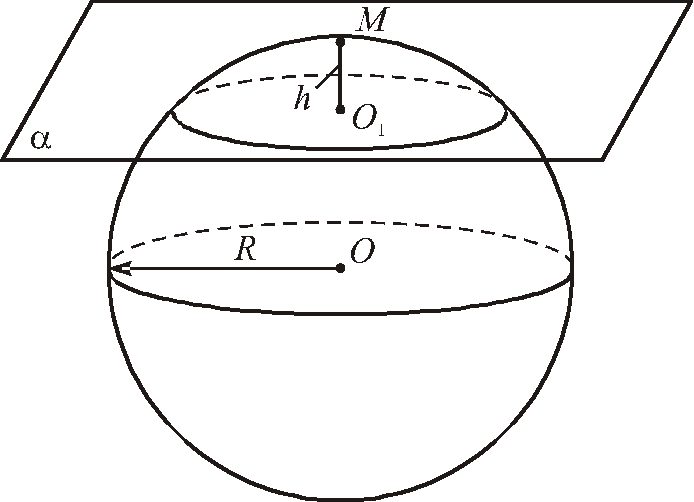
Рис. 3

Площа поверхні кульового сегмента дорівнює добутку його висоти на довжину великого кола:

S = 2πRh,

де R — радіус кулі.

Об’єм кульового сегмента

Частина кулі, що відтинається від неї двома паралельними площинами, називається кульовим шаром. Кульовим поясом, або зоною, називається поверхня кульового шару. Відстань між паралельними площинами, що називаються основами шару, має назву висоти кульового шару (рис. 4).

Рис. 4

Площа поверхні кульового шару дорівнює добутку його висоти h = О₁О₂ на довжину великого кола:

S = 2πRh.

Об’єм кульового шару обчислюють за формулою:

де r₁ і r₂ — радіуси основ кульового шару; h — його висота.

Кульовим сектором називається частина кулі, обмежена поверхнею кульового сегмента і конічною поверхнею, напрямною якої є коло основи сегмента, а вершиною — центр кулі (див. рис. 3).

Об’єм кульового сектора

де R — радіус кулі; h — висота відповідного кульового сегмента.

ЛЕКЦІЯ

ОСНОВИ ВЕКТОРНОЇ АЛГЕБРИ