15.5. Визначні точки в трикутнику

Теорема 1. Три бісектриси трикутника перетинаються в одній точці, що є центром кола, вписаного в трикутник (рис. 1).

Рис. 1

Теорема 2. Три серединних перпендикуляри, проведені до сторін трикутника, перетинаються в одній точці, що є центром кола, описаного навколо трикутника (рис. 2).

Рис. 2

Теорема 3. Три медіани трикутника перетинаються в одній точці і поділяються нею у відношенні 2 : 1, якщо лічити від вершини трикутника (рис. 3):

АТ : OK = CO : OD = 2 : 1.

Рис. 3

Теорема 4. Три висоти трикутника або їхні продовження перетинаються в одній точці, яку називають ортоцентром трикутника.

Теорема Ейлера. Точка перетину медіан, центр описаного кола та ортоцентр трикутника лежать на одній прямій, причому точка перетину медіан поділяє відрізок, що сполучає ортоцентр і центр описаного кола, у відношенні 2 : 1.

Задача. У рівнобедреному трикутнику АВС сторони дорівнюють відповідно АВ = ВР = 5, АС = 6 (рис. 4). Знайти радіус описаного кола, радіус вписаного кола і відстань між їхніми центрами.

Рис. 4

• Визначимо спочатку радіус R описаного кола. Візьмемо до уваги, що BD — висота, медіана і бісектриса трикутника АВС. Із трикутника ВВС за теоремою Піфагора визначаємо Центр описаного колаО міститься на BD; ОВ = = ОС = R; OD = 4 – OB = 4 – R. За теоремою Піфагора для трикут­ника OCD дістанемо OD² + CD² = ОС², тобто (4 — R)² + 3² = = R². Розв’язавши це рівняння, дістанемо

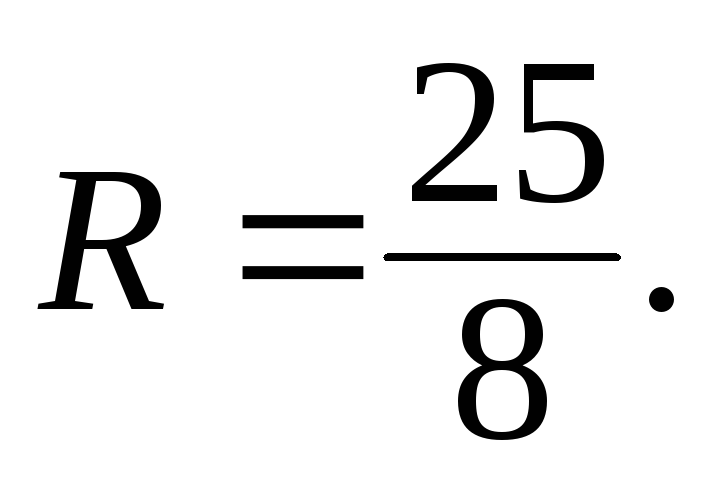
Знайдемо тепер радіус r уписаного кола. Маємо: BD — бісектриса кута АВС; СО₁ — бісектриса кута ВСА. Точка О₁ — центр уписаного кола, O₁D = r, ВО₁ = 4 – r. За теоремою про бісектрису внутріш­нього кута для трикутника ВВС маємо звідки

Обчислюємо відстань між центрами кіл: О₁О = О₁D – OD = r – – (4 – r) =  

Теорема Морлі. Якщо в довільному трикутнику кожний кут поділити на три рівні частини, то точки перетинану променів, що поділяють кути цього трикутника (рис. 5, а), є вер­шинами рівностороннього трикутника.

Таку саму властивість мають і точки перетину променів, що поділяють на рівні частини зовнішні кути довільного трикутника (рис. 5, б).

Рис. 5

15.6. Метричні теореми планіметрії. Формули площі трикутника

Теорема Піфагора. Якщо трикутник прямокутний, то сума квадратів катетів дорівнює квадрату гіпотенузи:

а² + b² = c²,

де а = ВC, b = AC, c = АВ (рис. 1).

Рис. 1

Обернена теорема: Якщо сума квадратів двох сторін трикутника дорівнює квадрату третьої сторони, те цей трикутник прямокутний.

За допомогою теореми Піфагора доводяться наведені далі твер­дження.

1. У рівнобедреному прямокутному трикутнику гострі кути дорівнюють по 45°, а відношення гіпотенузи до катета дорівнює

2. Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.

Для прямокутного трикутника (див. рис. 1):

• синус гострого кута дорівнює відношенню катета, протилежного цьому куту, до гіпотенузи;

• косинус гострого кута дорівнює відношенню катета, прилеглого до цього кута, до гіпотенузи;

• тангенс гострого кута дорівнює відношенню катета, протилежного цьому куту, до катета, прилеглого до нього.

Таким чином, згідно з рис. 1 маємо:

Теорема косинусів. Квадрат сторони трикутника дорівнює сумі квадратів двох інших його сторін мінус подвоєний добуток цих сторін на косинус кута між ними (рис. 2):

с² = а² + b² – 2abcos γ.

Теорема синусів. Відношення сторони трикутника до синуса протилежного кута є величина стала для даного трикутника, що дорівнює двом радіусам описаного кола (рис. 2):

Рис. 2

Задача. У трикутнику дано три сторони а, b, с. Знайти довжину медіани, проведеної до сторони а.

• Нехай ADC = φ, AD = m_a — медіана Δ АВС (рис. 3). Маємо ADB = 180° — φ. Запишемо теорему косинусів для трикутників ADC і ADB:

Рис. 3

Додавши ці рівняння почленно і врахувавши рівність cos (180° – – φ) = –cos φ, дістанемо:

Після елементарних перетворень знайдемо

Теорема. У будь-якому трикутнику сума квадратів медіан дорівнює суми квадратів сторін трикутника.

Формули для обчислення площі трикутника (рис. 2)

(1)

(2)

(3)

(4)

(5)

де h_a — висота, опущена на сторону a; r — радіус уписаного кола; R — радіус описаного кола; р — напівпериметр. Формула (5) називається формулою Герона.

Зауваження. Якщо формула Герона дає надто громіздкий вираз, то площу можна обчислити за формулою (2), де

За допомогою метричних теорем і формул для площі трикутника можна розв’язати будь-яку задачу типу: Дано три елементи трикутника, принаймні один з яких є мірою довжини. Знайти будь-який інший елемент трикутника.

Задача. Дано три сторони трикутника: а, b, с. Знайти кут α, висоту h_a, радіуси описаного (R) і вписаного (r) кіл та площу S трикутника.

• Маємо а² = b² + с² – 2bccos α, звідки

2. Згідно з формулою вираження (1) знаходимо Підставляючи сюдиS із формули (5), дістаємо:

де

3. Використовуючи формулу (4), знаходимо деS обчислюється за формулою (5).

4. За формулою (3) дістаємо де S визначається за формулою (5).

Наведемо ще кілька корисних метричних співвідношень у довільному трикутнику:

;

;

;

;

відстань між центрами вписаного та описаного кіл

Площа чотирикутника

де d₁ і d₂ — довжини діагоналей чотирикутника; α — кут між ними.

Площа паралелограма

де γ — кут між суміжними сторонами а і b.

Площа трапеції

де а і b — основи трапеції; h — її висота.