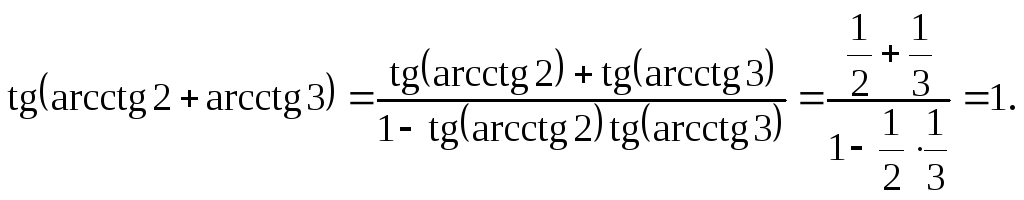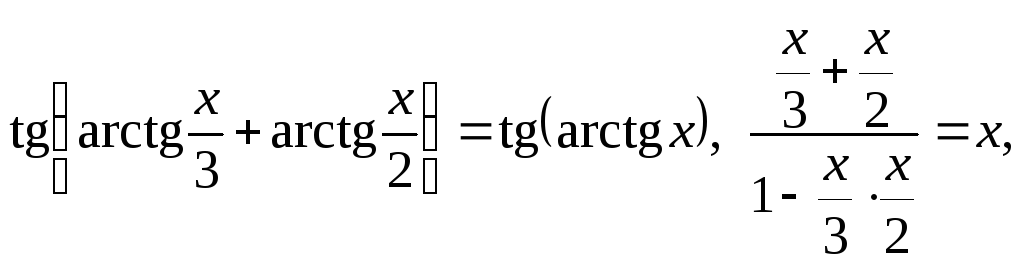учебное пособие / лекція 7

ЛЕКЦІЯ

ОБЕРНЕНІ ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ

7.1. Обернена функція

Нехай функція неперервна і монотонна на інтервалі і при цьому змінна набуває значень на інтервалі . Розв’язавши рівняння відносно , знайдемо розв’язок .

Функція називається оберненою до функції .

За зазначених умов обернена функція існує і неперер­вна при . При цьому виконуються рівності:

, ; ₍₁₎

, .

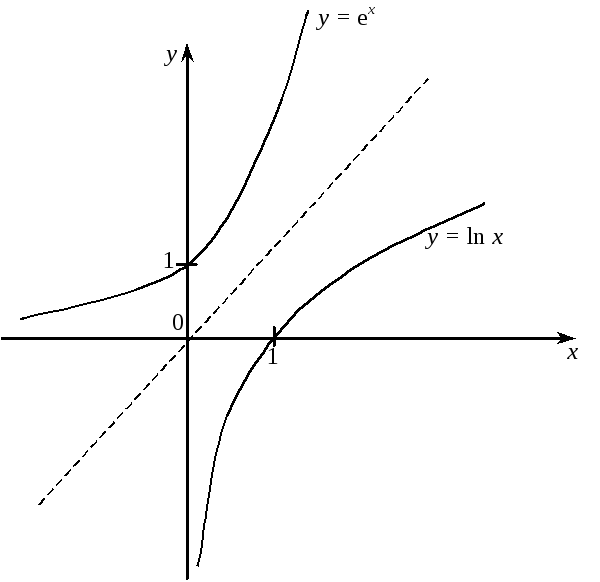
Графіки функцій , симетричні відносно бісек­триси першого координатного кута.

Наприклад, функція , визначає залежність між змінними , яку можна також подати рівнянням , . Скориставшись позначеннями , подамо рівності (1) у вигляді:

, ; ₍₂₎

, .

Графіки функцій , симетричні відносно бісектриси першого координатного кута (див. рисунок).

7.2. Графік і властивості функції y = arcsin x

Функція неперервна і монотонна при . Обернена до неї функція , , називається арксинусом (див. рисунок).

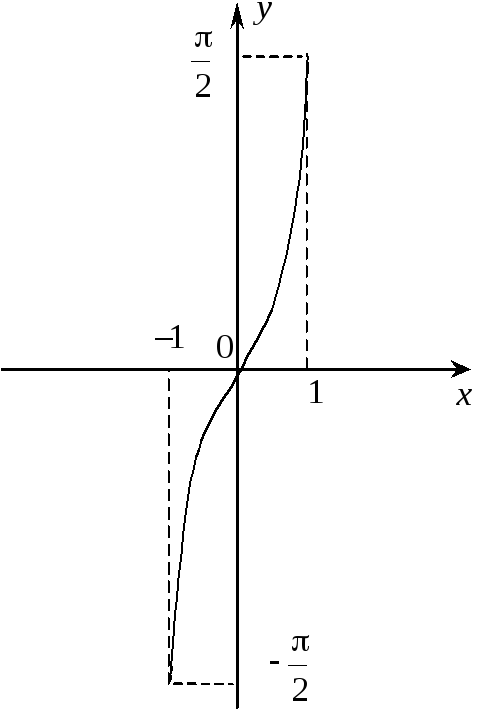
Функція монотонно зростає на відрізку і задовольняє такі нерівності:

. (1)

Арксинусом називається кут, що задовольняє нерів­ності (1) і синус якого дорівнює :

, . (2)

Наведемо деякі числові значення функції :

; ; ; (3)

; .

Функція — непарна, тобто

. (4)

Корисно запам’ятати такі формули:

, ;

, ; (5)

, ;

, , .

Приклад. Обчислити .

• Виконуємо обчислення:

.

Приклад. Розв’язати нерівність .

• Маємо: 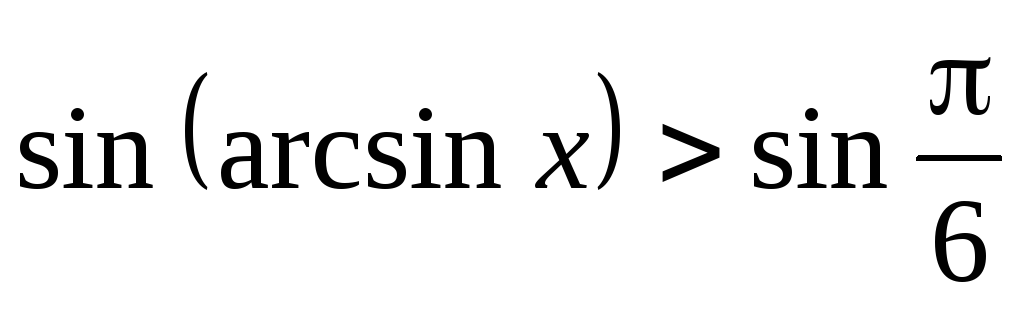; . Оскільки , то остаточно дістаємо: .

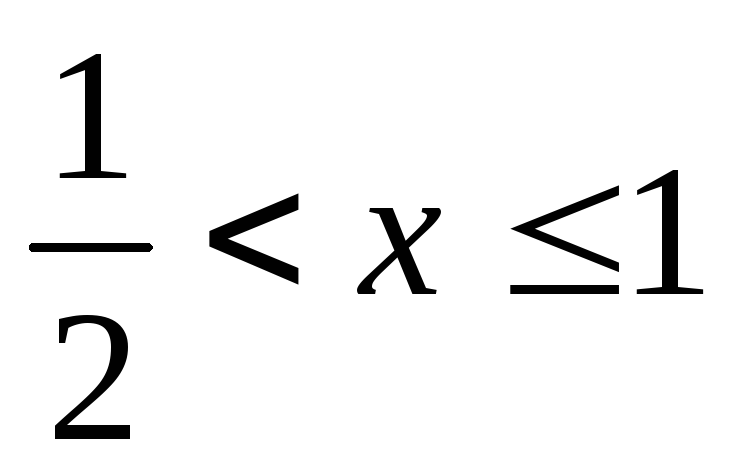7.3. Графік і властивості функції y = arccos x

Функція неперервна і монотонна при . Обер­нена до неї функція , , називається арккосинусом (див. рисунок).

Функція монотонно спадає на відрізку і задовольняє такі нерівності:

. (1)

Арккосинусом x називається кут, що задовольняє нерівності (1) і косинус якого дорівнює :

, . (2)

Із симетрії графіка відносно точки випливає рівність:

,

звідки знаходимо формулу

. (3)

Порівнюючи графіки функцій і , діста­ємо:

, . (4)

Наведемо деякі числові значення :

; ; ;

; . (5)

Корисно запам’ятати такі формули:

, ;

, ;

, ,

, . (6)

Приклад. Обчислити значення функції .

• 

.

Приклад. Обчислити значення функції .

• .

7.4. Графік і властивості функції y = arctg x

Функція неперервна і монотонна при . Обернена до неї функція , , називається арк­тангенсом (див. рисунок).

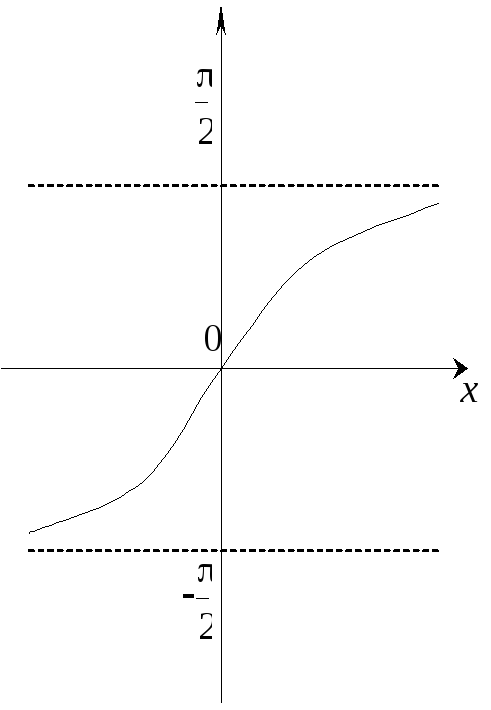
Функція монотонно зростає, непарна і задовольняє нерівності:

. (1)

При цьому виконуються граничні співвідношення:

, . (2)

Арктангенсом x називається кут, що задовольняє нерівності (1) і тангенс якого дорівнює :

, . (3)

Функція набуває таких значень:

, , ; (4)

, .

Корисно запам’ятати деякі формули:

; ,

; , (5)

; ,

; , .

Приклад. Обчислити значення .

• .

Приклад. Обчислити значення суми .

• .

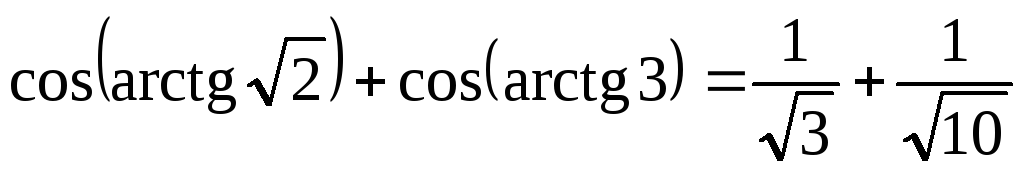Виведемо формулу для суми арктангенсів.

Нехай справджується рівність .

Знаходимо значення

.

Звідси маємо:

. (6)

Оскільки виконуються нерівності (1), то число k може набувати значень , .

Приклад. Знайти значення суми .

.

Приклад. Знайти значення суми .

• .

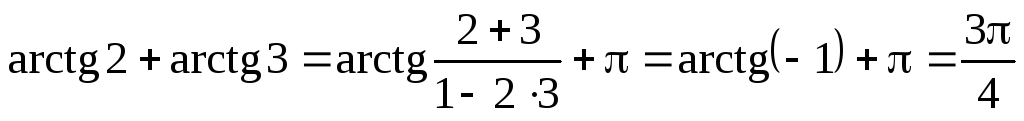7.5. Графік і властивості функції y = arcctg x

Функція неперервна і монотонна на проміжку . Обернена до неї функція називається арккотангенсом (див. рисунок).

Функція монотонно спадає і задовольняє нерівності:

. (1)

При цьому виконуються граничні співвідношення:

. (2)

Арксотангенсом x називається кут, що задовольняє нерівності (1) і котангенс якого дорівнює :

, . (3)

Розглядаючи графіки арктангенса і арккотангенса, доходимо висновку, що завжди виконуються рівності:

; (4)

. (5)

Наведемо табличні значення арккотангенса:

; ; ;

; . (6)

Корисно запам’ятати такі формули:

, ,

, , (7)

, , ,

, .

Приклад. Обчислити значення функції.

• 

.

Приклад. Обчислити значення функції .

• 

Розглянемо складніші приклади обчислення значень обернених тригонометричних функцій.

Приклад. Знайти вираз для суми .

• Нехай . Тоді ,

, .

Остаточно маємо:

.

Приклад. Обчислити .

• 

.

Приклад. Обчислити .

• .

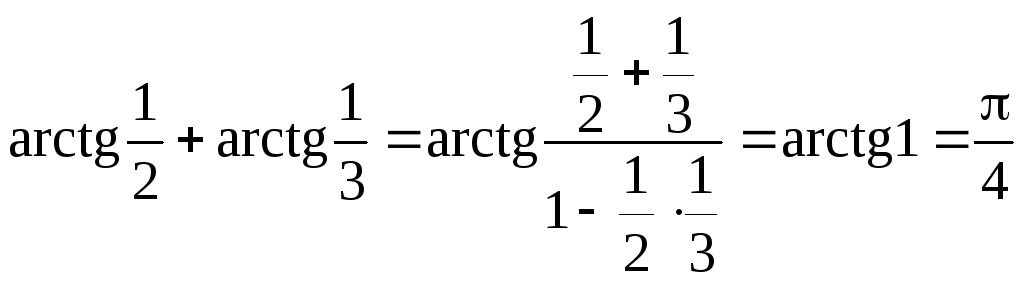Приклад. Обчислити .

• 

;

, , .

Приклад. Обчислити .

• Позначимо , тоді

,

, .

Приклад. Обчислити .

• За формулою для суми арктангенсів знаходимо:

;

;

.

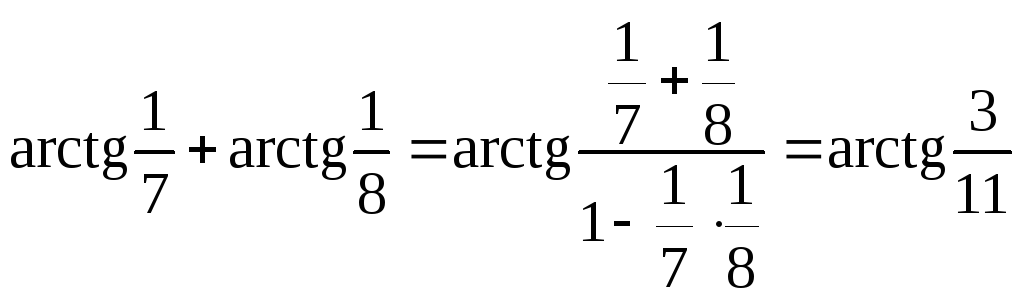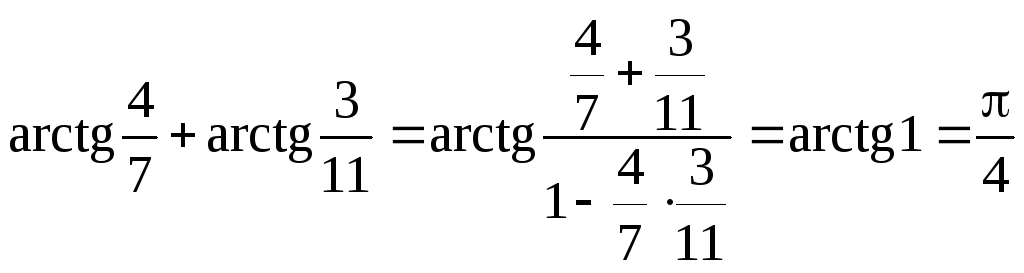Приклад. Обчислити .

• Позначимо 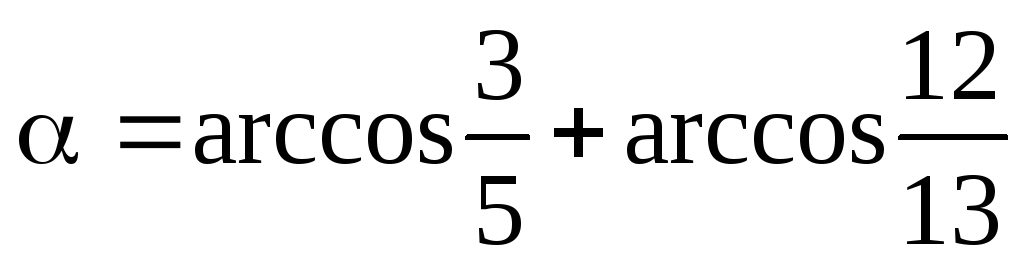. Тоді

, ; .

7.6. Рівняння з оберненими тригонометричними функціями

Розв’язуючи рівняння з оберненими тригонометричними функ­ціями, застосовують тригонометричні функції.

Приклад. Розв’язати рівняння .

• , , звідки .

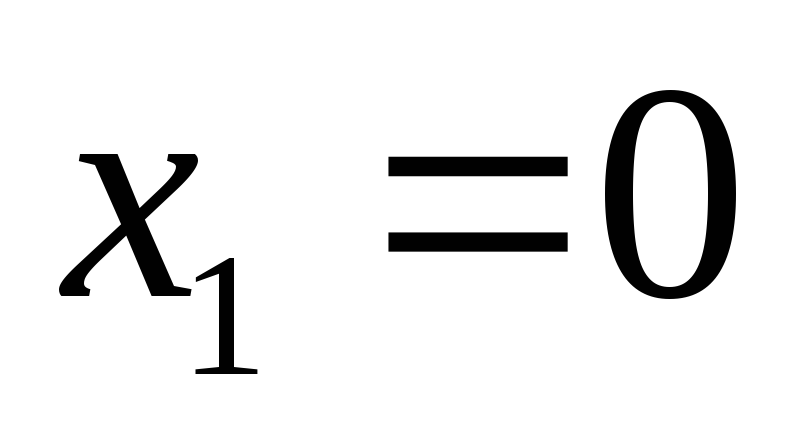Варто перевірити корені рівняння . Доходимо виснов­ку, що числа також є коренями вихідного рівняння.

Приклад. Розв’язати рівняння .

• Позначивши 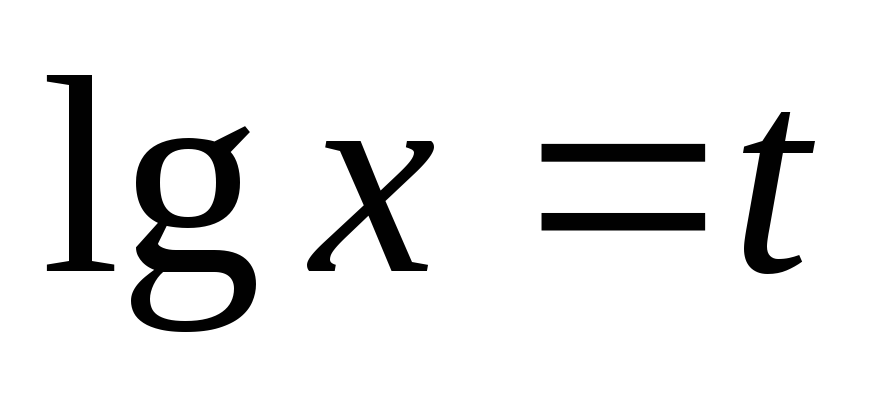, дістанемо рівняння

. Застосуємо функцію до обох частин рівняння:

, ;

, , .

Другий розв’язок не задовольняє рівняння.

Отже, маємо:, .

Приклад. Розв’язати рівняння: .

• , , ;

, , , .

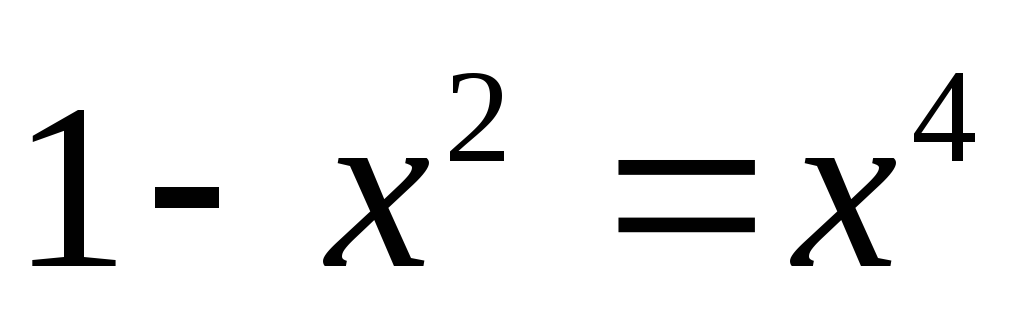Розглядаємо два випадки:

1. рівняння 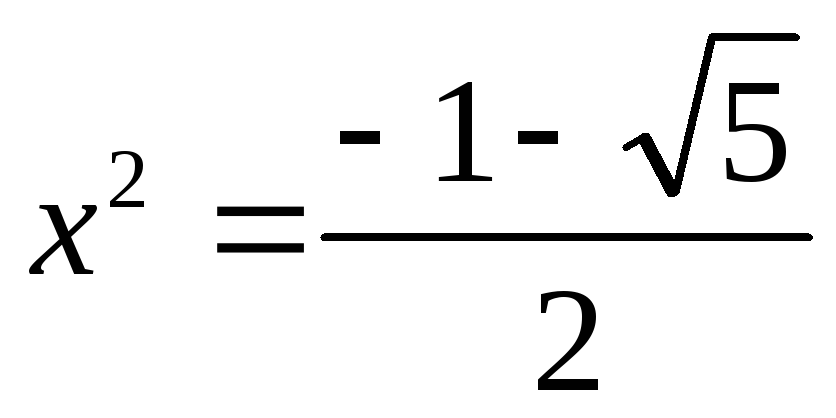не має розв’язків;

2. , , .

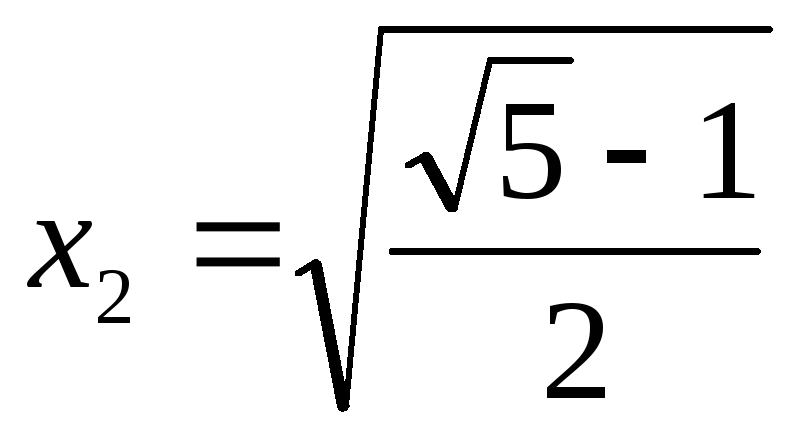Розв’язок не задовольняє рівняння, оскільки

, .

Отже, маємо.

Приклад. Розв’язати рівняння .

• Використовуємо тотожність 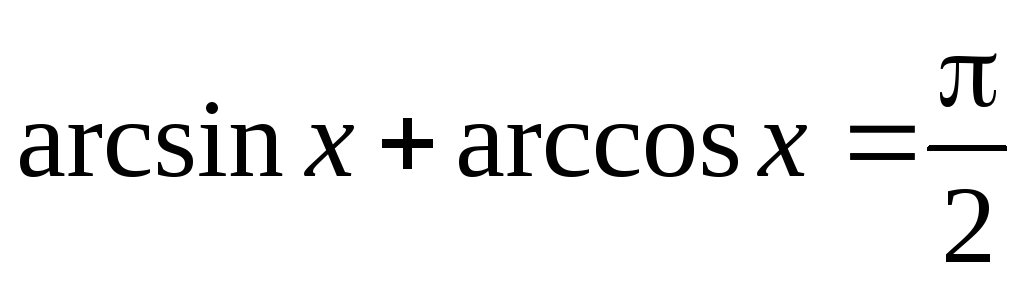; arcsin x = t, ;

; , , ;

, , .

Приклад. Розв’язати рівняння .

• ; , ,

, , .

Розв’язок не задовольняє вихідне рівняння.

Приклад. Розв’язати рівняння

• 

Приклад. Розв’язати рівняння

.

• 

Приклад. Розв’язати рівняння

• 

217

Елементарна математика