18. Степенные ряды, теорема Абеля.

Степенным рядомназывается функциональный ряд(1), т.е., где- центр ряда (1),- числа, называемые коэффициентами ряда (1). Если, то ряд имеет вид.

Th. Для рядавозможен только один из следующих случаев: 1) Ряд- сходится на числовой прямой. 2) Ряд- сходится прии расходится при. 3)ряд- сходится на интервале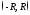и расходится вне отрезка.

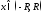Док-во: Проведем лишь для случая конечный или бесконечный приделдокажем что он. Воспользуемся признаком сходимости Даламбера для отрицательного ряда.. Предположим, что, т.е., тогда- ряд расходится. Если, то. По признаку Даламбера ряд- расходится. Т.об., в случае когдаR– конечное число ряд- сходится абсолютно наи расходится вне отрезка. - ■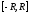

19. Интегрирование и дифференцирование функциональных рядов.

Th. Степенной рядможно почленно дифференцировать и интегрировать внутри интервальной сходимости. Это означает, что для его суммысправедливы равенства:

1) (1); 2)(2).

Док-во: Докажем формулы (1) и (2). Предположим, что конечный или бесконечный придел. Тогда степенной ряд в правой части формулы (1) имеет радиус сходимости. Аналогично, степенной ряд в формуле (2), т.е. рядимеет радиус сходимости. Т.об., ряды полученные формальным дифференцированием и интегрированием степеней рядаимеют тот же радиус сходимости ряда. Докажем формулу (1). Пусть. Выберемтак, чтобы выполнялось включение. Очевидно, что всегда можно сделать так. Т.к.R– радиус сходимости рядови (1), то по следствию изThАбеля рядыи (1) – сходятся равномерно нарядможно почленно дифференцировать на этом отрезке. Для данной точки х выполняется (1). Т.к. х выбрано произвольно из интервала сходимости, то формула (1) справедлива на всем интервале. Формула (2)изthо почленном интегрировании равномерно сходящихся рядов, поскольку ряд- сходится равномерно на отрезке.- ■

20. Ряд Тейлора и ряд Маклорена.

Пусть функция определена в некоторой окрестностии имеет производные всех порядков, в точке. Тогда степенной ряд виданазываетсярядом Тейлорадля функции.

В случае ряд Тейлора называетсярядом Маклоренадля функции.

Решим теперь общий вопрос о разложении данной функции f(x) в ряд по возрастающим целым степеням х.

.

Пусть, например, f(x) представима в виде ряда

. (3.1)

Следовательно, необходимо определить коэффициенты а₀,а₁,а₂,...; причем интервал сходимости не сводится к точке, то есть R>0.

Учтем то, что степенной ряд (3.1) в интервале сходимости можно почленно дифференцировать любое число раз и все полученные таким образом ряды тоже будут сходиться, а их суммы равны соответствующим производным.

Продифференцируем последовательно ряд (3.1):

f^/(x) = a₁ + 2×a₂×x + 3×a₃×x² + ...

f^//(x) = 2×a₂ + 2×3×a₃×x + 3×4×a₄×x² + ...

f^///(x) = 2×3×a₃ + 2×3×4×a₄×x + 3×4×5×a₅×x² + ...

f^IV(x) = 2×3×4×a₄ + 2×3×4×5×a₅×x + ...

........................................................................

Положим теперь в этих равенствах и в (3.1) х = 0; тогда получим, что

f(0) = a₀; f^/(0) = a₁; f^//(0) = 2×a₂; f^///(0) = 2×3×a₃; f^IV(0) = 2×3×4×a₄; ...

То есть а₀ = f(0); ;;;; ...

Подставляя эти значения в (3.1), получим ряд Маклорена:

.

Мы знаем, что в некоторых случаях f(x) или ее производная неопределенны при х = 0: так, например, ведут себя функции f(x) = ln(x), , для которыхили. Следовательно, такие функции не могут быть разложены в ряд Маклорена. Тогда нужно воспользоваться более общими степенными рядами.

Рассмотрим разложение в степенной ряд функции f(x) по степеням (х-а), где а¹0 и его можно подобрать соответствующим образом так, чтобы

f(x) = А₀ + А₁×(х - а) + А₂×(х - а)² + ... . (4.1)

Для (10.1) справедливо.

Пусть х - а = z.

Тогда разложение (4.1) примет вид

F(z) = f(z + a) = А₀ + А₁×z + А₂×z² + ... , (4.2)

где . Но это уже ряд Маклорена.

Так как F⁽ⁿ⁾(z) = f⁽ⁿ⁾(z + a), (n=1,2,...).

Таким образом, имеем

A₀ = F(0) = f(a), , ...,, ...

Подставив эти выражения в (10.2), получим ряд Тейлора

. (4.3)

Если а = 0, получим ряд Маклорена.

Если в (4.3) взять конечное число членов, то вместо ряда Тейлора получим многочлен Тейлора

. (4.4)

То есть если (4.3) сходится в некоторой окрестности точки а (U_a), то его сумма равна f(x), a P_n(x) дает приближенное представление f(x) в U_a.

23. Показательная функция, тригонометрическая функция комплексной переменной.

Под элементарными функциями комплексных переменных понимают функции, которые можно представить в как сумму степенного ряда по степеням комплексных переменных z.

1. 

2. Показательная функция

Естественно определим, что и для комплексных переменных должно быть разложение в такой же ряд

В частности для чисто мнимого аргумента zполучим

Выделим отдельно мнимые и действительные части

-формула Эйлера.

.

0. Тригонометрическая функция

В результате разложения в ряд следующих функции ,можно заметить следующее:

Из системы находим и.

…

Отметим, что является периодической с периодом;- также являются периодическими с периодом.

Пример.

24. Логарифмическая и степенная функция комплексной переменной.

Под элементарными функциями комплексных переменных понимают функции, которые можно представить в как сумму степенного ряда по степеням комплексных переменных z.

1. 

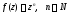
   1. Логарифмическая функция

Пусть ,

- эта функция многозначная.

-главное значение логарифма.