16. Знакопеременные(знакочередующиеся) ряды. Теорема Лейбница. Абсолютная и условная сходимость числового ряда.

Знакочередующийся ряд– ряд вида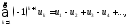гдеили ряд вида

Th(признак Лейбница). Пусть(1) – знакочередующийся ряд такой, что послед. неотрицат. чиселмонотонно убывает и, тгда ряд- сходится. Кроме тогоn-тый остаток рядаудовлетворяет неравенству(2) или, т.е. сумма остатка ряда по модулю не превышает последовательного отброшенного члена ряда.

Док-во: Рассмотрим частичную суммы четного порядка . Т.к. послед.- убывает, то все члены в скобках неотрицательные. Кроме того суммаполучена из суммыдобавлением неотрицательного слагаемогопоследовательностьмонотонно возрастает, с другой стороны запишемв виде. Все члены в скобках неотрицательные и кроме того(3) . Т. об., последовательность- монотонно возрастает и ограничена сверху числом, поэтомуконечный придел. Для сумм нечетного порядка имеем. По условию придел, то. Т. об., суммы четного и нечетного порядка, стремятся к одному и тому же числу, т.е. ряд- сходится. Докажем формулу (2). Из формулы (3). Рассмотримn-тый остаток, ряд (1) нечетного порядка 2n-1. Рассмотрим остаток ряда (1) четного порядка 2n. Ряд- есть знакочередующимся рядомего суммаудовлетворяет неравенству. Для суммы нечетного порядка можно доказать, что- неотрицательное. - ■

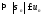Таким образом, все ряды можно разбить на два класса:

1. К первому классу сходящихся рядов отнесем ряды, которые сходятся сами, и при этом ряды, составленные из абсолютных величин их членов, тоже сходятся - это так называемые абсолютно сходящиеся ряды.

2. Ко второму классу отнесем ряды, которые сходятся сами, но при этом ряды, составленные из абсолютных величин их членов, расходятся - это так называемые условно сходящиеся или неабсолютно сходящиеся ряды.

Если сходится ряд , то рядабсолютносходится.

Th1 (абсолютная сходимость числового ряда). Если ряд абсолютно сходится, то он и просто сходится, т.е. если сходится ряд из модулей членов данного ряда, то сходится и данный ряд.

Док-во: Пусть задан ряд (1) члены произвольного знака. Рассмотрим ряд(2). Обозначими- частичные суммы ряда (1) и (2). Для произвол. натурального числаnиpимеем. Т. об., имеем(3). Т.к. ряд (2) – сходится, то последовательностьудовлетворяет критерию Коши для последовательности. Т.е.можно указать натуральныйтак , что при всехвыполняется неравенство. Из (3)что послед.удовлетворяет критерию Коши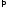сходится, т.е. ряд (1) – сходится. - ■

Th1 (условная сходимость числового ряда(Римана)). Пусть ряд- сходится условно и пустьd- произвольное число, тогда члены рядаможно представить таким образом, что сумма полученных в результате перестановки рядасовпадают с числом А. Кроме того, можно указать такую перестановку членов ряда, при котором получим в результате этой перестановки рядбудет расходится.

17. Функциональные последовательности и ряды. Область сходимости функционального ряда. Равномерная сходимость, признак равномерной сходимости.

Функциональной последовательностьюназывается бесконечная последовательность вида, членами которой являются функции, при этом считаем, что каждая функция, задана на некотором одном и том же множестве Х и принимает значение вR, т.е.числовая функция.

Областью сходимости функциональнойпоследовательностиназывается множество всех элементов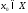, при которых сходится числовая последовательность. Обозначается.

Очевидно, что .

Пусть задана функциональная последовательность , где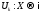- числовые функции, тогдафункциональным рядомназывается ряд вида(1).

Ряд (1) сходится, при некотором . Если этот х принадлежит области сходимости функциональной последовательности, т.е. если при данном х сходится числовой ряд. Множество всех х, при которых ряд (1) – сходится, называетсяобластью сходимости ряда. Обозначается.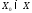

Последовательностьравномерно сходитсяв функции, еслиможно указать натуральноетакое, что при всехвыполняется.

()

Рядсходится равномернона множестве Х в своей сумме, если последовательность его частичных суммсходится равномерно.

Th(признак Вейерштрасса равномерной сходимости). Пусть задан функциональный рядивыполняется, тогда если числовой ряд- сходится, то ряд- сходится равномерно на Х.

Док-во: Возьмем , т.к. ряд- сходится, тоимеемрядудовлетворяет критерию равномерной сходимости Коши, поэтому сходится равномерно на Х. - ■