29.Уравнения с разделяющимися переменными.Диф.Уравнения в полных дифференциалах.Интегрирующий множитель.
Уравнения с разделёнными переменными. Так называются уравнения вида
f(x) dx + g(y) dy = 0. (10)
Пусть
y(x)
- решение этого уравнения, т.е. f(x)dx
+ g(y(x))dy(x)
= 0. Интегрируя это тождество, получим
- общий интеграл (общее решение) этого
уравнения.
Пример:
решить задачу Коши
Исходное уравнение - с разделёнными
переменными, интегрируя его, получим
.
Соотношение (x-1)2
+ y3
= C
- общее решение (общий интеграл) уравнения;
для того, чтобы найти частное решение,
удовлетворяющее начальному условию,
надо подставить в общее решения данные
значения x0
и y0,
и найти значение постоянной C
на этом решении: (2-1)2
+ 13
= 2
C
= 2. Таким образом, решение поставленной
задачи: (x-1)2
+ y3
= 2.
Уравнения с разделяющимися переменными. Так называются уравнения вида
(11)
или f1(x) g1(y) dx + f2(x) g2(y) dy = 0 . (12)
Эти уравнения легко сводятся к уравнению с разделёнными переменными:
|
Записываем
уравнение (11) в форме
|
|
Уравнение
(12) делим на f2(x)
g1(y):
|
|
Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы: | ||
|
|
|
|
|
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному. | ||
|
Если функция g(y) имеет действительные корни y1, y2, y3, …, то функции y = y1, y = y2, y = y3, …, очевидно, являются решениями исходного уравнения. |
|
Если функция f2(x) имеет действительные корни корни x1, x2, x3, …, функция g1(y) имеет действительные корни y1, y2, y3, …, то функции x = x1, x = x2, x = x3, …, y = y1, y = y2, y = y3, … являются решениями исходного уравнения. |
|
В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши. | ||
,
затем делим наg(y)
и умножаем на dx:
.
.
.
.
Примеры:
1.
.
При
такой форме записи общего интеграла
решение y
= 1 потеряно. Можно преобразовать общее
решение к виду, который содержит это
решение. Переобозначим постоянную C
как ln|C1|:
.
Вернёмся
к обозначению постоянной интегрирования
C;
общее решение
содержит частное решениеy
= 1 при C
= 0.
2.
Найти решение задачи Коши
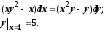
Решаем
уравнение:
.
Здесь
могут быть потеряны решения
постоянная интегрирования записана
как
.
Далее,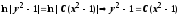
.
Общий интеграл уравнения
y2
= C(x2
– 1) + 1. Частные решения
содержатся в общем интеграле приC
= 0, решения
утеряны (понятно, почему это произошло:
если записать уравнение в форме, решённой
относительно производной,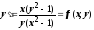
,
то, очевидно, на решениях
нарушаются условия, налагаемые теоремой
Коши на правую часть уравнения). Всё
множество решений:
y2 = C(x2 – 1) + 1, x = 1, x = -1. Мы должны найти ещё частное решение, удовлетворяющее начальному условию y(1) = 5. Подстановка значений x = 1, y = 5 в общий интеграл даёт 25=1, т.е. общий интеграл этого частного решения не содержит. Решение x = 1 удовлетворяет начальному условию, это и есть решение задачи Коши.
К
уравнениям с разделяющимися переменными
сводятся уравнения вида
(
- постоянные). Если перейти к новой
неизвестной функцииz
= ax
+ by
+ c,
то
,
и уравнение представляется как
.
Это - уравнение с разделяющимися
переменными.
Пример:
.
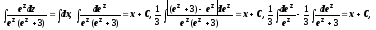
Уравнение в полных дифференциалах. Так называется уравнение вида
P(x, y) dx + Q(x, y) dy = 0, (16)
(P(x,
y),
Q(x,
y)
- непрерывно дифференцируемы) в случае,
если его левая часть является полным
дифференциалом некоторой функции u(x,
y),
т.е. если существует такая функция u(x,
y),
что
.
Необходимым и достаточным условием
существования такой функции является
условие
.
Если (16) - уравнение в полных дифференциалах,
то его правая часть равна
,
т.е. (16) принимает видdu(x,
y)
= 0. На решении y(x)
получим
du(x, y(x)) = 0, следовательно, u(x, y(x)) = C, где C - произвольная постоянная. Соотношение
u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
Для
нахождения функции u(x,
y)
решается система уравнений
Из первого уравнения этой системы
находим
с точностью до произвольной дифференцируемой
поy
функции
(эта функция играет роль постоянной
интегрирования; так как интегрирование
ведётся по переменнойx);
затем из второго уравнения определяется
.
Пример:
найти общее решение уравнения
.
Убедимся, что это - уравнение в полных
дифференциалах. Здесь
;
,
т.е. это действительно уравнение
рассматриваемого типа. Ищем функциюu(x,
y)
такую, что
Из
первого уравнения
.
Дифференцируем эту функцию поy
и приравниваем выражению, стоящему во
втором уравнении системы:
.
Если мы правильно решаем это уравнение
(т.е. правильно определили его тип и
правильно выполнили предыдущие действия),
то в полученном уравнении для
должны остаться только члены, зависящие
отy.
Действительно, представляя
как
,
получим
.
Следовательно,
,
и общее решение уравнения имеет вид
.
31.Линейные ДУ уравнения первого порядка. Уравнение Бернулли.
ДУ
первого порядка называется линейным,
если неизвестная функция y(x)
и её производная
входят в уравнение в первой степени:
. (14)
Здесь p(x), q(x) - непрерывные функции.
Для
решения уравнения (14) представим y(x)
в виде произведения двух новых неизвестных
функций u(x)
и v(x):
y(x)
= u(x)
v(x).
Тогда
,
и уравнение приводится к виду
,
или
.
Это уравнение решаем в два этапа: сначала
находим функциюv(x)
как частное решение уравнения с
разделяющимися переменными
;
затем находимu(x)
из уравнения
.
Итак,
(мы не вводим в это решение произвольную
постояннуюC,
нам достаточно найти одну функцию v(x),
обнуляющую слагаемое со скобками в
уравнении
).
Теперь уравнение дляu(x)
запишется как
.
Общее решение уравнения (14): 
.
Запоминать эту формулу не надо, лучше усвоить порядок действий и воспроизводить его при решении каждой задачи.
Пример:
.
Решение:
.
Теперь для u(x)
получим:
,
и
общее решение уравнения
.
Для нахождения частного решения,
соответствующего начальным условиям
задачи Коши, подставим в общее решение
.
Решение задачи:
.
Этот
метод решения линейных уравнений часто
реализуется по-другому - в форме вариации
произвольной постоянной. Уравнение
(14) называется однородным, если q(x)
= 0. Пусть дано неоднородное уравнение
(14)
.
Оно, как и в предыдущем случае, решается
в два этапа. Обнулим правую часть,
получившееся уравнение будем называть
однородным уравнением, соответствующим
уравнению (14):
.
Решаем это уравнение:
(при
делении на y
теряется решение y
(x)
= 0, но оно входит в общее решение при C
= 0). Теперь ищем общее решение уравнения
(14) в виде
,
где
-
новая неизвестная функция; находим
производную
и подставляем в (14)y
и
:
,
или
,
где
.
Теперь
.
Понятно, что обе реализации решения имеют один смысл (решение однородного уравнения играет роль функции v(x), варьируемая постоянная C(x), - роль функции u(x),).
Отметим ещё одно важное обстоятельство. Переменные x и y, входящие в уравнение, равноправны, поэтому при определении типа уравнения надо иметь в виду, что может оказаться предпочтительней искать решение в виде x = x(y), а не в виде y = y(x).
Пример:
(x
+ y2)dy
= ydx.
Если мы представим это уравнение в виде
,
то решить его не сможем, так как оно не
принадлежит ни одному из рассмотренных
типов. Если же представить его в виде
,
то относительно функцииx
= x(y)
оно линейно. Решаем его методом вариации
произвольной постоянной. Соответствующее
однородное уравнение:
. Его решение:
.
Ищем решение данного уравнения в форме
x
= C(y)
y.
Тогда
(постояннаяC0
переобозначена как
).
Утерянное решение -y
= 0.
Уравнение Бернулли. Так называется уравнение
, (15)
где
(приm
= 0 уравнение линейно, при m
= 1 - с разделяющимися переменными). Это
уравнение решается одним из следующих
способов:
1.
Уравнение Бернулли сводится к линейному
подстановкой z
= y1-m
(при m>1
может быть потеряно решение y
= 0). Действительно,
,
.
После деления уравнения (15) наym
получим
,
или
- линейное уравнение.
Пример:
(уравнение Бернулли,m
= 2).
Подстановка
.
Решаем полученное линейное уравнение:
.
2.
Можно сразу решать уравнение Бернулли
методом, которым решаются линейные
уравнения, т.е. заменой y(x)
= u(x)
v(x):
из
этого выражения находимu(x),
и y(x)
= u(x)
v(x).
Пример:
решить задачу Коши
Как и в предыдущем примере, это уравнение
не попадает ни под один из рассмотренных
типов: оно не является ни уравнением с
разделяющимися переменными (наличие
суммыx2
+ y),
ни уравнением с однородной правой частью
(слагаемые разных порядков - первого и
второго в этой сумме), ни линейным, ни
Бернулли (другая структура). Попробуем
опять представим это уравнение как
уравнение относительно x
= x(y):
Это уже уравнение Бернулли сm
= -1. Начальное условие примет вид x(1)
= 2. Решаем уравнение:
.
Тогда
.
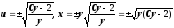Это общее решение уравнения (утерянное
решение
y
= 0 не удовлетворяет начальному условию).
Ищем частное решение, удовлетворяющее
начальному условию:
;
решение задачи Коши:
.
32. Линейные однородные ДУ второго порядка с постоянными коэффициентами.
