12. Объем тела и объем тела вращения. Площадь поверхности вращения.

В пространстве задано некоторое тело. Оно расположено между двумя плоскостями. Плоскости пересекают ось Ох в т. а и в. Известен закон изменения плоскости сечения данного тела плоскости к оси Ох. Найдем объем этого телаV.

Разбиваем отрезок точками, получим разбиение. Через т.поводим плоскостик оси Ох, обозначим их. Выбираем т.. Заменяем часть тела лежащую между плоскостямиицилиндром. Высотой, а основание цилиндра представляет собой фигуру полученную в сечении тела плоскостьюоси х и проходящей через т.. Заменяем все тело ступенчатой фигурой получим изn-цилиндров написанных выше.

Перейдем к приделу при , получим точное значение объема:

Функция - непрерывна на, тогда при вращении фигуры, а АВ в вокруг оси х образуется некоторое тело круглой тело, которое назыв.тело вращения.

При произвольном в сечении тела вращения имеем круг радиуса

13. Несобственный интеграл 1-го и 2-го рода.

Несобственные интегралы 1 рода-.

Введем определения для несобственных интегралов 1 рода.

Определение 1.

Если предел конечен, то несобственный интеграл 1 рода называется сходящимся;

Если предел бесконечен или не существует вовсе, то несобственный интеграл 1 рода называется расходящимся.

Свойства несобственных интегралов.

а) Признак сравнения несобственных интегралов 1 рода. Если 0 меньше (или равен) f(x) меньше (или равна) g(x) на промежутке [0;+ ], то:

Из сходимости следует сходимость.

Из расходимости следует расходимость.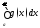

Теорема очевидна из геометрического смысла.

б) Признак абсолютной сходимости несобственного интеграла 1 рода.

Если несобственный интеграл 1 рода сходится, то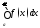тоже сходится.

Следует из первого свойства.

Несобственные интегралы 2 рода.

Определение 1.

Интеграл вида: , где y=f(x) непрерывна (a;b], a - точка разрыва 2 рода, называется несобственным интегралом 2 рода.

Если предел конечен, то несобственный интеграл 2 рода называется сходящимся.

Определение 2.

Если предел равен бесконечности или не существует вовсе, то несобственный интеграл 2 рода называется расходящимся.

Пусть функция y=f(x) имеет разрыв 2 рода в точке C, принадлежащей (a;b). В остальных точках промежутка непрерывна.

Определение 3.

Если оба несобственных интеграла 2 рода справа сходятся, то несобственный интеграл слева называется сходящимся.

Если хотя бы один из интегралов справа расходится, то несобственный интеграл слева называется расходящимся.

Свойства несобственных интегралов 2 рода те же, что и для несобственных интегралов 1 рода.

14. Числовые ряды, положительные числовые ряды, сумма ряда, необходимое условие сходимости ряда, основные теоремы о числовых рядах.

Пусть задана числовая последовательность .

Формальная сумма бесконечного числа слагаемых назывчисловым рядом, при этом- общий член ряда.

Сумма первых n– членов назывn - той частичной суммой ряда. Обозначается.

Ряд - сходится, если последовательность частичных сумм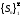имеет конечный приделS, который назывсуммой ряда.Ряд сходится, есликонечный предел.

Если последовательность частичных сумм ряда не имеет конечного предела, то ряд расходится.

Св-ва сходящихся рядов:

1. Сходящиеся ряды можно почлено складывать. Если ряды и, то ряд- сходятся, и при этомтакже для обычных сумм.

Док-во: Для конечной суммы n-слагаемыхпереходя к приделу получим требуемое.

Или

Для любого конечного числа N , но

и согласно условию теоремы. Тогда

- ■

2. Постоянную можно выносить за знак суммы ряда. Если ряд -сходитсяk– некоторое число, то ряд-сходится, при этом.

Док-во:

Так как , то имеем, что- ■.

3. Если ряд сходится, то и любой его r-остаток также сходится..

Док-во: Пусть r– некотороеNчисло, тогда при любыхn>rимеем, чтои при этом справедливо равенство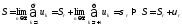. Полученную формулу можно записать в виде- ■.

Th(необходимое условие сходимости для произвольного ряда): Если рядсходится, то. Общий член сходящегося ряда.

Док-во: Пусть частичная сумма ряда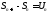. Так как ряд сходится, то. – ■

Следствие. Если общий член ряда не , то ряд расходится. Обратное утверждение не верно. Т. е. если общий член ряда, это еще не значит- ряд расходится, хотя.