10. Площадь плоской фигуры, уравнение которой задано в явном виде, параметрическими уравнениями, в полярных координатах.

Площадь плоской фигуры, уравнение которой задано в явном виде

Пусть функция у = f(x) определена, непрерывна и неотрицательна на отрезке [а; b], тогда плоская фигура, ограниченная дугой графика функции на этом отрезке и прямыми х = а, х = b, у = 0, называется криволинейной трапецией. Площадь криволинейной трапеции определяется по формуле: .

Площадь «сложной» фигуры Под «сложной» фигурой будем понимать часть плоскости, ограниченную непрерывными на отрезке [а; b] кривыми

у = f(x) и у = g(x) (f(x) g(x), x[а; b]) и прямыми х = а,

х = b. Площадь «сложной» фигуры находится по формуле:

.

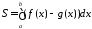Распространенной является постановка задачи о площади плоской фигуры, ограниченной двумя кривыми. Предполагается, что эти кривые, пересекаясь, образуют некоторую ограниченную фигуру. В этом случае пределы интегрирования (х = а, х = b) заранее не известны и должны быть определены из решения системы уравнений:

Если задача поставлена корректно, то эта система имеет два решения, которые определяют координаты точек пересечения кривых.

Площадь фигуры, ограниченной параметрически заданной кривой

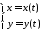
Пусть - параметрическое уравнение кусочно-гладкой простой замкнутой кривой, проходимой против часовой стрелки. Тогда формула площади ограниченной данной кривой фигуры имеет вид:

Если при изменении параметра t от 0 до Т кривая проходит по часовой стрелке, то в этих формулах необходимо сменить знак на противоположный.

Площадь плоской фигуры, уравнение которой задано в полярных координатах

Площадь сектора, ограниченного непрерывной кривой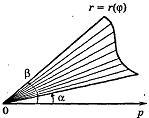

r = r() и лучами=;=(<), равна

Площадь сегмента, ограниченного непрерывными кривыми r = r() и р = р() и лучами=;=(<), равна

11. Длина дуги кривой, уравнение которой задано в явном виде, параметрическими уравнениями, уравнениями в полярных координатах.

Равенство 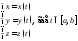назывпараметрическим уравнением кривой, а переменнаяt– параметром. Точка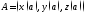назыв началом кривой,- концом кривой. Аналогично определяется плоская кривая с помощью равенств.

Кривая lназыв замкнутой, если ее начало совподает с концома=в. Криваяlназыв непрерывно дифференцируемой, если функциинепрерывно дифференцируема на отрезкена.

Рассмотрим плоскую кривую lи поставим вопрос о вычислении ее длинны. Возьмем разбиениеотрезок. Это разбиение имеет вид,. Каждой точкесоответственно точка кривой. Соединив т.,отрезками прямых получим ломанную. Она вписана в кривуюl. Каждому разбиениюотрезкасоответствует ломаная вписана в кривуюl. Обозначим- длину этой ломанной, где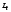- положительное число, которое соответствует всякому разбиению.

Кривая lназывспрямляемой, если(т.е.), при этом сам приделназывдлиной кривой.

Th: (вычисление длинны кривой (заданная в явном виде)) Пустьlнепрерывно дифференцированная плоская кривая, заданная уравнением, тогда криваяlспрямляема и ее длина вычисляется по формуле.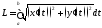

Док-во: Возьмем . Пусть- длинная вписанная ломаная, тогда имеем. Применим формулу Лагранжа к функциии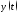, тогда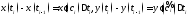, где- некоторые точки из интеграла, получим:(1). Правая часть (1) похожа на интегральную сумму функции А, но ей не является, т.к.. Покажем, что сумма в формуле (1) стремится прик тому же приделу, что и интеграл суммы, т.е. к интегралуиз (1), что кривая иlспрямляема и ее длина имеет вид- ■.

Th: Длина дуги заданной явным уравнением (2).

Док-во: Дугу AB произвольным образом разделим на n-частей, с точками: . Через точкипроведем отрезки, при этом -.

Интегральная сумма для длины дуги.

- ■.

Вычисление дуги AB заданной параметрически

Задача: Найти длину дуги, если AB:

Имеет место формула: (2')

Док-во: Используем формулу (2)

Сокращая, получаем формулу (2'). Вычисление длины дуги AB заданной в полярной системе координат. Выражение под знаком интеграла в формуле (2) равно и называется дифференциалом длины дуги.

Используя связь между ПСК и ДПСК, получаем:

(2'').