
- •Математический анализ
- •1. Отображение множеств (функции). Область определения функции. Монотонные функции. Четные и нечетные функции. Периодические функции.
- •2. Предел последовательности. Предел суммы, разности, произведения. Предел функции на бесконечность, предел функции в точке. Замечательные пределы.
- •3. Непрерывность функции. 1-а и 2-а теоремы Больцано-Коши, 1-а и 2-а теоремы Вейерштраса.
- •5. Основные теоремы дифференциального исчисления Ферма, Ролля, Лагранжа и Коши.
- •6. Экстремум функции. Выпуклость функции, точки перегиба.
- •7. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица неопределенных интегралов.
- •8. Интегрирование при помощи переменной и по частям.
- •9. Определенный интеграл. Формула Ньютона-Лейбница. Условие интегрирования функции.
- •10. Площадь плоской фигуры, уравнение которой задано в явном виде, параметрическими уравнениями, в полярных координатах.
- •11. Длина дуги кривой, уравнение которой задано в явном виде, параметрическими уравнениями, уравнениями в полярных координатах.
- •12. Объем тела и объем тела вращения. Площадь поверхности вращения.
- •13. Несобственный интеграл 1-го и 2-го рода.
- •14. Числовые ряды, положительные числовые ряды, сумма ряда, необходимое условие сходимости ряда, основные теоремы о числовых рядах.
- •15. Признаки сходимости Даламбера, Коши, интегральный признак сходимости, признак сравнения, теорема о гармоничности ряда.
- •16. Знакопеременные(знакочередующиеся) ряды. Теорема Лейбница. Абсолютная и условная сходимость числового ряда.
- •17. Функциональные последовательности и ряды. Область сходимости функционального ряда. Равномерная сходимость, признак равномерной сходимости.
- •18. Степенные ряды, теорема Абеля.
- •19. Интегрирование и дифференцирование функциональных рядов.
- •20. Ряд Тейлора и ряд Маклорена.
- •28. Обыкновенное диф.Уравнение первого порядка. Задача Коши.Существование и единственность решения задачи Коши.
- •29.Уравнения с разделяющимися переменными.Диф.Уравнения в полных дифференциалах.Интегрирующий множитель.
6. Экстремум функции. Выпуклость функции, точки перегиба.
Пусть
функция
 определена на
определена на точка
точка
 называетсяточкой
локального максимума (минимума)
функции
называетсяточкой
локального максимума (минимума)
функции
 если существует окрестность
если существует окрестность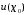 т.
т. такая что при всех
такая что при всех выполняется неравенство
выполняется неравенство (
( )
(1). Точка
)
(1). Точка называетсяточкой
строгого локального максимума (минимума)
если в (1) нестрогие неравенства можно
заменить строгими. Точка
называетсяточкой
строгого локального максимума (минимума)
если в (1) нестрогие неравенства можно
заменить строгими. Точка
 называетсяточкой
локального экстремума
если она является либо точкой локального
максимума (либо минимума).
называетсяточкой
локального экстремума
если она является либо точкой локального
максимума (либо минимума).
Пусть
функция
 определена на
определена на эта функция называетсявыпуклой
(вогнутой)
на
эта функция называетсявыпуклой
(вогнутой)
на
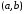 если касательная проведенная к графику
функции в любой его точке лежит выше
(ниже) графика. Функция выпуклая, если
если касательная проведенная к графику
функции в любой его точке лежит выше
(ниже) графика. Функция выпуклая, если выполняется неравенство
выполняется неравенство .
Функция вогнутая, если
.
Функция вогнутая, если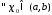 выполняется неравенство
выполняется неравенство .
.
Пусть
функция
 определена в некоторой окрестности
определена в некоторой окрестности точки
точки и имеет производную
и имеет производную т.
т. называетсяточкой
перегиба если
касательная к графику функции в т.
называетсяточкой
перегиба если
касательная к графику функции в т.
 относительно графиков функции изменяется
при переходе через
относительно графиков функции изменяется
при переходе через .
.
7. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица неопределенных интегралов.
Пусть
функция
 определена на
определена на тогда функция
тогда функция называетсяпервообразной
для функции
называетсяпервообразной
для функции
 если:
если:
1)
 непрерывна на
непрерывна на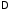 ;
;
2)
во внутренних точках промежутка
 функция
функция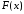 дифференцируема и удовлетворяет
равенству
дифференцируема и удовлетворяет
равенству .
.
Неопределенным
интегралом
от функции
 заданной на некотором промежутке
заданной на некотором промежутке называется совокупность всех ее
первообразных. Обозначается
называется совокупность всех ее
первообразных. Обозначается .
.
Свойства интеграла
1)
Производная от интеграла = подинтегральной
функции

2)
 ,
где
,
где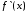 производная функции
производная функции
3) Линейность интеграла: интеграл суммы = сумме интегралов и const можно
выносить
за знак интеграла
 и
и
Таблица неопределенных интегралов
15.


16.
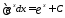
17.

18.

19.

20.

8. Интегрирование при помощи переменной и по частям.
Теорема
1 (правило замены переменной в неопределенном
интеграле):
пусть функция
 определена на промежутке
определена на промежутке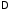 и имеет первообразную на этом промежутке
т. е. существует интеграл
и имеет первообразную на этом промежутке
т. е. существует интеграл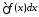 .
Пусть функция
.
Пусть функция определенная на промежутке
определенная на промежутке непрерывна на этом промежутке и имеет
производную
непрерывна на этом промежутке и имеет
производную в его внутренних точках, кроме того,
предположим, что
в его внутренних точках, кроме того,
предположим, что для любого
для любого тогда функция
тогда функция имеет первообразную на
имеет первообразную на и при этом
и при этом .
Данная формула означает, что для
нахождения интеграла в ее левой части
нужно найти интеграл (первообразную)
от функции
.
Данная формула означает, что для
нахождения интеграла в ее левой части
нужно найти интеграл (первообразную)
от функции и затем подставить вместоx
его значение
и затем подставить вместоx
его значение
 .
.
Доказательство:
Пусть
 - первообразная для функции
- первообразная для функции т. е.
т. е. рассмотрим функцию
рассмотрим функцию - непрерывна на
- непрерывна на как композиция непрерывных функций
как композиция непрерывных функций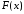 и
и во внутренних точках
во внутренних точках функция
функция имеет производную, которая вычисляется
по правилу дифференцирования сложной
функции т. е.
имеет производную, которая вычисляется
по правилу дифференцирования сложной
функции т. е. следовательно функция
следовательно функция есть первообразная для функции
есть первообразная для функции т. е. для подинтегральной функции в левой
части формулы
т. е. для подинтегральной функции в левой
части формулы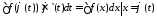 .
.
Теорема
2 (интегрирование по частям):
пусть функции
 и
и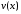 имеют производные на промежутке
имеют производные на промежутке тогда
тогда
 (формула
интегрирования по частям).
(формула
интегрирования по частям).
Доказательство:
Используя правило дифференцирования произведения

 интегрируя
это равенство получаем
интегрируя
это равенство получаем
 по определению интеграла следовательно
получаем
по определению интеграла следовательно
получаем
 .
.
9. Определенный интеграл. Формула Ньютона-Лейбница. Условие интегрирования функции.
Разбиением
отрезка
 называется конечный набор точек
называется конечный набор точек
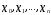 таких что
таких что .
Обозначается
.
Обозначается – разбиение т.
– разбиение т.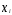 отрезка
отрезка .Мелкостью
разбиения
.Мелкостью
разбиения
 называется число
называется число
 – наибольшее из длин отрезков разбиения.
Пусть на
– наибольшее из длин отрезков разбиения.
Пусть на задана функция
задана функция пусть
пусть – некоторое разбиение, выберем внутри
каждого отрезка т.
– некоторое разбиение, выберем внутри
каждого отрезка т.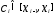 и составим сумму
и составим сумму .
Данная сумма называетсяинтегральной
суммой
функции
.
Данная сумма называетсяинтегральной
суммой
функции
 для разбиения
для разбиения и выбранных точек
и выбранных точек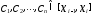 .
Обозначается
.
Обозначается или
или .
ЧислоI
называют пределом
интегральных сумм
.
ЧислоI
называют пределом
интегральных сумм
 если для любой последовательности
разбиений
если для любой последовательности
разбиений
 отрезка
отрезка такой что
такой что и при любом выбореn.
и при любом выбореn.
 соответствующая
разбиению
соответствующая
разбиению соответствует последовательность
интегральных сумм
соответствует последовательность
интегральных сумм сходится к числуI
т. е.
сходится к числуI
т. е.
 .
Функция
.
Функция определенная на отрезке
определенная на отрезке называетсяинтегрируемой
по Риману
если существует предел интегральных
сумм
называетсяинтегрируемой
по Риману
если существует предел интегральных
сумм
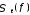 при
при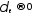 .
Этот предел называется определенным
интегралом (Римана) функции
.
Этот предел называется определенным
интегралом (Римана) функции по отрезку
по отрезку и обозначается
и обозначается .
. где
где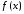 – подинтегральная функция,a
и b
– нижний и верхний пределы интегрирования.
– подинтегральная функция,a
и b
– нижний и верхний пределы интегрирования.
Формула Ньютона-Лейбница


Необходимое
условие интегрируемости:
если функция
 интегрируема на отрезке
интегрируема на отрезке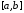 ,
то она ограничена на этом отрезке
,
то она ограничена на этом отрезке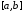 .
.
