
- •Математический анализ
- •1. Отображение множеств (функции). Область определения функции. Монотонные функции. Четные и нечетные функции. Периодические функции.
- •2. Предел последовательности. Предел суммы, разности, произведения. Предел функции на бесконечность, предел функции в точке. Замечательные пределы.
- •3. Непрерывность функции. 1-а и 2-а теоремы Больцано-Коши, 1-а и 2-а теоремы Вейерштраса.
- •5. Основные теоремы дифференциального исчисления Ферма, Ролля, Лагранжа и Коши.
- •6. Экстремум функции. Выпуклость функции, точки перегиба.
- •7. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица неопределенных интегралов.
- •8. Интегрирование при помощи переменной и по частям.
- •9. Определенный интеграл. Формула Ньютона-Лейбница. Условие интегрирования функции.
- •10. Площадь плоской фигуры, уравнение которой задано в явном виде, параметрическими уравнениями, в полярных координатах.
- •11. Длина дуги кривой, уравнение которой задано в явном виде, параметрическими уравнениями, уравнениями в полярных координатах.
- •12. Объем тела и объем тела вращения. Площадь поверхности вращения.
- •13. Несобственный интеграл 1-го и 2-го рода.
- •14. Числовые ряды, положительные числовые ряды, сумма ряда, необходимое условие сходимости ряда, основные теоремы о числовых рядах.
- •15. Признаки сходимости Даламбера, Коши, интегральный признак сходимости, признак сравнения, теорема о гармоничности ряда.
- •16. Знакопеременные(знакочередующиеся) ряды. Теорема Лейбница. Абсолютная и условная сходимость числового ряда.
- •17. Функциональные последовательности и ряды. Область сходимости функционального ряда. Равномерная сходимость, признак равномерной сходимости.
- •18. Степенные ряды, теорема Абеля.
- •19. Интегрирование и дифференцирование функциональных рядов.
- •20. Ряд Тейлора и ряд Маклорена.
- •28. Обыкновенное диф.Уравнение первого порядка. Задача Коши.Существование и единственность решения задачи Коши.
- •29.Уравнения с разделяющимися переменными.Диф.Уравнения в полных дифференциалах.Интегрирующий множитель.
3. Непрерывность функции. 1-а и 2-а теоремы Больцано-Коши, 1-а и 2-а теоремы Вейерштраса.
Определение2.
Функция
 называется непрерывной
в точке х0
если
называется непрерывной
в точке х0
если :
(2) Это определение предъявляет функции
:
(2) Это определение предъявляет функции следующие требования:1) функция
следующие требования:1) функция должна быть определена в точке х0
и некоторой ее окрестности.2)
Функция Функция
должна быть определена в точке х0
и некоторой ее окрестности.2)
Функция Функция
 должна
иметь в точке х0
предел.3) Этот предел
должен совпадать со значением функции
в точке х0
. Определение 2 означает, что для
непрерывности в точке х0
функции знаки lim и f функции
перестановочны, т.е.
должна
иметь в точке х0
предел.3) Этот предел
должен совпадать со значением функции
в точке х0
. Определение 2 означает, что для
непрерывности в точке х0
функции знаки lim и f функции
перестановочны, т.е.
 .
Предел функции равен функции от предела
аргумента. Если хотя бы одно из трех
требований предъявляемым к функции
.
Предел функции равен функции от предела
аргумента. Если хотя бы одно из трех
требований предъявляемым к функции в
определении 2 не выполняется, то говорят,
что функция
в
определении 2 не выполняется, то говорят,
что функция разрывна
в т. х0
или имеет в т. х0
разрыв; при этом предполагается, что
функция
разрывна
в т. х0
или имеет в т. х0
разрыв; при этом предполагается, что
функция
 определена в некоторой окрестности
определена в некоторой окрестности кроме быть может т. х0.
Тогда т. х0
- называется точкой разрыва функции
кроме быть может т. х0.
Тогда т. х0
- называется точкой разрыва функции . Определение 2 аналитически выражает
интуитивное представление о непрерывности
графика функции т.е. кривой
. Определение 2 аналитически выражает
интуитивное представление о непрерывности
графика функции т.е. кривой .
.
Первая
теорема Больцано-Коши:
Пусть
функция
 определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке
 и на концах этого промежутка принимает
значения разных знаков. Тогда между а
иb
необходимо найдется точка с, в которой
функция обращается в нуль:
и на концах этого промежутка принимает
значения разных знаков. Тогда между а
иb
необходимо найдется точка с, в которой
функция обращается в нуль:
 (a<c<b).
геометрический смысл: если непрерывная
кривая переходит с одной стороны оси х
на другую, то она пересекает эту ось.
(a<c<b).
геометрический смысл: если непрерывная
кривая переходит с одной стороны оси х
на другую, то она пересекает эту ось.
Доказательство.
(по методу деления промежутка). Для
определенности положим, что
 ,a
,a
 .
Разделим промежуток
.
Разделим промежуток пополам точкой
пополам точкой . может случиться, что функция
. может случиться, что функция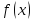 обратиться в нуль в этой точке, тогда
теорема доказана: можно положить
обратиться в нуль в этой точке, тогда
теорема доказана: можно положить .
пусть также
.
пусть также ,
тогда на концах одного из промежутков
,
тогда на концах одного из промежутков функция будет принимать значения разных
знаков(и притом отрицательное значение
на левом конце и положительное – на
правом). Обозначив этот промежуток через
функция будет принимать значения разных
знаков(и притом отрицательное значение
на левом конце и положительное – на
правом). Обозначив этот промежуток через ,
имеем
,
имеем .
Разделим пополам промежуток
.
Разделим пополам промежуток и
снова отбросим тот случай, когда
и
снова отбросим тот случай, когда обращается в нуль
обращается в нуль
В
середине
 этого промежутка, ибо тогда теорема
доказана. Обозначим через
этого промежутка, ибо тогда теорема
доказана. Обозначим через ту
из половин промежутка, для которой
ту
из половин промежутка, для которой 0.
0.
Продолжим
этот процесс построения промежутков.
При этом либо мы после конечного числа
шагов наткнемся в качестве точки деления
на точку, где функция обращается в нуль,
и док-во завершится, либо получим
бесконечную последовательность вложенных
один в другой промежутков. Тогда для
k-го промежутка
 ,
k∈N
будем иметь
,
k∈N
будем иметь
 0
(1), причем длина его, очевидно, равна
0
(1), причем длина его, очевидно, равна (2).
(2).
Построенная
последовательность промежутков
удовлетворяет условиям леммы о вложенных
промежутках, ибо, ввиду (2) , поэтому обе переменные
, поэтому обе переменные и
и стремятся к общему пределу
стремятся к общему пределу .,
который очевидно, принадлежит
.,
который очевидно, принадлежит .Покажем,
что именно эта точка удовлетворяет
требованию теоремы. Переходя к пределу
в неравенствах (1) и используя при этом
непрерывность функции (в точке х=с),
получим, что
.Покажем,
что именно эта точка удовлетворяет
требованию теоремы. Переходя к пределу
в неравенствах (1) и используя при этом
непрерывность функции (в точке х=с),
получим, что так
что действительно
так
что действительно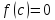 .
.
Вторая
теорема Больцано – Коши.
Пусть функция
 определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке и на концах этого промежутка принимает
не равные значения f(a)=A и f(b)=В. Тогда,
каково бы ни было число C, лежащее между
А и В, найдется такая точка c междуa
и b,
что f(c)=C.
и на концах этого промежутка принимает
не равные значения f(a)=A и f(b)=В. Тогда,
каково бы ни было число C, лежащее между
А и В, найдется такая точка c междуa
и b,
что f(c)=C.
Доказательство: Основано на первой теореме Больцано-Коши.
Будем
считать, например, А<B,
так что A<C<B.
рассмотрим на промежутке
 вспомогательную функцию φ(x)=f(x)−C она
непрерывна в промежутке и на концах его
имеет разные знаки:
вспомогательную функцию φ(x)=f(x)−C она
непрерывна в промежутке и на концах его
имеет разные знаки: (b)=f(b)−C=B−C>0,
:
(b)=f(b)−C=B−C>0,
: (a)=f(a)−C=A−C<0,
тогда по первой теореме между a и b
найдется точка с, такая что
(a)=f(a)−C=A−C<0,
тогда по первой теореме между a и b
найдется точка с, такая что
 (c)=0,
т.е. f(c)-C=0 или f(c)=C. ч.т.д.
(c)=0,
т.е. f(c)-C=0 или f(c)=C. ч.т.д.
Геометрический смысл этой теоремы: всякая прямая y=C, где B<C<A, пересечет график функции f по крайней мере в одной точке.
Замечание. Если f - непрерывна и непостоянна на I, то образом этого промежутка I при отображении f будет также промежуток (т.е. непрерывным образ f(I)промежутка I есть промежуток). В самом деле, по теореме из того, что B,A∈E(f)следует, что интервал (B;A)⊂E(f), т.е. E(f)⊂f(I)- промежуток.
Первая теорема Вейерштрасса.
Если
функция
 определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке ,
то она ограничена и знизу и сверху, т.е.
существуют такие постоянные и конечные
числаm
и М, что
,
то она ограничена и знизу и сверху, т.е.
существуют такие постоянные и конечные
числаm
и М, что
 при
при .
.
Доказательство:
методом от противного,допустим, что
функция при изменении х в промежутке
при изменении х в промежутке
 оказывается неограниченной, скажем,
сверху. В таком случае для каждого
натурального числа n
найдется в промежутке
оказывается неограниченной, скажем,
сверху. В таком случае для каждого
натурального числа n
найдется в промежутке
 такое значение х=хn,
что
f(xn)
такое значение х=хn,
что
f(xn) n.(3)
n.(3)
По
лемме Больцано-Вейерштрасса, из
последовательности
 ,сходящуюся
к конечному пределу:
,сходящуюся
к конечному пределу:
 (при
(при )
, причем,очевидно,
)
, причем,очевидно,
 .
Вследствие непрерывности функции в
точке
.
Вследствие непрерывности функции в
точке ,
тогда должно быть и
,
тогда должно быть и ,
а это не возможно, так как из (3) следует,
что
,
а это не возможно, так как из (3) следует,
что .
Получено противоречие. Теорема доказана.
.
Получено противоречие. Теорема доказана.
Вторая теорема Вейерштрасса.
Если
функция
 определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке ,
то она достигает в этом промежутке своих
точных верхней и нижней границ. Иными
словами, в промежутке
,
то она достигает в этом промежутке своих
точных верхней и нижней границ. Иными
словами, в промежутке найдутся такие точки х0
и х1,
что значения
найдутся такие точки х0
и х1,
что значения
 и
и ,
будут, соответственно, наибольшим и
наименьшим из всех значений функции
,
будут, соответственно, наибольшим и
наименьшим из всех значений функции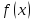 .
.
Доказательство.
Положим
 ,
по предыдущей теореме, это – число
конечное. Предположим, что всегда
,
по предыдущей теореме, это – число
конечное. Предположим, что всегда <M,
т.е., что граница М не достигается. В
таком случае, можно рассмотреть
вспомогательную функцию
<M,
т.е., что граница М не достигается. В
таком случае, можно рассмотреть
вспомогательную функцию
 . Так как , по предположению, знаменатель
здесь в нуль не обращается, то эта функция
будет непрерывна, а следовательно (по
предыдущей теореме), ограничена:
. Так как , по предположению, знаменатель
здесь в нуль не обращается, то эта функция
будет непрерывна, а следовательно (по
предыдущей теореме), ограничена: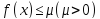 .
Но тогда легко получить, что тогда
.
Но тогда легко получить, что тогда <M-
<M- ,
т.е. числоM-
,
т.е. числоM- ,
меньше чем М, оказывается верхней
границей для значений функции
,
меньше чем М, оказывается верхней
границей для значений функции ,
чего быть не может, ибо М есть точная
верхняя граница этих значений. Полученное
противоречие доказывает теорему: в
промежутке
,
чего быть не может, ибо М есть точная
верхняя граница этих значений. Полученное
противоречие доказывает теорему: в
промежутке найдется такое значение
найдется такое значение
 , что
, что
 будет наибольшим из всех значений
будет наибольшим из всех значений .
Аналогично может быть доказано утверждение
и относительно наименьшего значения.
.
Аналогично может быть доказано утверждение
и относительно наименьшего значения.
4. Производная функции, геометрический и механический смысл производной. Таблица производной. Производные сложных функций. Правила дифференцирования. Дифференциал функции. Уравнение касательной к графику функции.
Пусть
функция
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
 ,
эта функция имеет производную в точке
,
эта функция имеет производную в точке если существует предел
если существует предел при этом значение предела
при этом значение предела называетсяпроизводной
функцией
называетсяпроизводной
функцией
 в точке
в точке .
.
 приращение
аргумента
приращение
аргумента
 приращение
функции
приращение
функции
Геометрический и механический смысл производной
Прямая
 является касательной к графику функции
является касательной к графику функции в точке
в точке если выполнено условие
если выполнено условие ,
т.е. если
,
т.е. если имеет вид:
имеет вид: .
Касательная к графику функцииy
существует тогда и только тогда когда
функция y
дифференцируема в точке
.
Касательная к графику функцииy
существует тогда и только тогда когда
функция y
дифференцируема в точке
 .
Касательной оказывается прямая,
проходящая через точку
.
Касательной оказывается прямая,
проходящая через точку с угловым коэффициентом
с угловым коэффициентом .
.
 .
Коэффициент растяжения в точке x
равен
.
Коэффициент растяжения в точке x
равен
 .
.
Производная характеризует скорость изменения функции при изменении аргумента; в частности: производная времени является мерой скорости изменений, используемой по отношению к различным физическим величинам. Например, мгновенная скорость v неравномерного прямолинейного движения является производной от функции, выражающей зависимость пройденного пути S от времени t.
Производная сложной функции:
Пусть:
1) функция
 имеет в некоторой точке х0
производную
имеет в некоторой точке х0
производную
 ,
2) функция
,
2) функция имеет в соответствующей точке
имеет в соответствующей точке производную
производную
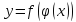 в упомянутой точке х0
также будет
иметь производную, равную произведению
производных функций
в упомянутой точке х0
также будет
иметь производную, равную произведению
производных функций
 и
и :
: или короче
или короче .
.
Правила дифференцирования:
 ,
2)
,
2)
 ,
3)
,
3) ,
4)
,
4) все они доказываются из соответствующих
правил для производных:
все они доказываются из соответствующих
правил для производных:



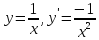






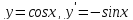


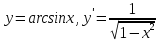



Пусть
имеем функцию
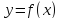 ,
определенную в некотором промежутке Х
и непрерывную в рассматриваемой точкех0.
Тогда приращение
,
определенную в некотором промежутке Х
и непрерывную в рассматриваемой точкех0.
Тогда приращение
 аргумента отвечает приращение
аргумента отвечает приращение
 ;
бесконечно малое вместе с
;
бесконечно малое вместе с .
Большую важность имеет вопрос, существует
ли для
.
Большую важность имеет вопрос, существует
ли для такая линейная относительно
такая линейная относительно бесконечно малая
бесконечно малая ,
что их разность оказывается, по сравнению
с
,
что их разность оказывается, по сравнению
с ,
бесконечно малой высшего порядка:
,
бесконечно малой высшего порядка: .(1).
При
.(1).
При наличие равенства (1) показывает, что
бесконечно малая
наличие равенства (1) показывает, что
бесконечно малая эквивалентна бесконечно малой
эквивалентна бесконечно малой и значит, служит для последней ее главной
частью, если за основную бесконечно
малую взята
и значит, служит для последней ее главной
частью, если за основную бесконечно
малую взята .
Если равенство (1) выполняется, то функция
.
Если равенство (1) выполняется, то функция называется дифференцируемой (при данном
значении х=
называется дифференцируемой (при данном
значении х= ),
само же выражение
),
само же выражение называется дифференциалом функции и
обозначается символом
называется дифференциалом функции и
обозначается символом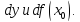 Т.О. дифференциал функции характеризуется
2 свойствами: (а) он представляет линейную
однородную функцию от приращения
Т.О. дифференциал функции характеризуется
2 свойствами: (а) он представляет линейную
однородную функцию от приращения аргумента и (б) разнится от приращения
функции на величину, которая при
аргумента и (б) разнится от приращения
функции на величину, которая при является бесконечно малой, порядка
высшего, чем
является бесконечно малой, порядка
высшего, чем .
.






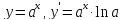











Пусть
функция
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки эта функция называется дифференцируемой
в точке
эта функция называется дифференцируемой
в точке если ее можно представить в виде
если ее можно представить в виде
 ,
где A
– некоторое число.
,
где A
– некоторое число.
Пусть
функция
 определена на интервале
определена на интервале эта функция имеет производную на
интервале
эта функция имеет производную на
интервале если она имеет производную в каждой
точке
если она имеет производную в каждой
точке т. е. эта функция дифференцируема в
каждой точке
т. е. эта функция дифференцируема в
каждой точке в этом случае также говорят, что функция
в этом случае также говорят, что функция дифференцируема
на интервале
дифференцируема
на интервале .
.
Уравнение касательной к графику функции

