
- •Математический анализ
- •1. Отображение множеств (функции). Область определения функции. Монотонные функции. Четные и нечетные функции. Периодические функции.
- •2. Предел последовательности. Предел суммы, разности, произведения. Предел функции на бесконечность, предел функции в точке. Замечательные пределы.
- •3. Непрерывность функции. 1-а и 2-а теоремы Больцано-Коши, 1-а и 2-а теоремы Вейерштраса.
- •5. Основные теоремы дифференциального исчисления Ферма, Ролля, Лагранжа и Коши.
- •6. Экстремум функции. Выпуклость функции, точки перегиба.
- •7. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица неопределенных интегралов.
- •8. Интегрирование при помощи переменной и по частям.
- •9. Определенный интеграл. Формула Ньютона-Лейбница. Условие интегрирования функции.
- •10. Площадь плоской фигуры, уравнение которой задано в явном виде, параметрическими уравнениями, в полярных координатах.
- •11. Длина дуги кривой, уравнение которой задано в явном виде, параметрическими уравнениями, уравнениями в полярных координатах.
- •12. Объем тела и объем тела вращения. Площадь поверхности вращения.
- •13. Несобственный интеграл 1-го и 2-го рода.
- •14. Числовые ряды, положительные числовые ряды, сумма ряда, необходимое условие сходимости ряда, основные теоремы о числовых рядах.
- •15. Признаки сходимости Даламбера, Коши, интегральный признак сходимости, признак сравнения, теорема о гармоничности ряда.
- •16. Знакопеременные(знакочередующиеся) ряды. Теорема Лейбница. Абсолютная и условная сходимость числового ряда.
- •17. Функциональные последовательности и ряды. Область сходимости функционального ряда. Равномерная сходимость, признак равномерной сходимости.
- •18. Степенные ряды, теорема Абеля.
- •19. Интегрирование и дифференцирование функциональных рядов.
- •20. Ряд Тейлора и ряд Маклорена.
- •28. Обыкновенное диф.Уравнение первого порядка. Задача Коши.Существование и единственность решения задачи Коши.
- •29.Уравнения с разделяющимися переменными.Диф.Уравнения в полных дифференциалах.Интегрирующий множитель.
Математический анализ
1. Отображение множеств (функции). Область определения функции. Монотонные функции. Четные и нечетные функции. Периодические функции.
Пусть
XиYпроизвольные множества, тогдафункциейдействующей изXвYназывается некоторое правило, согласно
которому каждому элементуx Xставится в соответствие единственный
элементy
Xставится в соответствие единственный
элементy Y.
Функция, действующая изXвYобозначается
Y.
Функция, действующая изXвYобозначается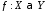 .
.
Множество
Xназываютобластью
определения функции (
(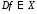 ).
).
Пусть
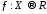 некоторая числовая функция
некоторая числовая функция ,
тогда
,
тогда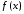 называетсявозрастающей (убывающей),
если
называетсявозрастающей (убывающей),
если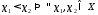
 (
(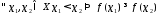 ).
).
Функция, которая возрастает или убывает называется монотонной.
Функция
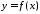 называетсячетной (нечетной), если
для любого значенияxиз
области определения значение (-x)
также принадлежит области определения
и выполняется равенство
называетсячетной (нечетной), если
для любого значенияxиз
области определения значение (-x)
также принадлежит области определения
и выполняется равенство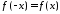 (
( ).
).
Функция
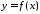 называетсяпериодическойс периодом
называетсяпериодическойс периодом ,
если для любогоxиз области
определения функции числа
,
если для любогоxиз области
определения функции числа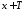 и
и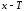 также принадлежат области определения
и выполняется условие
также принадлежат области определения
и выполняется условие
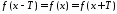 .
.
2. Предел последовательности. Предел суммы, разности, произведения. Предел функции на бесконечность, предел функции в точке. Замечательные пределы.
Упорядочение
значений переменной
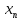 по возрастанию их номеров, приведшее к
рассмотрению последовательности
по возрастанию их номеров, приведшее к
рассмотрению последовательности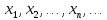 этих значений,
облегчает понимание «процесса»
приближения переменной
этих значений,
облегчает понимание «процесса»
приближения переменной
 - при безграничном возрастанииn
– к ее пределу а. Число a
называется пределом переменной
- при безграничном возрастанииn
– к ее пределу а. Число a
называется пределом переменной
 ,
если для каждого положительного числа
,
если для каждого положительного числа ,
сколько бы мало оно ни было, существует
такой номерN,
что все значения
,
сколько бы мало оно ни было, существует
такой номерN,
что все значения
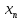 ,
у которых номерn>N,
удовлетворяет неравенству
,
у которых номерn>N,
удовлетворяет неравенству
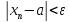 (1).
(1).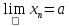 ,
переменная стремиться к а:
,
переменная стремиться к а: .
Число а называют также пределом
последовательности
.
Число а называют также пределом
последовательности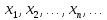 , и говорят, что эта
последовательность сходится к а. (1)
равносильно:
, и говорят, что эта
последовательность сходится к а. (1)
равносильно:
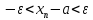 или
или .
Открытый промежуток (
.
Открытый промежуток (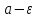 ,
, ),
с центром в точке а, принято называть
окрестностью этой точки. Таким образом,
какую бы малую окрестность точки а ни
взять, все значения
),
с центром в точке а, принято называть
окрестностью этой точки. Таким образом,
какую бы малую окрестность точки а ни
взять, все значения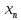 ,
начиная с некоторого из них, должны
попасть в эту окрестность.Число
,
начиная с некоторого из них, должны
попасть в эту окрестность.Число называютпределом числовой
последовательности
называютпределом числовой
последовательности если для любого
если для любого найдется
найдется такое что при всех
такое что при всех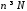 выполняется неравенство
выполняется неравенство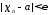 .
Обозначается
.
Обозначается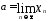 .
.
Пусть
 ,
, две последовательности такие, что
две последовательности такие, что тогда
тогда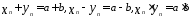 .
Эти свойства можно записать
.
Эти свойства можно записать
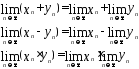
Таким образом, предел суммы= сумме пределов,предел разности= разности пределов,предел произведения= произведению пределов.
Определение
(по Коши):Пусть функция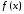 определена на множестве
определена на множестве ,
где
,
где числоAназывают пределом
функции
числоAназывают пределом
функции при
при ,
если для любой окрестности
,
если для любой окрестности найдется число
найдется число такое что при всехxудовлетворяет неравенству
такое что при всехxудовлетворяет неравенству и выполняется включение
и выполняется включение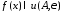 .
.
Определение
(по Гейне):ЧислоA–
предел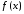 при
при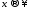 ,
если для любого
,
если для любого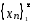 такой что
такой что последовательность
последовательность сходится кA.
сходится кA.
Определение
(по Коши):Пусть функция определена в некоторой проколотой
окрестности
определена в некоторой проколотой
окрестности числоAназывают пределом
функции
числоAназывают пределом
функции при
при ,
если
,
если найдется положительное число
найдется положительное число такое что при всех
такое что при всех и удовлетворяющему неравенству
и удовлетворяющему неравенству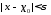 выполняется неравенство
выполняется неравенство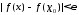 .
.
Определение
(по Гейне):Пусть функция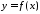 определена в некоторой проколотой
окрестности
определена в некоторой проколотой
окрестности точки
точки ,
числоAназывают пределом
функции
,
числоAназывают пределом
функции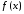 при
при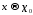 ,
если для любой последовательности
,
если для любой последовательности такой что
такой что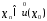 и
и последовательность
последовательность сходится к числуA.
сходится к числуA.
Первый замечательный предел
Теорема
1: при

 ,
,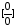
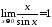

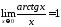
Второй замечательный предел
Теорема
2: существует конечный предел
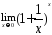 .
Этот предел называет число
.
Этот предел называет число ,
т. е.
,
т. е.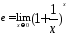 .
Число
.
Число играет важную роль в математике. Это
число иррациональное.
играет важную роль в математике. Это
число иррациональное.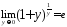
Третий замечательный предел

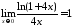

Четвертый
замечательный предел

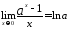
Пятый
замечательный предел


