§38. Культура запису розв'язань задач

: Текстові задачі в початковому курсі математики розв'язують окремими діями ^без пояснення, з поясненням, за письмовим планом); способом складання виразу (без пояснення, з поясненням, готовий вираз); деякі прості задачі — способом складання рівнянь.

Розгляньмо вимоги до оформлення письмового розв'язання задач.

1-й клас. У першому класі початкової школи розв'язують тільки прості задачі. Запис розв'язання виконують у вигляді рівності, розміщеної посередині рядка.

Першокласникам іноді пропонують проілюструвати задачу малюнком. Для позначення предметів, про які йдеться в задачі, здебільшого викорис­товують кружечки, палички, трикутники, квадрати. У цьому разі розв'язання записують під малюнком (мал. 118).

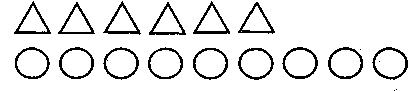
Мал. 118

2-й клас. Ще в процесі розв'язування простих задач учням варто показати, як коротко записувати задачу в один рядок, табличним способом і у вигляді структурного запису. Вони не роблять короткий запис задачі у зошиті, а розглядають його на дошці. З опорою на цей запис повторюють задачу, але розв'язання виконують так само, як і в першому класі.

Після ознайомлення зі складеною задачею діти вчаться записувати коротко задачі в зошиті, але виконують такі завдання за зразком і під керівництвом учителя. На цей час запроваджується найменування предметів у відповідях дій. Назви предметів записують однією буквою з крапкою в дужках після числа: 13 — 6 = 7 (в.). У відповідях до задачі назви предметів пишуть повністю (7 вагонів). Слова, що починаються на голосний, скорочують, як правило, до наступного голосного (яблуко — ябл., ялина — ял.). У короткому записі задач назви предметних дій (купили, продали, відрізали тощо) краще записувати повним словом. Якщо предмети, про які йдеться в задачі, відрізняються певною ознакою, то в короткому записі слід вказувати як ознаку, так і предмет. Для схематичного запису задач на знаходження суми запроваджується також фігурна дужка.

Для одного і того самого виду задач необов'язково застосовувати єдину форму короткого запису. Краще, щоб учні звикали до думки, що коротко задачу можна записувати по-різному. •■ • ■

Методика викладання математики в початкових класах

233

Задача. У бідоні міститься 9 л молока, а в каструлі — на 6л менше. Скільки літрів молока у бідоні і в каструлі разом ?

Б.-9 л.

К. — на 6 л менше.

Разом — ?

Б.-9 л.

К. — на 6 л менше.

Розв'язання задач записують окремими діями без пояснення (пояснення дають в усній формі).

1) 9 - 6 = 3 (л);

2) 9 + 3 = 12 (л). Відповідь. 12 л молока.

Застосування короткого позначення предметів може бути для дітей нелегкою справою. Тому вчитель здебільшого сам повідомляє дітям, як коротко позначити предмети у схематичному записі задачі чи в її розв'язанні.

У кінці вивчення нумерації в межах 100 ознайомлюють учнів із розв'я­занням задач складанням виразу.

У подальшій роботі вчитель сам визначає, як оформити запис розв'язання: окремими діями чи складанням виразу. Зрозуміло, що всі складені задачі з буквеними даними розв'язують складанням виразу.

Розв'язання однієї і тієї самої задачі й окремими діями, і складанням виразу практикують в окремих випадках як вид творчої роботи.

У другому півріччі запроваджують короткий запис відповіді задачі. Записують здобуте число і найменування.

У підручниках для 2-4 класів запроваджується така форма завдання, як розв'язування задач за даним планом. У 2 класі учні такий план взагалі не переписують у зошит, а учні 3 і 4 класів переписують його у зошит лише на вимогу вчителя.

3-й клас. У 3 класі учні вчаться записувати повну відповідь і короткі пояснення розв'язання. Із записом повної відповіді ознайомлюють дітей на початку навчального року. Записувати повну відповідь до кожної задачі не варто. На уроках треба практикувати як короткі, так і повні відповіді, а в домашніх і контрольних роботах повну відповідь записувати обов'язково.

Навчати коротко записувати пояснення ходу розв'язування задачі можна почати в середині першого семестру.

Задача. На 45 грн. купили набори олівців ціною по 5 грн. Стільки ж купили наборів фарб ціною по 8 грн. Скільки гривень заплатили за набори фарб?

Назва	Ціна	Кількість	Вартість
Набори олівців	5 грн.	Однакова	45 грн.
Набори фарб	8 грн.		?

1) 45 : 5 = 9 (ол.) наборів олівців;

2) 8 • 9 = 72 (к.) — заплатили за набори фарб. 232

РозділХІ. Навчання учнів розв 'язувати текстові задачі

Залежно від конкретної ситуації і поставленої мети відповіді можна давати як до початку розв'язування задачі, так і після нього. Якщо учень припустився помилки, то бажано дати йому час поміркувати, щоб він самостійно чи з допомогою вчителя знайшов правильний план розв'язування.