
IND_ZAD_1DID
.docИНДИВИДУАЛЬНОЕ ЗАДАНИЕ ПО ВЫСШЕЙ МАТЕМАТИКЕ
для студентов 1 курса специальности «Документоведение и информационная деятельность»
дневной формы обучения
-
В задачах 1-10 даны координаты вершин пирамиды
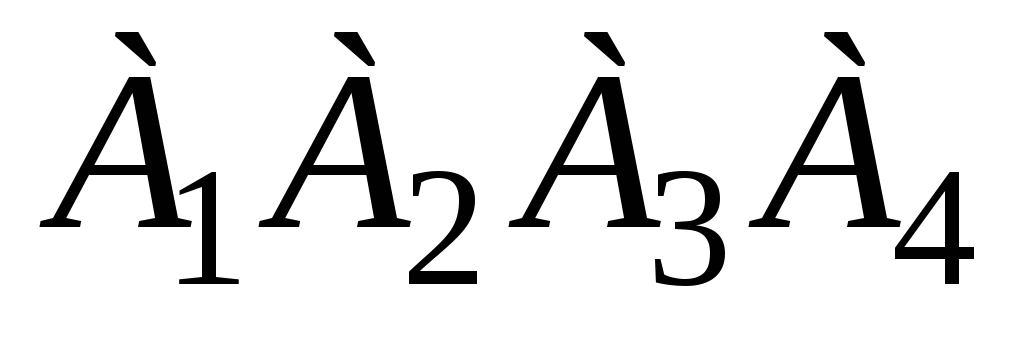 .
Средствами векторной алгебры найти:
.
Средствами векторной алгебры найти:-
угол между ребрами
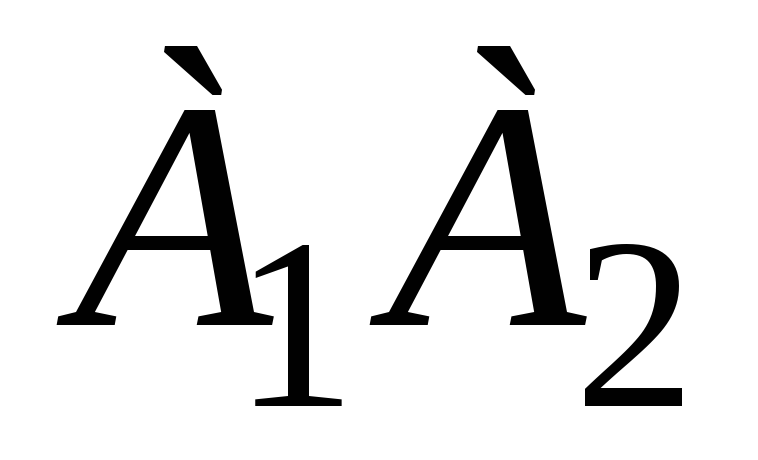 и
и
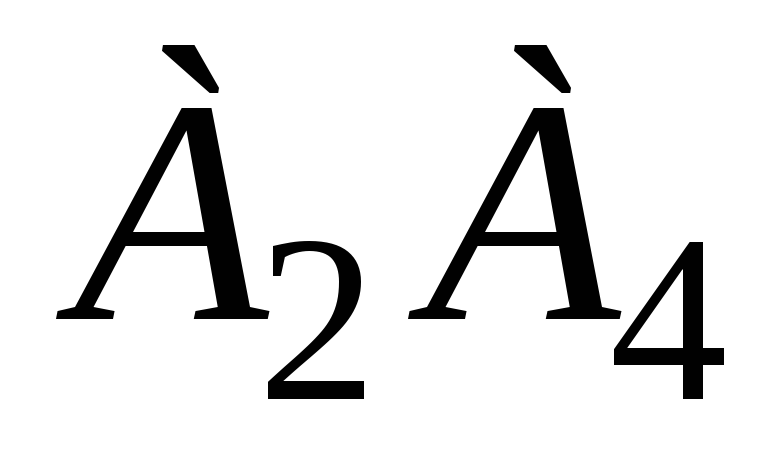 ;
; -
площадь грани
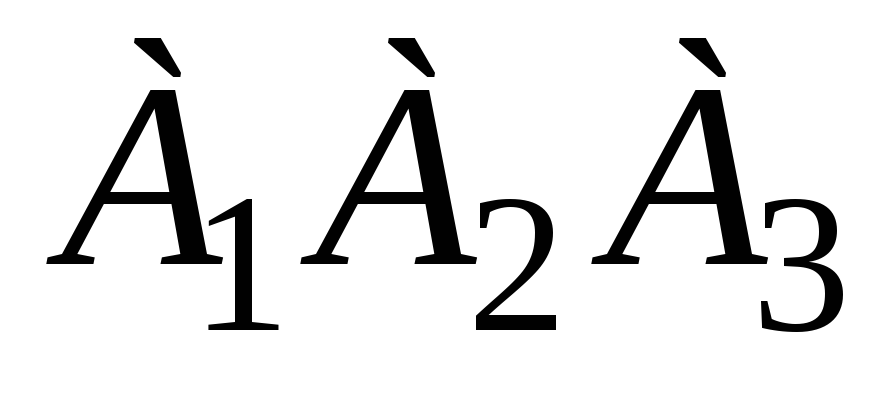 ;
; -
проекцию вектора
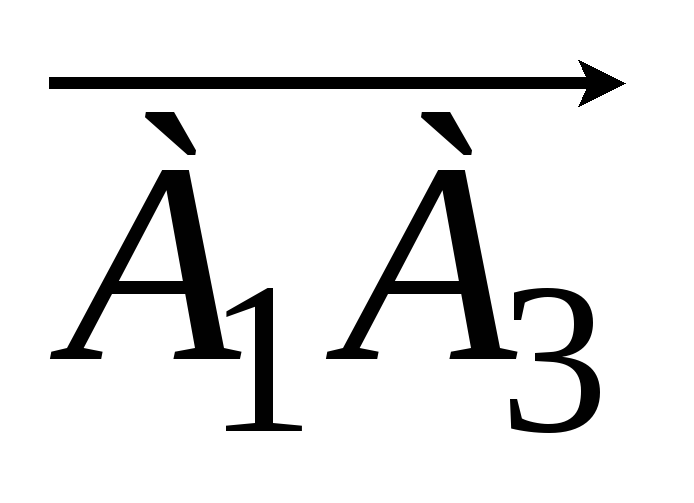 на вектор
на вектор
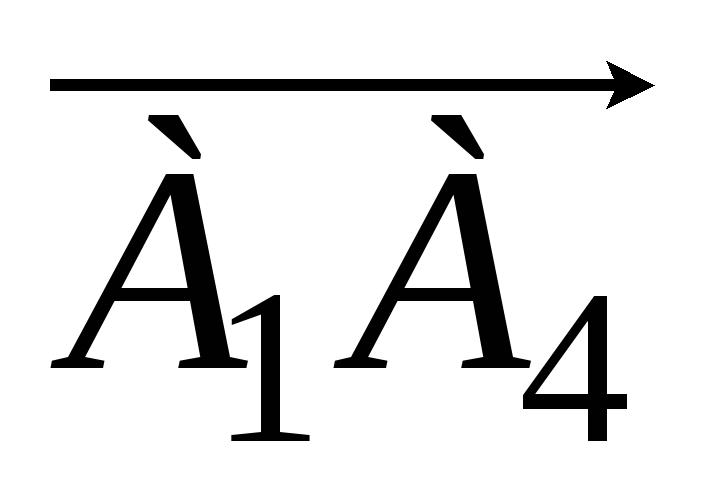 ;
; -
объем пирамиды.
-
1.
![]() .
.
2.
![]()
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
-
В задачах 11-20 даны координаты точек
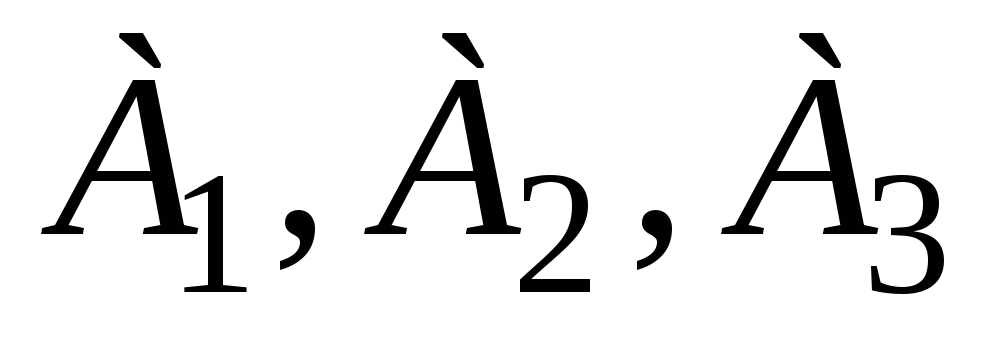 .
Найти:
.
Найти:-
уравнение прямой, проходящей через точки
 и
и
 ,
, -
угол между прямыми
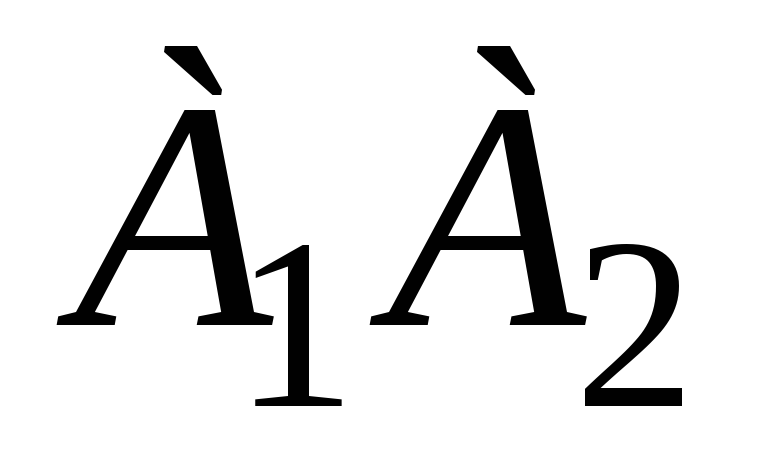 и
и
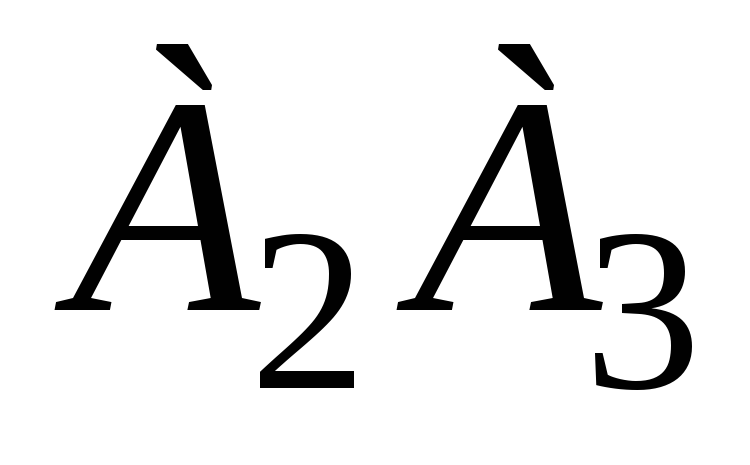 ,
, -
расстояние от точки
 до прямой
до прямой
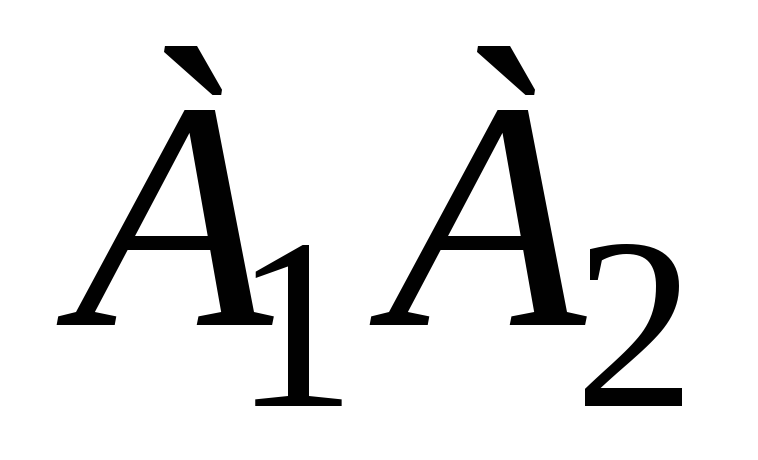 ,
, -
уравнение прямой, проходящей через точку
 параллельно
прямой
параллельно
прямой
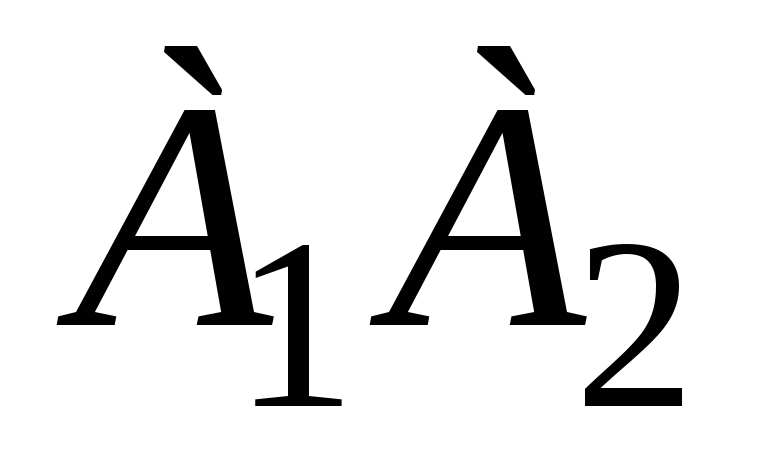 ,
, -
уравнение прямой, проходящей через точку
 перпендикулярно
прямой
перпендикулярно
прямой
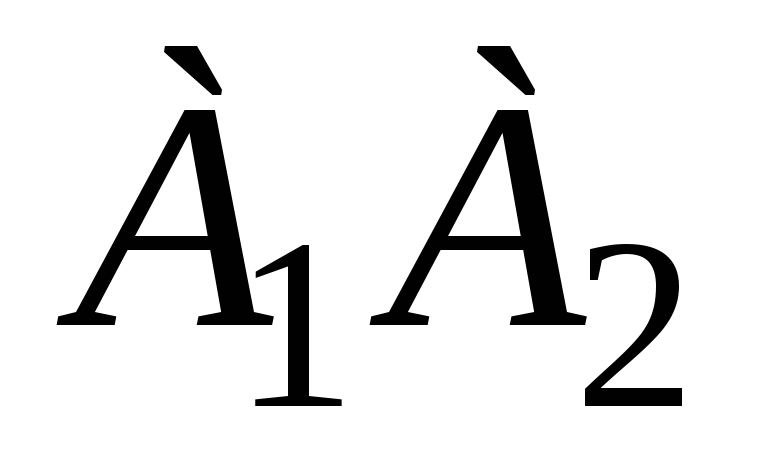 .
.
-
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
-
В задачах 21-30 найти все точки пересечения трех следующих плоскостей:
-
плоскости
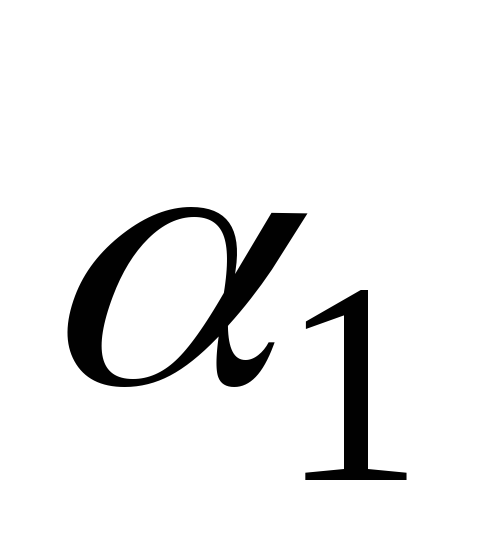 ,
заданной общим уравнением
,
заданной общим уравнением
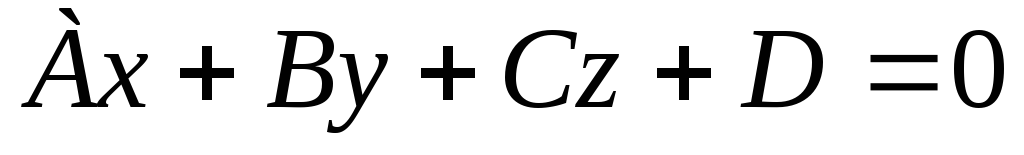 ;
; -
плоскости
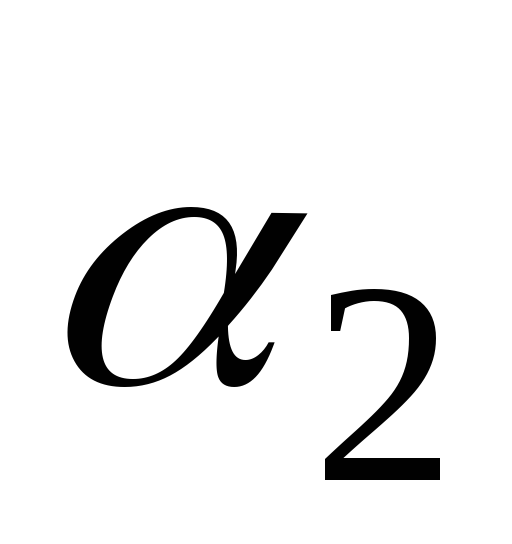 ,
проходящей через точки
,
проходящей через точки
 ,
, -
плоскости
 ,
проходящей через точку
,
проходящей через точку
 перпендикулярно вектору
перпендикулярно вектору
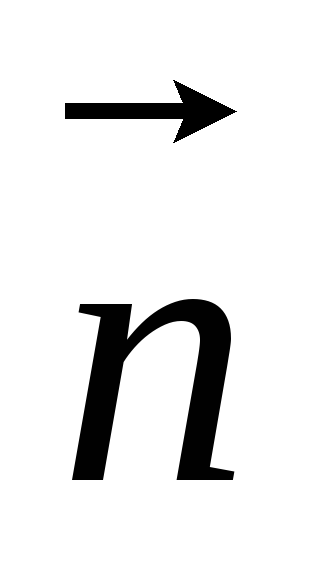 .
.
-
|
№ |
А |
B |
C |
D |
|
|
|
|
|
|
21. |
2 |
-3 |
1 |
2 |
(-5;0;0) |
(0;-1;0) |
(6;1;1) |
(0;-4;0) |
|
|
22. |
2 |
-4 |
3 |
1 |
(-1;0;1) |
(3;0;0) |
(0;-1;1) |
(0;-2;0) |
|
|
23. |
3 |
2 |
-1 |
0 |
(0;0;0) |
(-1;1;1) |
(-3;0;2) |
(1;1;2) |
|
|
24. |
2 |
-1 |
1 |
2 |
(0;0;-1) |
(0;-1;0) |
(2;-2;2) |
(0;0;1) |
|
|
25. |
1 |
2 |
3 |
5 |
(1;1;0) |
(1;0;1) |
(0;-2;1) |
(6;0;0) |
|
|
26. |
1 |
1 |
1 |
1 |
(0;3;0) |
(-1;1;2) |
(5;1;-4) |
(1;-1;0) |
|
|
27. |
1 |
1 |
-2 |
2 |
(0;1;1) |
(1;1;0) |
(-3;0;0) |
(0;0;2) |
|
|
28. |
3 |
-1 |
2 |
9 |
(0;0;0) |
(1;1;1) |
(3;-2;0) |
(1;1;-2) |
|
|
29. |
1 |
1 |
-1 |
7 |
(-10;0;0) |
(-1;3;0) |
(-2;0;-4) |
(-1;0;-2) |
|
|
30. |
2 |
-1 |
3 |
9 |
(-2;0;-1) |
(0;1;1) |
(2;2;0) |
(1;0;1) |
|
-
В задачах 31-40 дана точка
 ,
плоскость и прямая. Найти:
,
плоскость и прямая. Найти:-
точку
 ,
симметричную точке
,
симметричную точке
 относительно данной плоскости,
относительно данной плоскости, -
точку
 ,
симметричную точке
,
симметричную точке
 относительно данной прямой,
относительно данной прямой, -
угол между данными прямой и плоскостью,
-
точки пересечения прямой, параллельной заданной и проходящей через точку
 ,
с координатными плоскостями.
,
с координатными плоскостями.
-
31.
![]() .
.
32.
![]() .
.
33.
![]() .
.
34.
![]() .
.
35.
![]() .
.
36.
![]() .
.
37.
![]() .
.
38.
![]() .
.
39.
![]() .
.
40.
![]() .
.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИ. ИНДИВИДУАЛЬНОГО ЗАДАНИЯ.
Задача 1. Пусть пирамида задана
вершинами![]() .
Средствами векторной алгебры найти:
.
Средствами векторной алгебры найти:
-
угол между ребрами
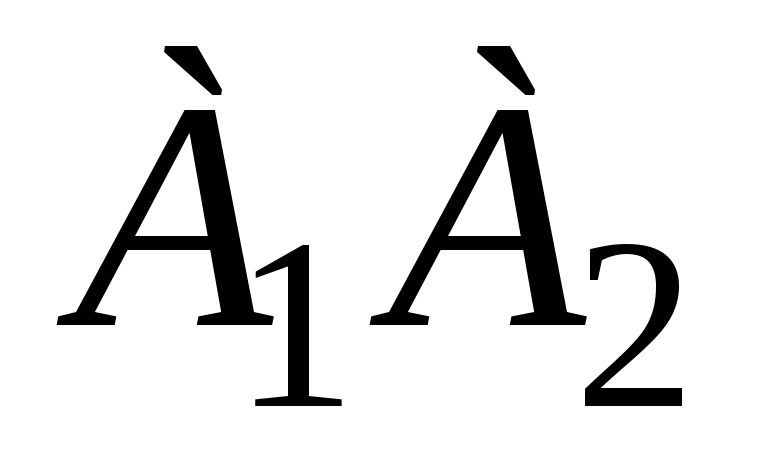 и
и
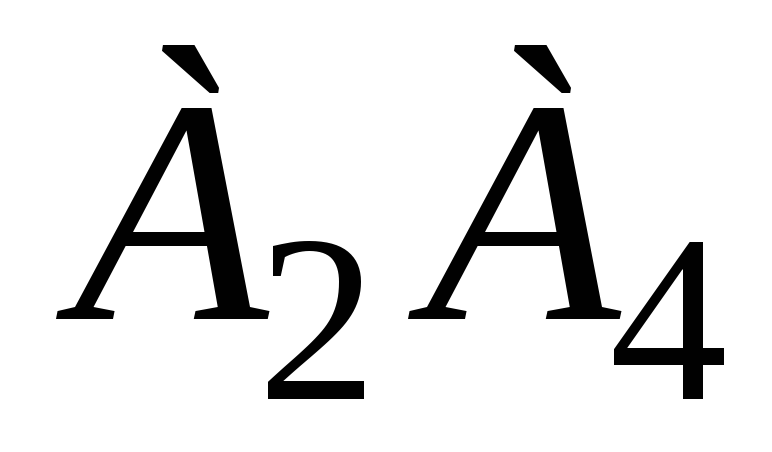 ;
; -
площадь грани
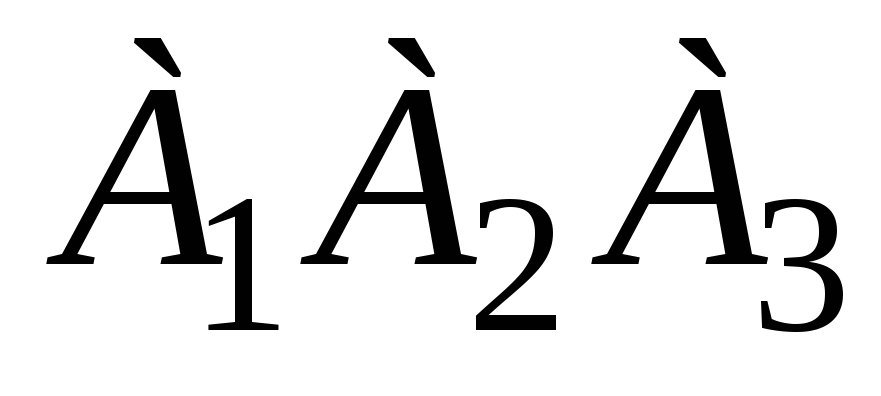 ;
; -
проекцию вектора
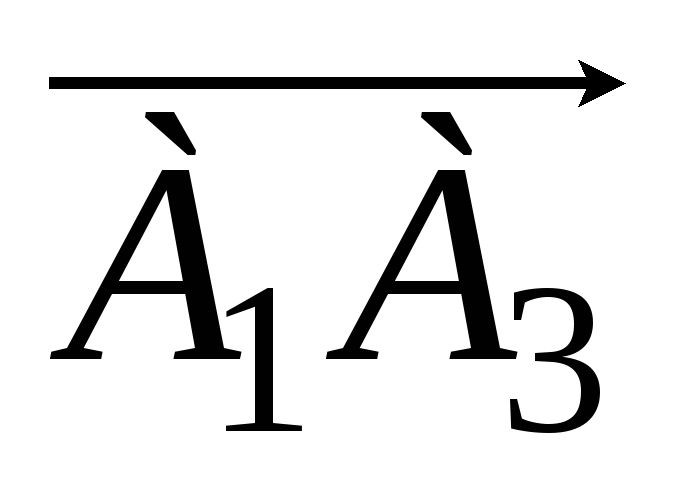 на вектор
на вектор
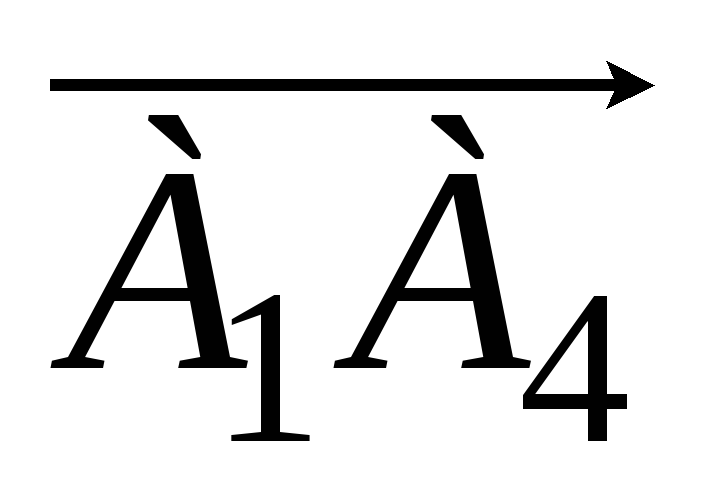 ;
; -
объем пирамиды.
Решение.
-
Угол между ребрами
 и
и
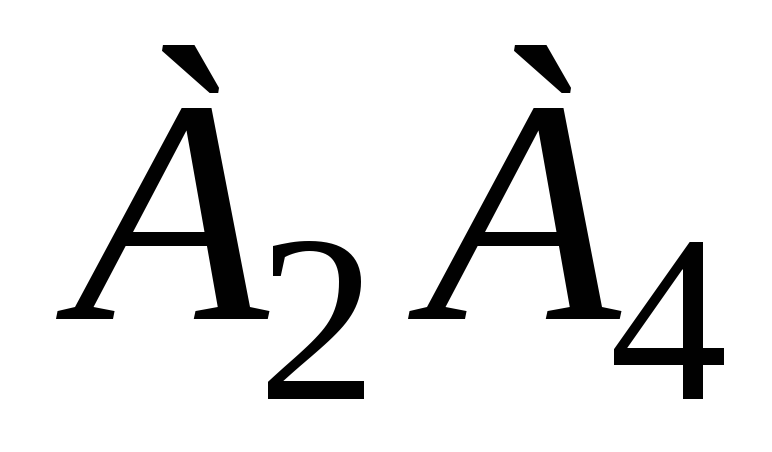 равен углу между векторами
равен углу между векторами
 и
и
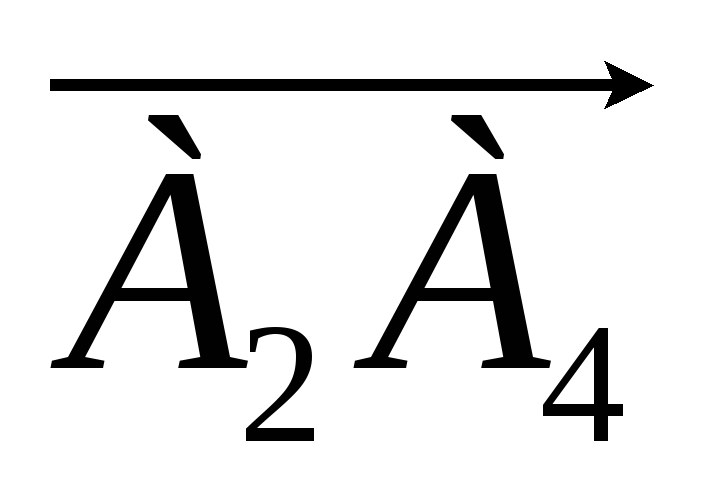 .
.
Так как
![]() ,
то
,
то
![]() Поэтому:
Поэтому:
![]() ,
так что
,
так что
![]()
![]() .
.
-
Грань
 есть треугольник, площадь которого
равна половине площади параллелограмм,
построенного на векторах
есть треугольник, площадь которого
равна половине площади параллелограмм,
построенного на векторах
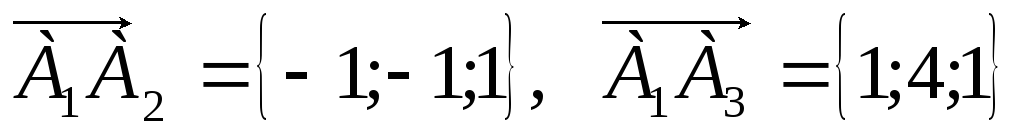 .
Найдем сначала векторное произведение
.
Найдем сначала векторное произведение
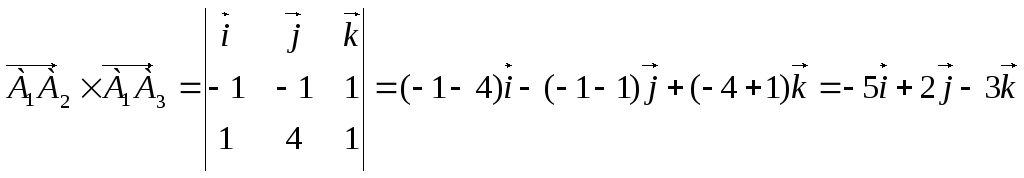 .
.
Тогда
![]() .
.
3). Проекция вектора
![]() на вектор
на вектор
![]() находится по формуле
находится по формуле
![]() .
В нашем случае
.
В нашем случае
![]() .
.
![]()
![]()
![]()
Поэтому
![]() .
.
4). Пирамида
![]() построена на векторах
построена на векторах
![]() .
В п.2 найдено векторное произведение
.
В п.2 найдено векторное произведение
![]() .
Тогда
.
Тогда
![]() .
Так как объем пирамиды
.
Так как объем пирамиды
![]() есть
есть![]() часть объема параллелепипеда, построенного
на векторах
часть объема параллелепипеда, построенного
на векторах
![]() то
то
![]()
Задача 2. На плоскости заданы
точки
![]() .
Найти:
.
Найти:
-
уравнение прямой, проходящей через точки
 и
и
 ,
, -
угол между прямыми
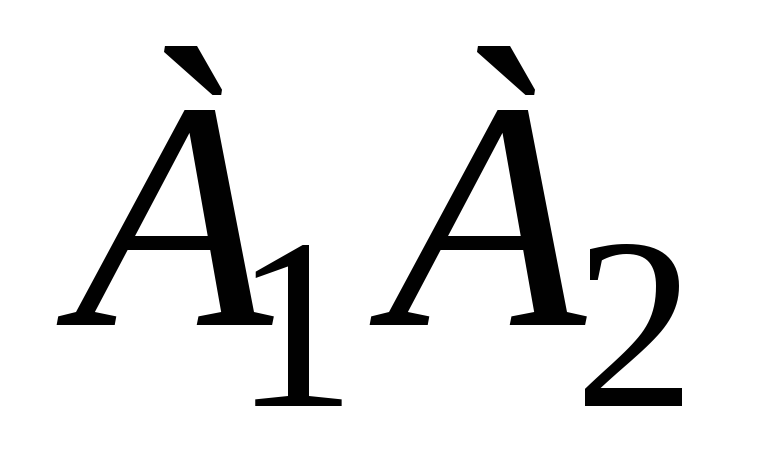 и
и
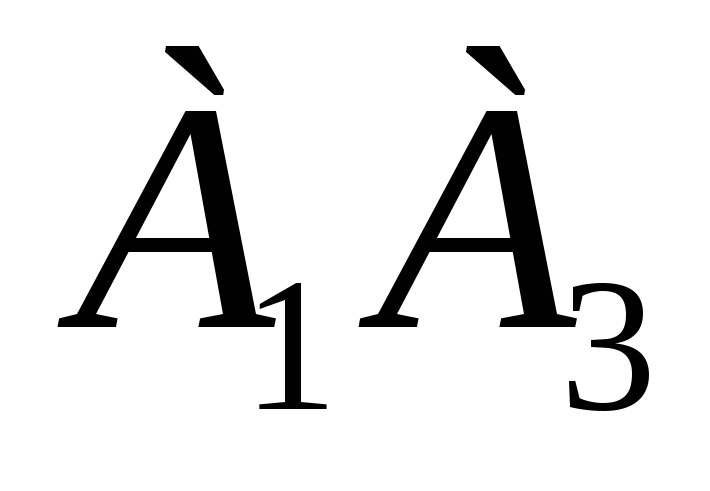 ,
, -
расстояние от точки
 до прямой
до прямой
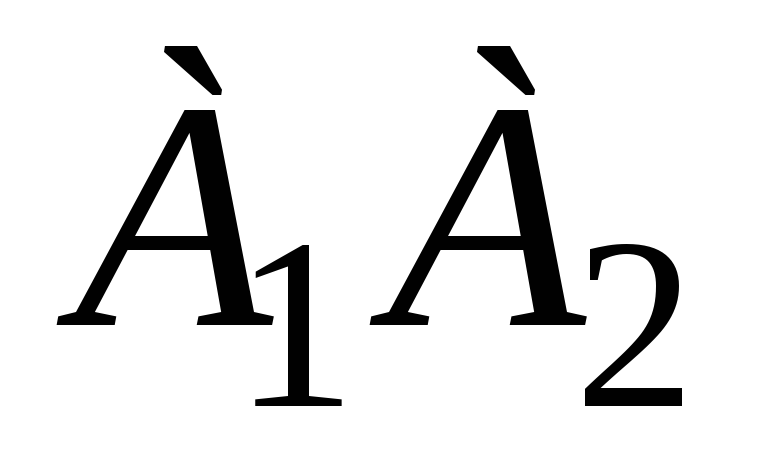 ,
, -
уравнение прямой, проходящей через точку
 параллельно
прямой
параллельно
прямой
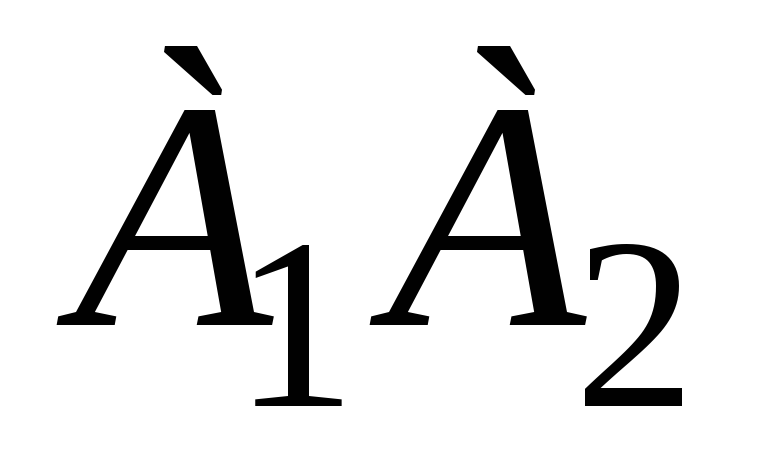 ,
, -
уравнение прямой, проходящей через точку
 перпендикулярно
прямой
перпендикулярно
прямой
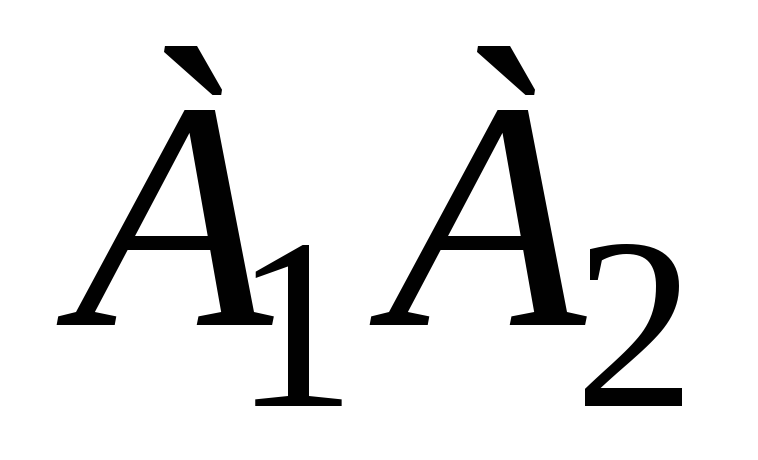 .
.
Решение.
-
Уравнение прямой, проходящей через точки
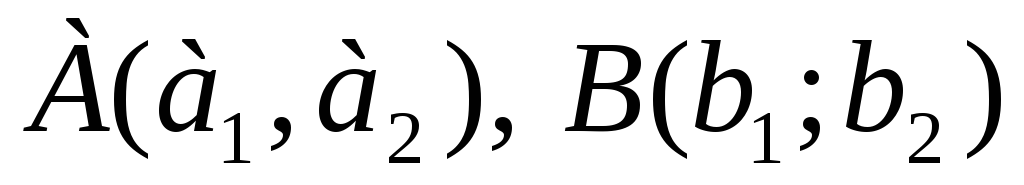 ,
имеет вид
,
имеет вид
![]() .
В нашем случае :
.
В нашем случае :![]() ,
т.е.
,
т.е.
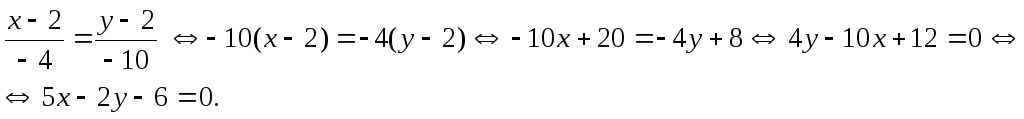
Это и есть уравнение прямой, проходящей
через точки
![]() и
и
![]() .
.
-
Угол между прямыми
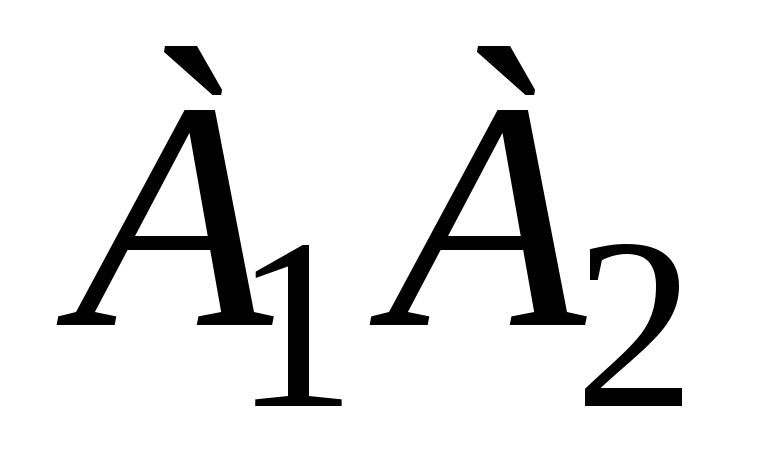 и
и
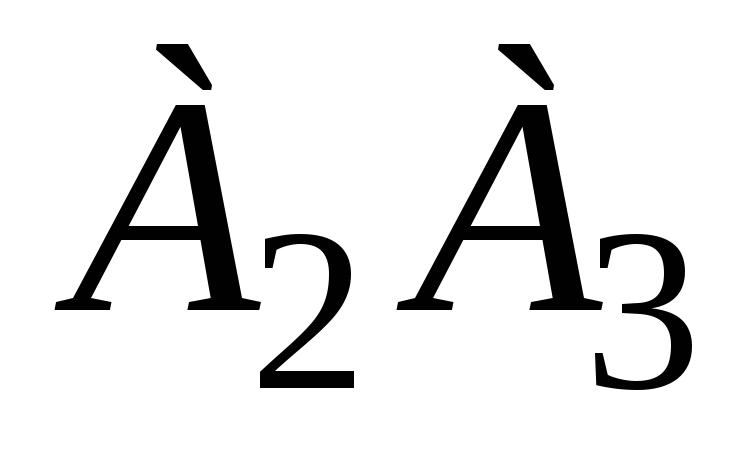 равен углу между векторами
равен углу между векторами
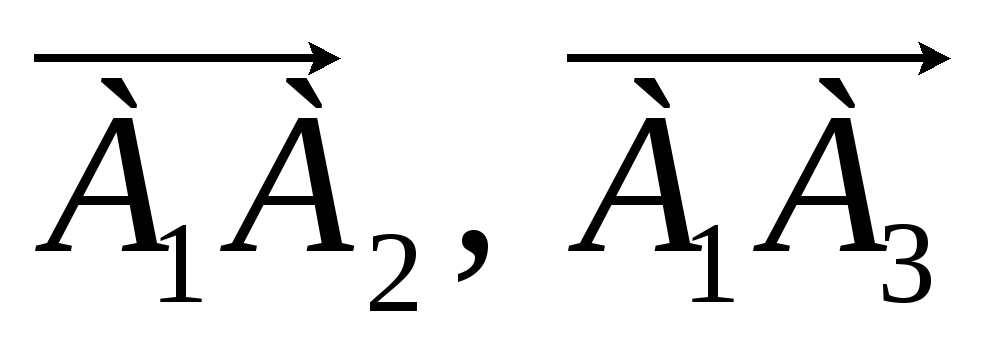 ,
который может быть найден из формулы
,
который может быть найден из формулы
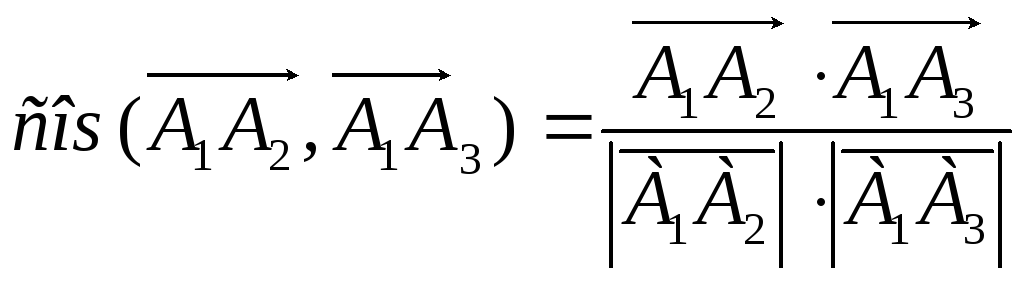 .
.
Так как
![]() ,
то
,
то
![]() .
.
Поэтому
![]() .
.
-
Расстояние
 от точки
от точки
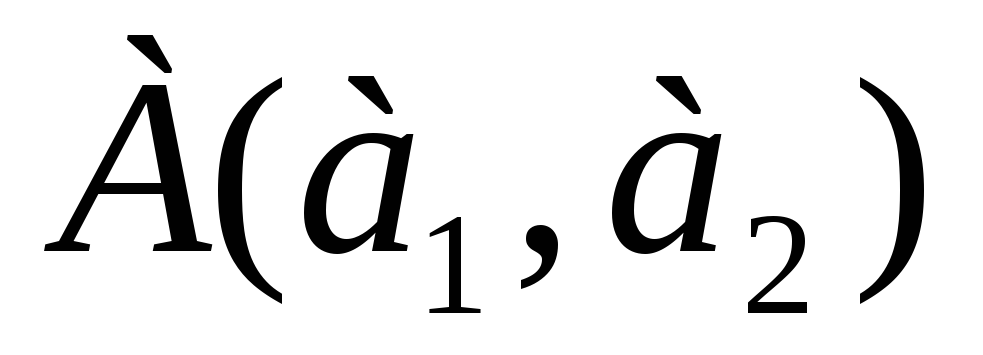 до прямой
до прямой
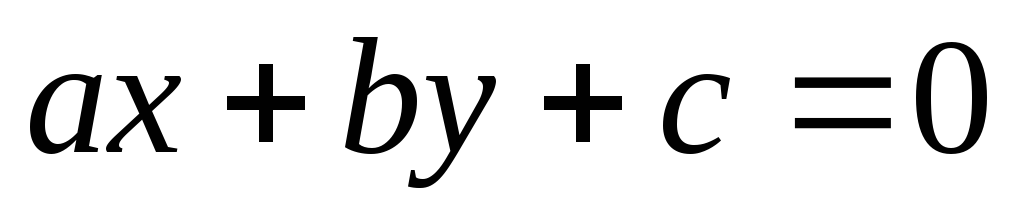 находится по формуле:
находится по формуле:
![]() .
В нашем случае нужно найти расстояние
от точки
.
В нашем случае нужно найти расстояние
от точки
![]() до прямой
до прямой
![]() ,
имеющей уравнение
,
имеющей уравнение
![]() Имеем:
Имеем:
![]() .
.
-
Запишем сначала уравнение прямой
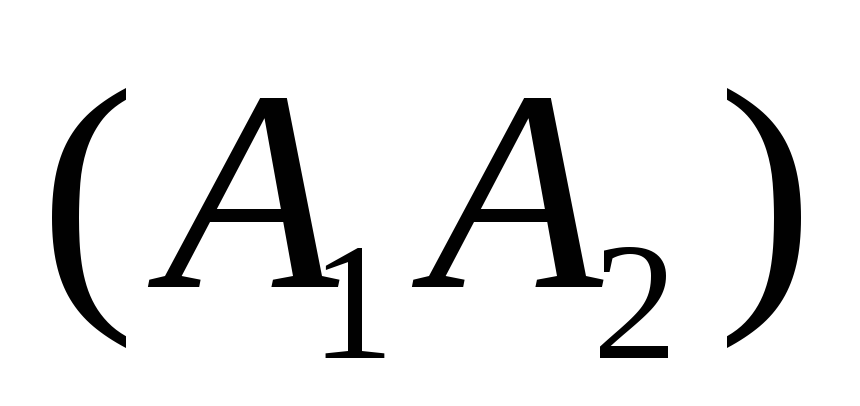 в виде
в виде
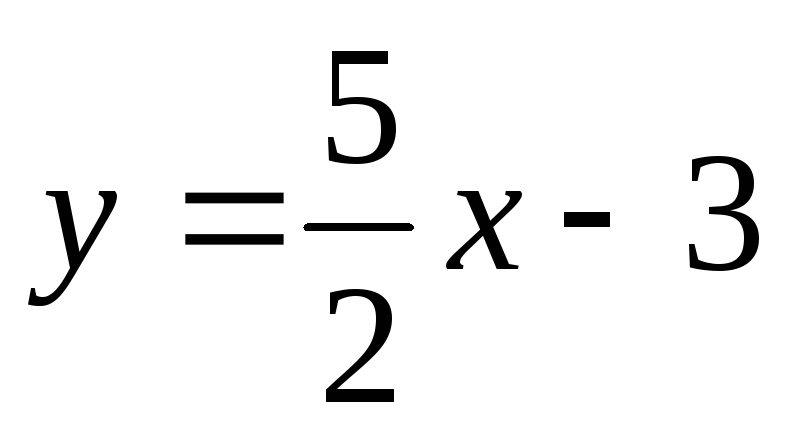 ,
из которого находим ее угловой коэффициент
,
из которого находим ее угловой коэффициент
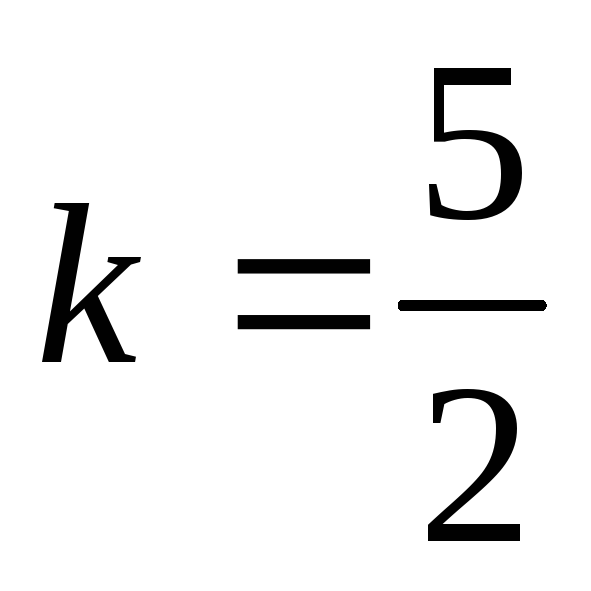 .
Так как прямая должна проходить через
точку
.
Так как прямая должна проходить через
точку
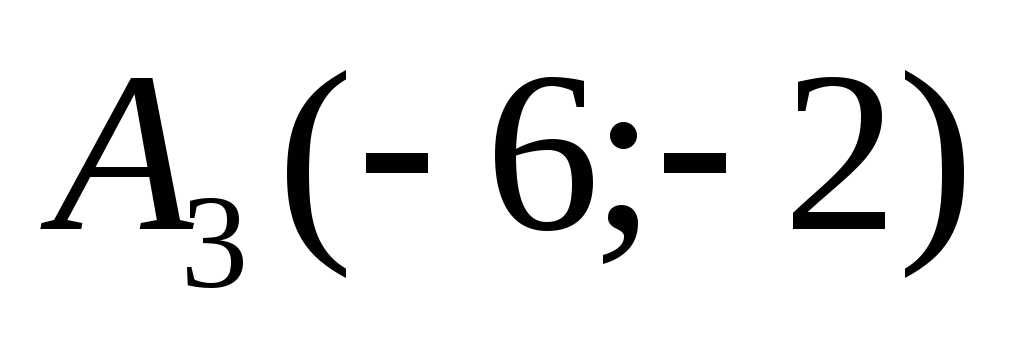 параллельно прямой
параллельно прямой
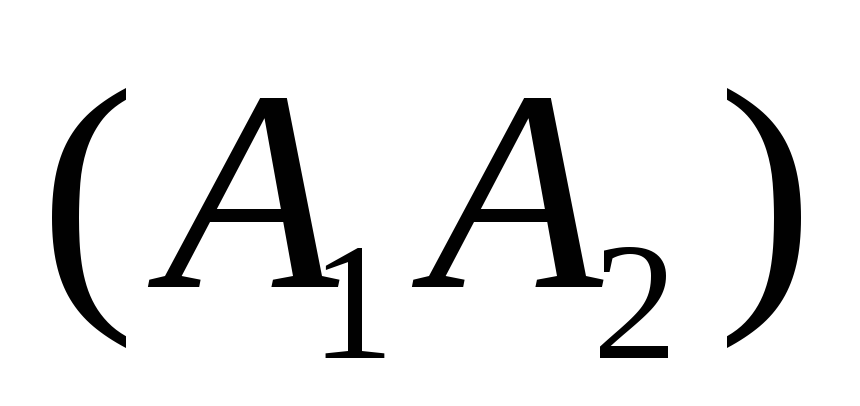 ,
то ее уравнение должно иметь вид:
,
то ее уравнение должно иметь вид:
![]() ,
т.е.
,
т.е.
![]() или
или
![]() - уравнение прямой, проходящей через
точку
- уравнение прямой, проходящей через
точку
![]() параллельно прямой
параллельно прямой
![]() .
.
-
Угловой коэффициент
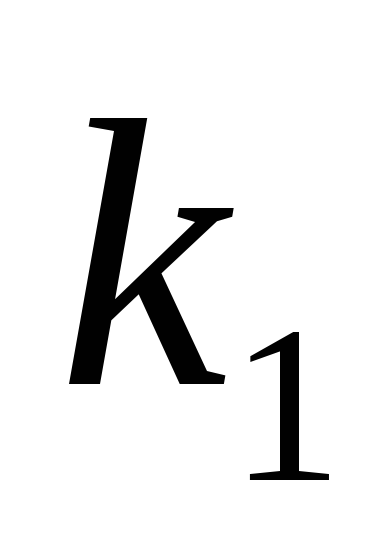 прямой, проходящей через точку
прямой, проходящей через точку
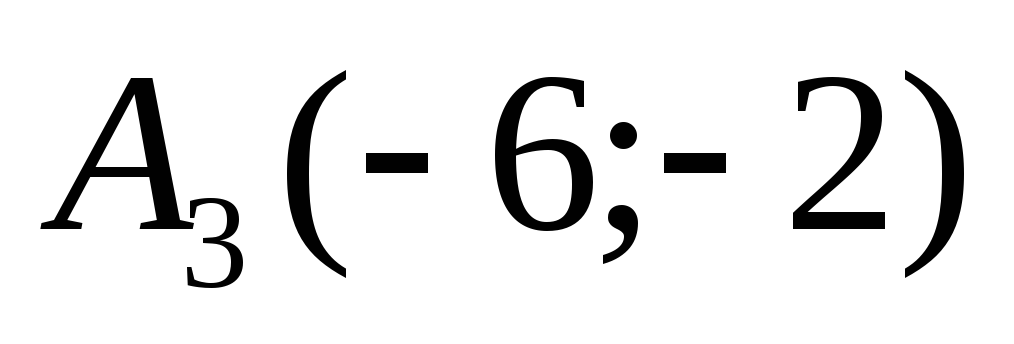 перпендикулярно прямой
перпендикулярно прямой
 ,
связан с угловым коэффициентом последней
соотношением
,
связан с угловым коэффициентом последней
соотношением
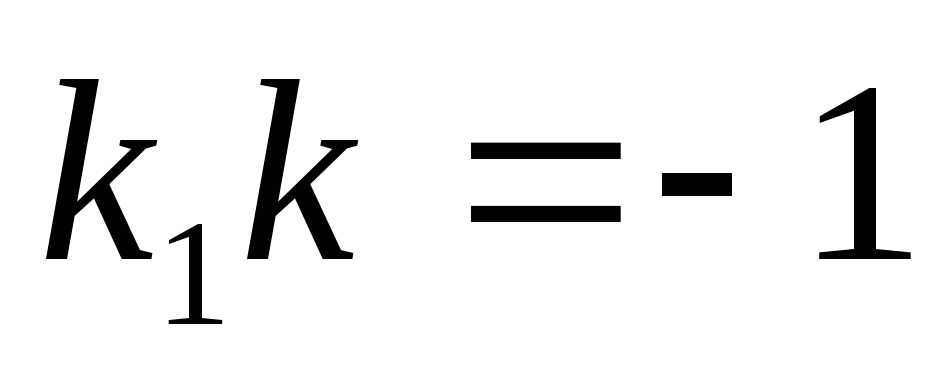 .
Отсюда
.
Отсюда
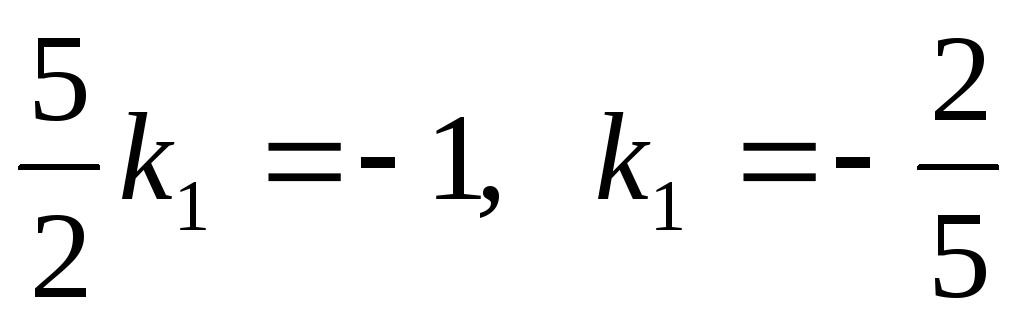 .
Поэтому
.
Поэтому
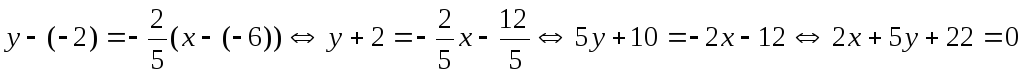 .
.
![]() - это уравнение прямой, проходящей через
точку
- это уравнение прямой, проходящей через
точку
![]() перпендикулярно прямой
перпендикулярно прямой
![]() .
.
Задача 3. Найти все точки пересечения трех следующих плоскостей:
-
плоскости
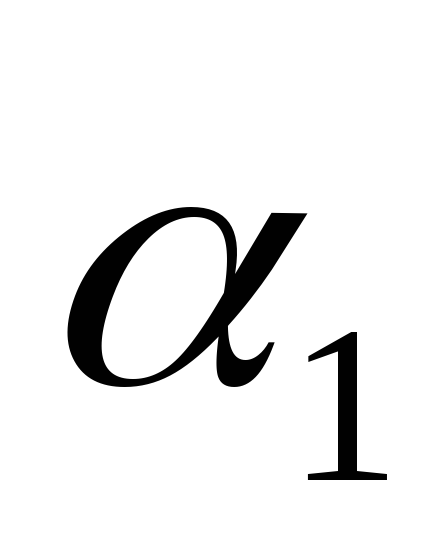 ,
заданной уравнением
,
заданной уравнением
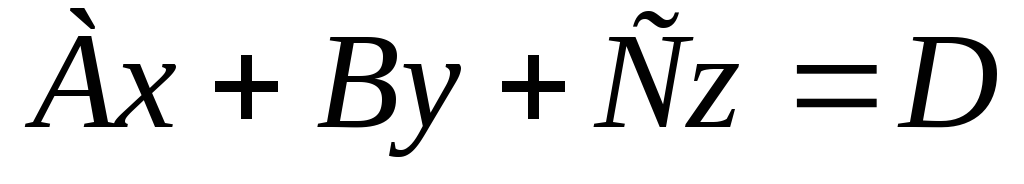 ;
; -
плоскости
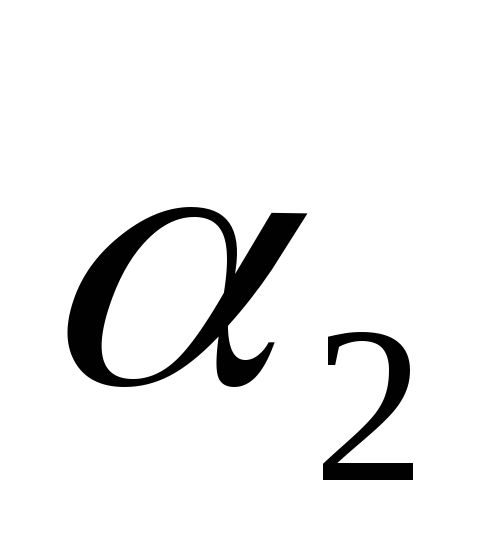 ,
проходящей через точки
,
проходящей через точки
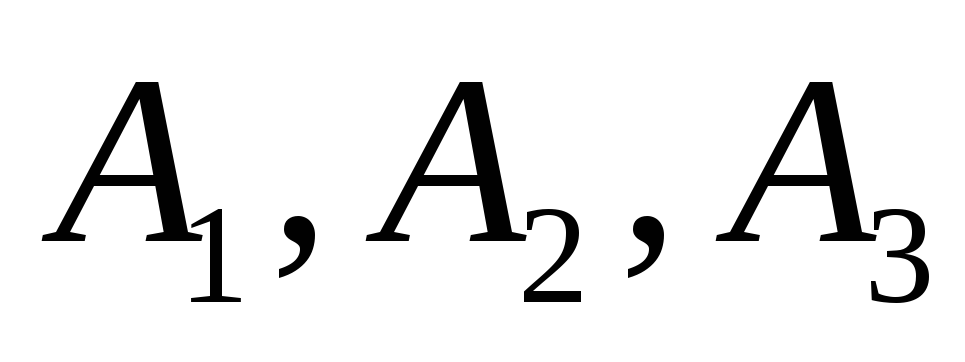 ;
; -
плоскости
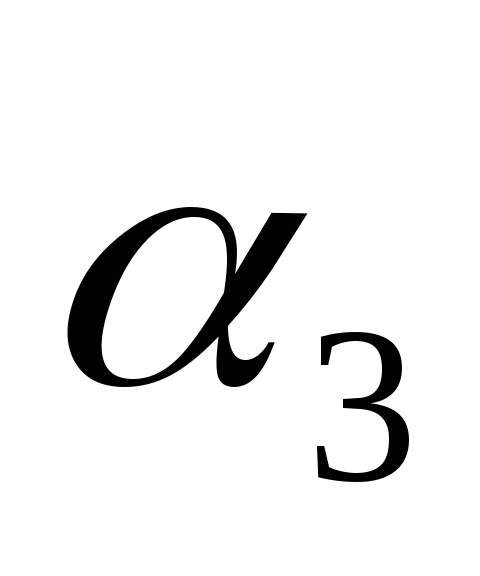 ,
проходящей через точку
,
проходящей через точку
 перпендикулярно вектору
перпендикулярно вектору
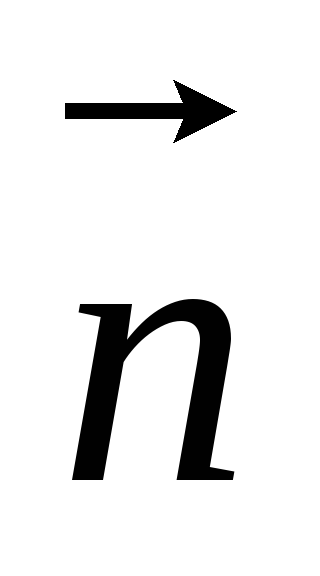 ,
если известно, что
,
если известно, что
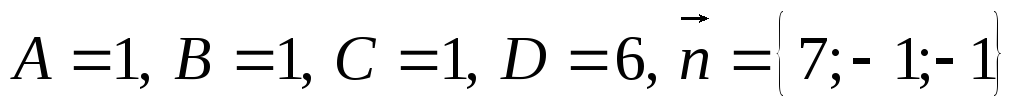
![]() .
.
Решение.
Плоскость
![]() определяется уравнением
определяется уравнением
![]() .
Для нахождения уравнения плоскости
.
Для нахождения уравнения плоскости
![]() воспользуемся тем фактом, что уравнение
плоскости, проходящей через точки
воспользуемся тем фактом, что уравнение
плоскости, проходящей через точки
![]()
![]() ,
имеет вид
,
имеет вид
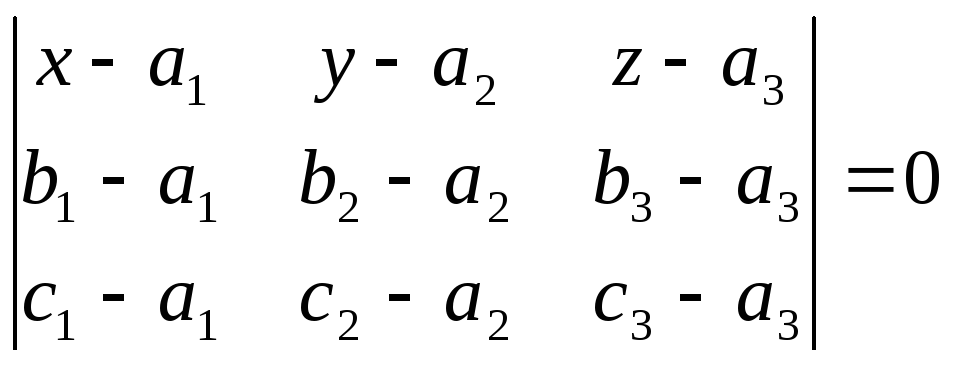 .
.
В нашем случае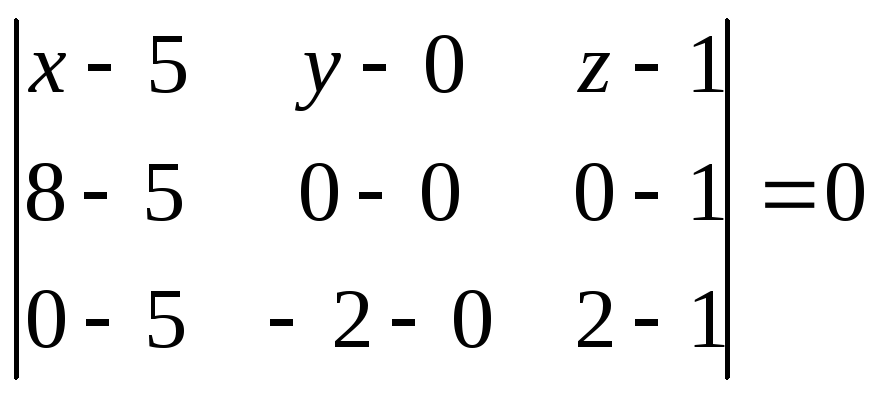 ,
т.е.
,
т.е.
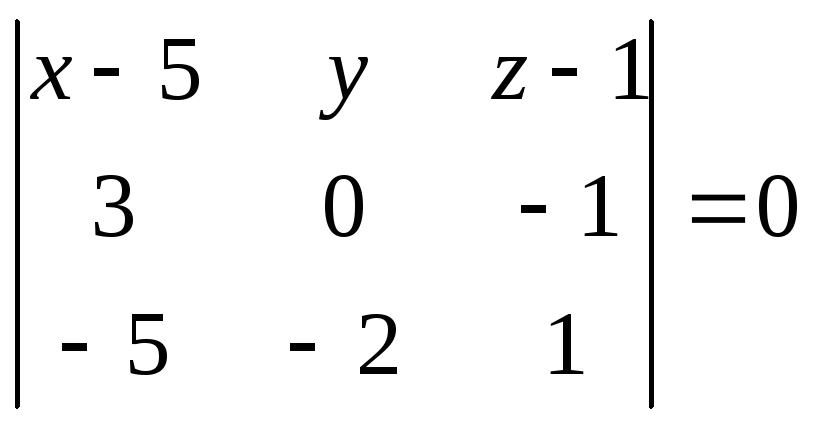 .
.
Раскрыв этот определитель, получим:
![]() или
или
![]() .
.
Уравнение плоскости, прохоедящей через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() имеет вид:
имеет вид:
![]() .
Значит, уравнение плоскости
.
Значит, уравнение плоскости
![]() есть:
есть:
![]() т.е.
т.е.
![]() .
.
Из уравнений плоскостей
![]() ,
,
![]() ,
,
![]() составим систему:
составим систему:
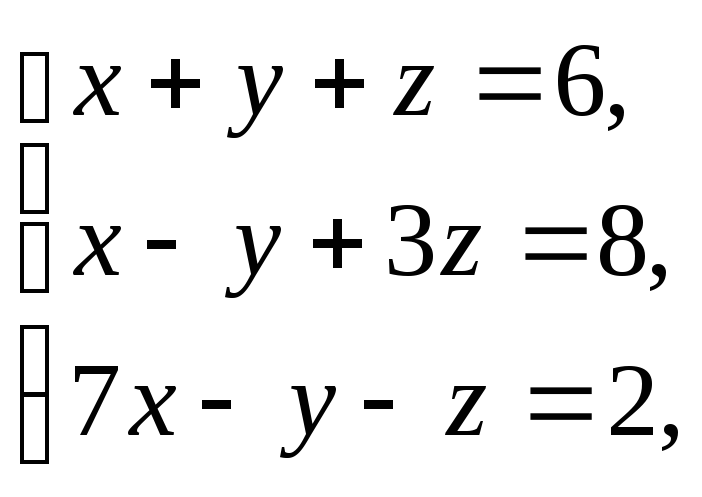
которую и нужно решить. Для решения воспользуемся правилом Крамера. Для этой цели вычислим определители:
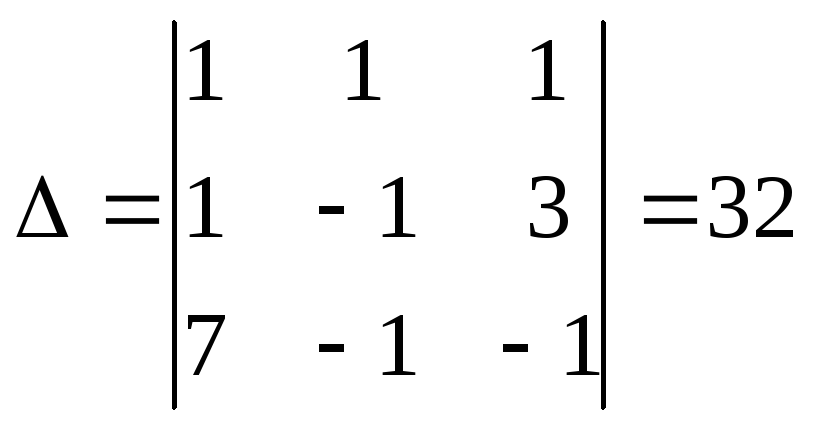 ,
,
![]()
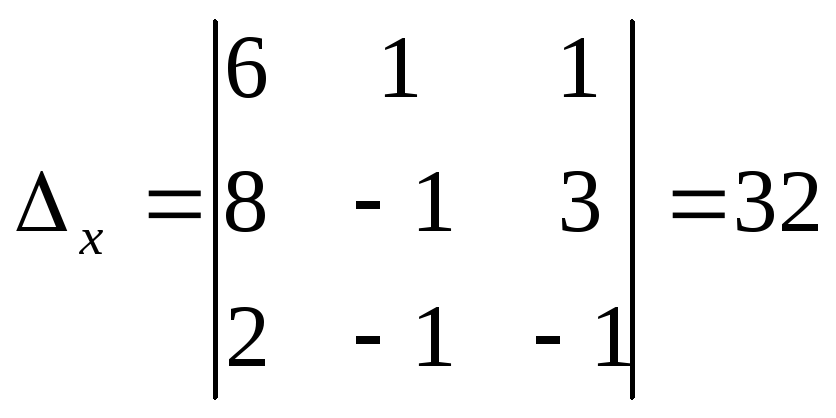 ,
,
 ,
,
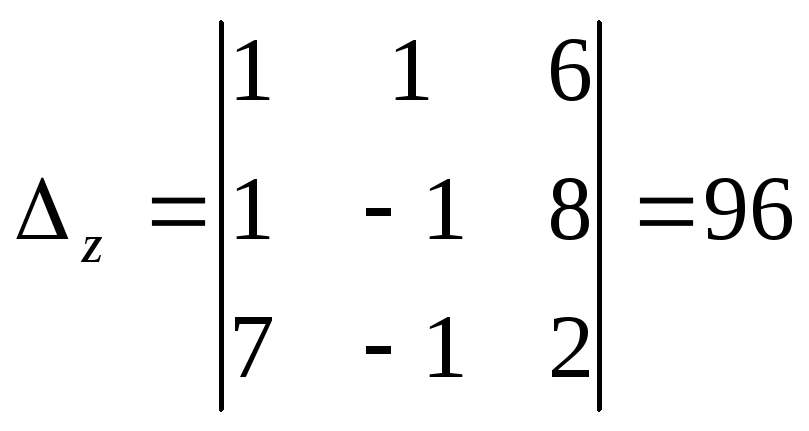 .
.
Значит,
![]() .
Следовательно, плоскости
.
Следовательно, плоскости
![]() ,
,
![]() ,
,
![]() пересекаются в единственной точке
пересекаются в единственной точке
![]() .
.
Задача 4. Дана точка
![]() ,
плоскость
,
плоскость
![]() и прямая
и прямая
![]() .
Найти:
.
Найти:
-
точку
 ,
симметричную точке
,
симметричную точке
 относительно данной плоскости,
относительно данной плоскости, -
точку
 ,
симметричную точке
,
симметричную точке
 относительно данной прямой,
относительно данной прямой,
3) угол между данными прямой и плоскостью,
4)точки пересечения прямой, параллельной
заданной и проходящей через точку
![]() ,
с координатными плоскостями.
,
с координатными плоскостями.
Решение.![]()
1).Запишем уравнение прямой, проходящей
через точку
![]() и перпендикулярной данной плоскости.
Так как в качестве направляющего вектора
такой прямой можно взять нормальный
вектор плоскости
и перпендикулярной данной плоскости.
Так как в качестве направляющего вектора
такой прямой можно взять нормальный
вектор плоскости
![]() ,
то уравнение прямой запишется в виде:
,
то уравнение прямой запишется в виде:
![]() .
Найдем точку
.
Найдем точку
![]() пересечения
этой прямой и данной плоскости, которая
будет проекцией точки
пересечения
этой прямой и данной плоскости, которая
будет проекцией точки
![]() на
данную плоскость. Для этого надо решить
совместно систему уравнений:
на
данную плоскость. Для этого надо решить
совместно систему уравнений:
![]() ,
,
![]() .
.
Перепишем каноническое уравнение прямой
в параметрической форме, вводя параметр
![]() :
:
![]()
![]() ,
т.е.
,
т.е.![]() .
Подставляя эти выражения для
.
Подставляя эти выражения для
![]() в уравнение плоскості, получим
в уравнение плоскості, получим
![]() ,
откуда
,
откуда
![]() - координаты точки
- координаты точки
![]() .
.
Так как точка
![]() является серединой отрезка
является серединой отрезка
![]() ,
то координаты
,
то координаты
![]()
![]() симметричной точки найдутся из формул
симметричной точки найдутся из формул
![]() ,
откуда
,
откуда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
3).Найдем уравнение плоскости, проходящей
через точку
![]() и перпендикулярной данной прямой. Так
как в качестве нормального вектора
такой плоскости можно взять направляющий
вектор
и перпендикулярной данной прямой. Так
как в качестве нормального вектора
такой плоскости можно взять направляющий
вектор
![]() данной прямой, то уравнение плоскости
запишется в виде:
данной прямой, то уравнение плоскости
запишется в виде:
![]() или
или![]() .
.
Найдем точку
![]() пересечения этой плоскости и заданной
прямой, которая будет проекцией точки
пересечения этой плоскости и заданной
прямой, которая будет проекцией точки
![]() на
данную прямую. Для этого надо решить
систему уравнений:
на
данную прямую. Для этого надо решить
систему уравнений:
![]() ,
,
![]() .
Как и в п.1 записываем уравнение прямой
в параметрическом виде:
.
Как и в п.1 записываем уравнение прямой
в параметрическом виде:![]() и
подставляем
и
подставляем
![]()
![]() в уравнение плоскости
в уравнение плоскости![]() или
или
![]()
![]() .
Отсюда
.
Отсюда
![]() и
и
![]() .
.
Координаты
![]() симметричной точки
симметричной точки
![]() находим, используя формулы для координат
середины отрезка, т.е.
находим, используя формулы для координат
середины отрезка, т.е.
![]()
![]() ,
откуда
,
откуда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
3).Угол
![]() между плоскостью
между плоскостью
![]() и
прямой
и
прямой
![]() вычисляется по формуле
вычисляется по формуле
![]() ,
откуда
,
откуда
![]() .
.
4). Уравнение прямой, проходящей через
точку
![]() ,
параллельно прямой
,
параллельно прямой
![]() записывается в виде
записывается в виде
![]() .
Чтобы найти точку
.
Чтобы найти точку
![]() пересечения этой прямой с плоскостью
пересечения этой прямой с плоскостью
![]() ,
надо в уравнениях прямой положить
,
надо в уравнениях прямой положить
![]() :
:
![]()
![]() ,
откуда
,
откуда
![]() .
Следовательно,
.
Следовательно,
![]() .
.
