Перша частина

Завдання 1.1 - 1.16 містять по чотири варіанти відповідей, з яких ОДНА відповідь ПРАВИЛЬНА. Виберіть правильну, на Вашу думку відповідь і відзначте її в бланку відповідей.

1.1. Спростіть вираз

А); Б); В); Г)

1.2. Обчисліть значення виразу

А) 7; Б)-7; В) 14; Г)-14.

1.3. Яка з рівності є тотожністю?

A) cos(π- α)= cosa ; В) cos(π-α)= -cosα;

Б) ; Г)

1.4. Відомо, що . Порівняйте m і n.

А) m < n ; Б) m > n; В) m = n ; Г) m > n .

1.5. Знайдіть загальний вид первісної функції f(x) = 3х².

А) 3х³+С; В) х²+С;

Б) х³+С; Г) 6х + С.

1.6. Вкажіть область визначення функції f(x)= log₉ (7 - х).

А) (7; ∞); Б) (-∞; 7); В) [7; ∞); Г) (-∞; 7].

1.7. Яка геометрична фігура не може служити графіком деякої функції?

А) пряма; Б) точка; В) парабола; Г) коло.

1.8. Яке число є періодом функції у = sin 2x ?

А) ; Б); В) π; Г).

1.9. Розв’яжіть рівняння

А) В)

Б) Г)

1.10. Розв’яжіть нерівність

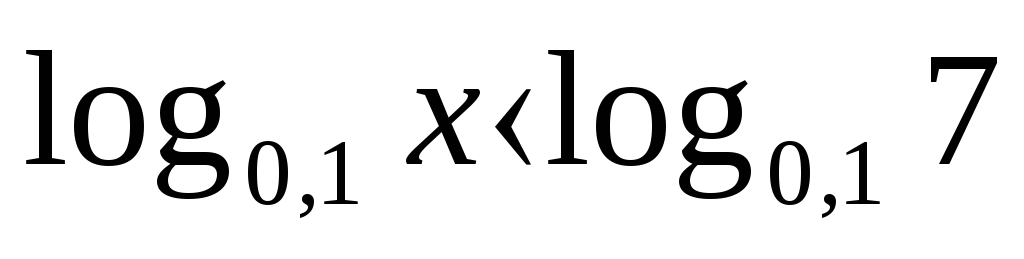
А) (-∞;7); Б)(7; ∞) В) (0;7) Г)(- ∞;∞)

1.11. Спростіть вираз

А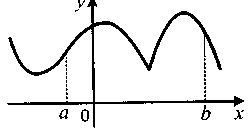)13; Б)13-8; В)11; Г) 11-8.

1.12. Скільки критичних точок на проміжку [а; b] має функція, графік якої зображений на малюнку?

А)3; Б) 2; В) 4; Г) 5.

1.13. У трикутнику ABC АВ=8 см, ВС=10 см, АС=12 см, точка М - середина сторони АВ, точка К - середина сторони ВС. Знайдіть периметр чотирикутника АМКС.

А) 27 см; Б) 21 см; В) 18 см; Г) 15 см.

1.14. Яка величина кута β, зображеного на малюнку, якщо α = 50°?

А) 25°; В) 100°;

Б) 50°; Г) встановити неможливо.

1.15. Обчисліть об'єм правильної трикутної призми, сторона підстави якої рівна 20 см, а висота - 9 см.

А) см³; Б) 300 см³; В) 900 см³; Г) см³.

1.16. Точка С - середина відрізка АВ, А(2;4;6), С(0; 1; 10). Знайдіть координати точки В.

А) В(1; 2,5; 8); Б) В(~2; -2; 14); В) В(-2;-3; 4); Г) В(2; 6; 26).

Друга частина

Розв’язання задач 2.1. – 2.8. повинно містити обґрунтування. В ньому треба записати послідовні логічні дії та пояснення, посилатися на математичні факти, з яких слідує те чи інше твердження. Якщо треба, проілюструйте розв’язання схемами, графіками, таблицями.

2.1. Спростіть вираз

2.2. Знайдіть значення виразу

2.3. Розв’яжіть рівняння

2.4. Знайдіть область визначення функції

2.5. Обчисліть значення похідної функції в точці х₀= -2

2.6. Знайдіть проміжки зростання функції f(x)=

2.7. З точки D, яка лежить поза даною прямої n, проведені до цієї прямої похилі DK, DB, які утворюють з нею кути 45⁰ та 60⁰ відповідно. Знайдіть довжину проекції похилої DK на пряму n, якщо DB=см.

2.8. Сторона основи правильної чотирикутної піраміди дорівнює a, а її діагональний переріз – рівносторонній трикутник. Знайдіть об’єм піраміди.