Частина друга.

Розв’язання задач 2.1. – 2.8. повинно містити обґрунтування. В ньому треба записати послідовні логічні дії та пояснення, посилатися на математичні факти, з яких слідує те чи інше твердження. Якщо треба, проілюструйте розв’язання схемами, графіками, таблицями.

2.1. Знайдіть значення виразу .

2.2. Розв'яжіть рівняння sin 2x + cosx = 0 .

2.3. Спростіть вираз:.

2.4. Чому дорівнює значення похідної функціїв точці х₀ = π?

2.5. Обчисліть інтеграл .

2.6. Розв'яжіть нерівність

2.7. Один із катетів прямокутного трикутника дорівнює 30 см, а радіус описаного навколо нього кола — 17 см. Обчисліть площу даного трикутника.

2.8. В основі конуса проведено хорду, яку видно із центра основи під кутом α, а із вершини конуса — під кутом β. Знайдіть площу бічної поверхні конуса, якщо радіус його основи дорівнює R.

Варіант 20

Частина перша

Завдання 1.1 – 1.16 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь та позначте її у бланку відповідей.

1.1. Скільки коренів має рівняння

А) жодного кореня; Б) один корінь; В) два корені; Г) безліч коренів.

1.2. Порівняйте і

А) < В) >

Б) = Г) порівняти неможливо.

1.3. Яка нерівність не має розв'язків?

А) - lgx > 0; Б) lg(-x) > 0; В) lgx lg(-x); Г) lgx² < 0.

1.4. Обчисліть значення виразу

А) 2,5; Б)1; В) 0; Г) - 1.

1.5. Знайдіть суму коренів рівняння

А) 9; Б) 7; В) -1; Г) 1.

1.6. Три маляра з однаковою продуктивністю праці фарбують 4 однакових стіни за 1 год. За який час один маляр пофарбує одну таку стіну?

А) 5 хв; Б) 15 хв; В) 30 хв; Г) 45 хв.

1.7. Подайте вираз 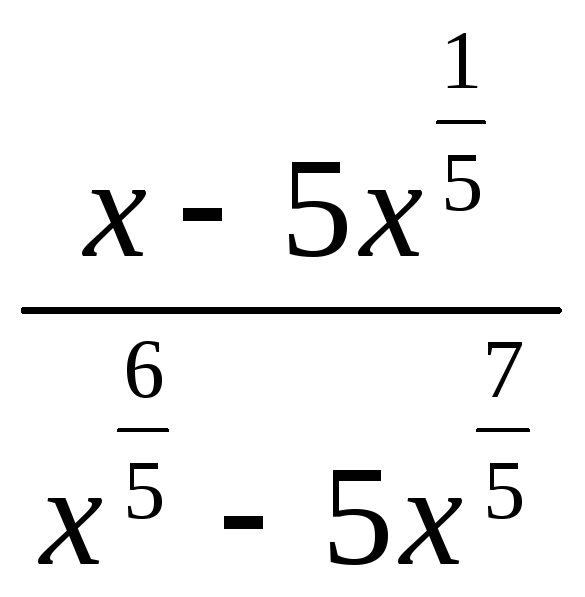у вигляді степеня з раціональним показником.

А) ; Б); В) ; Г).

1.8. Обчисліть інтеграл

А) 0; Б) 2; В) 4; Г) 5.

1.9. Знайдіть похідну функції

А) ; Б); В); Г).

1.10. На рисунку зображено графік функції у = f(x), визначеної на проміж­ку [-7; 6]. Укажіть проміжки зростання даної функції.

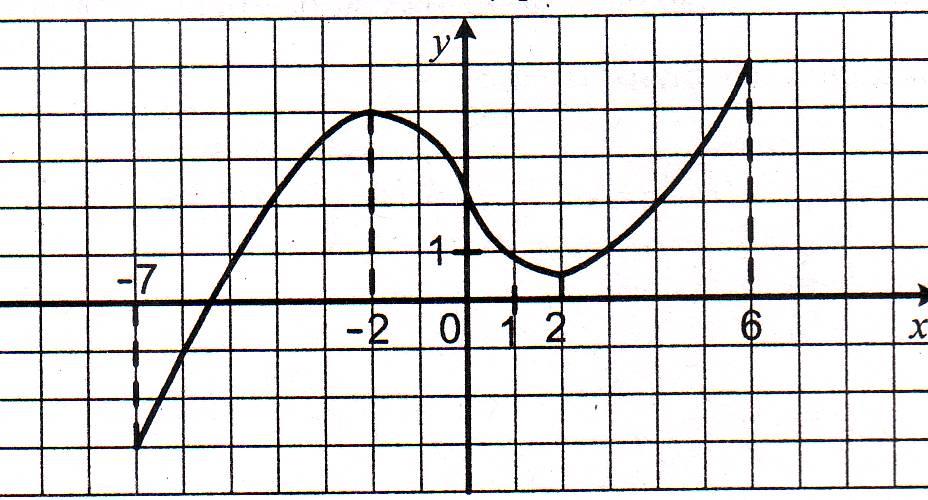
А) [-7;-2] і [2; 6];

Б) [-2; 2];

В) [-3; 5];

Г) [-5,5; -2] і [2; 6].

1.11. Яка множина значень функції у = 4 - (х + 1)²?

А) (-∞;4]; Б) [4; ∞); В) (-∞;-1]; Г) [-1; ∞).

1.12. Спростіть вираз

А) ; Б); В); Г) 4.

1.13. Кут між діагоналлю ромба і його стороною дорівнює 35°. Яка величина найбільшого кута ромба?

А) 110°; Б) 55°; В) 120°; Г) 100°.

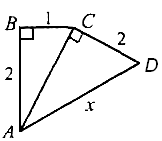
1.14. На рисунку зображено трикутники ABC і ACD такі,

що ABC = ACD = 90°. Яка довжина відрізка х

(довжини відрізків на рисунку наведено в сантиметрах)?

А) см; Б) см; в) 3 см; Г) 2 см.

1.15. Обчисліть об'єм конуса, висота якого дорівнює 4 см, а діаметр основи — 6 см.

А) 48см³; Б) 16см³; В) 36см³; Г) 12см³.

1.16. Який з даних векторів колінеарний вектору (-4; 18; 6)?

А)(2;9;-3); Б) (2;-9; -3); В ) (2;-9; 3); Г) (-2; 9; -3).

Частина друга.

Розв’язання задач 2.1. – 2.8. повинно містити обґрунтування. В ньому треба записати послідовні логічні дії та пояснення, посилатися на математичні факти, з яких слідує те чи інше твердження. Якщо треба, проілюструйте розв’язання схемами, графіками, таблицями.

2.1. Розв’яжіть нерівність: log₉(4-3x) < 0,5.

2.2. Знайдіть корені рівняння:

2.3. Спростіть вираз

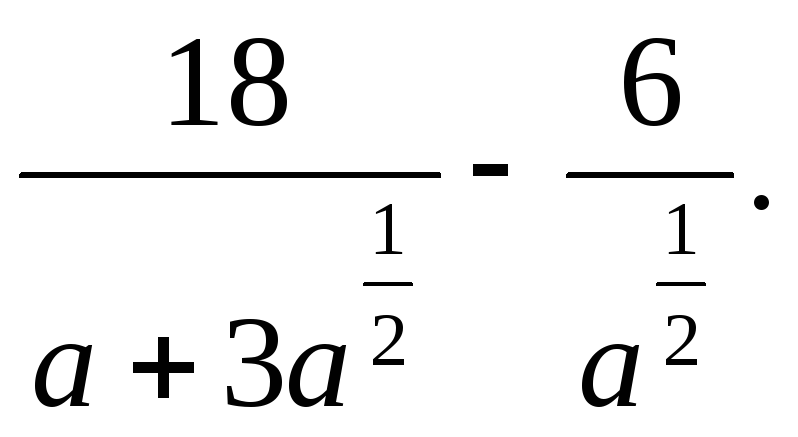
2.4. Обчисліть значення похідної функції f(x) = е^5х + е^-2х в точці х₀ = 0 .

2.5. Розв'яжіть рівняння:.

2.6. Моторний човен пройшов 7 км проти течії річки і 8 км за течією, витративши на весь шлях 1 год. Знайдіть швидкість човна в стоячій воді, якщо швидкість течії річки становить 1 км/год.

2.7. Відрізок AD — бісектриса трикутника ABC, AD = l, C = 90°,BAC = . Знайдіть довжину відрізкаBD.

2.8. Обчисліть площу бічної поверхні правильної чотирикутної призми, діагональ якої дорівнює см і нахилена до площини основи під кутом 30°.

Варіант 21