
Чем занимается топология. Простейшие топологические инварианты
Отображение f: A -> B называется взаимно однозначным, если в каждую точку множества B отображается точно одна точка множества A. Это означает, что, во-первых, никакие две различные точки множества A не переходят в одну и ту же точку множества B (не “склеиваются” при отображении f) и, во-вторых, каждая точка множества B поставлена в соответствие некоторой точке множества A (то есть A отображается на все множество B, а не на его часть).
Для взаимно однозначного отображения f: A -> B можно определить обратное отображение f -1: B -> A (которое каждой точке y, принадлежащей B, ставит в соответствие точку множества A, переходящую в y при отображении f).
Отображение f: A -> B называется гомоморфным отображением (или гомоморфизмом), если оно, во-первых, взаимно однозначно и, во-вторых, взаимно непрерывно, то есть не только само отображение f непрерывно, но и обратное отображение f -1 также непрерывно.
Наглядно гомоморфизм можно представлять себе как такое отображение одного множества на другое, которое происходит и без разрывов, и без склеиваний. Например, будем считать, что фигуры A, B “изготовлены” из очень прочного и эластичного материала, и будем допускать любые растяжения и искривления этого материала без разрывов и без образования складок и склеек; если мы сможем при этих условиях “наложить” фигуру A на B, то они гомоморфны. Так, контур треугольника (или, вообще, любого многоугольника) гомоморфен окружности.
Пример 1. Поверхность шара, поверхность куба, цилиндра — все гомоморфны между собой. Однако эти поверхности не гомоморфны тору (который можно наглядно представить себе как поверхность баранки или автомобильной камеры. Поверхность гири гомоморфна тору.
Пример 2. Будем представлять себе буквы русского алфавита в виде линий. Буквы Г, Л, М, П, С гомоморфны между собой. Буквы Е, У, Т, Ч, Ш, Ц, Э также гомоморфны между собой, но не гомоморфны указанным ранее буквам. Буква О не гомоморфна никакой другой букве русского алфавита.
Пример 3. Пусть A — полуокружность с центром O, из которой исключены концевые точки m и n, а B — касательная полуокружности, параллельная диаметру mn (рис. 31.1). Центральное проектирование p: A -> B из центра O есть гомоморфное отображение. Таким образом, прямая гомоморфна полуокружности без концевых точек.

В свою очередь полуокружность гомоморфна отрезку (ее можно распрямить). Следовательно, прямая гомоморфна открытому отрезку (то есть отрезку, из которого выброшены концевые точки).
Неплохо было бы сравнить понятие гомоморфизма и понятие конгруэнтности фигур. В геометрии рассматриваются отображения, сохраняющие расстояния между точками. Они называются движениями (или перемещениями). В результате движения каждая фигура перекладывается на новое место как твердое целое, без изменения расстояний. Две фигуры, которые переводятся одна в другую (“совмещаются”) с помощью движения, называются конгруэнтными и рассматриваются как одинаковые, как не отличающиеся (с геометрической точки зрения) друг от друга. В топологии рассматриваются отображения, более общие, чем движения, а именно гомоморфные отображения. Две гомоморфные между собой фигуры рассматриваются (с топологической точки зрения) как одинаковые, не отличающиеся друг от друга. Те свойства фигур, которые не изменяются при гомоморфных отображениях, называются топологическими свойствами фигур, или тинвариантами (от латинского слова invariant — неизменный). Изучением топологических свойств фигур и занимается топология.
Простейшие топологические инварианты
Выше, рассматривая пример 1, мы говорили, что поверхность шара (сфера) не гомоморфна тору, и вряд ли у читателя возникло сомнение в этом. Но как доказать, что две фигуры не являются гомоморфными? Ведь из того, что мы не сумели найти гомоморфного отображения одной фигуры на другую, не вытекает еще с достоверностью, что такого гомоморфного отображения не существует.
Для доказательства того, что две фигуры не гомоморфны друг другу, пользуются топологическими инвариантами. Пусть, например, с помощью некоторого правила каждой фигуре ставится в соответствие определенное число, причем так, что числа, соответствующие двум гомоморфным фигурам, всегда оказываются равными. Тогда это число выражает некоторое свойство фигуры, сохраняющееся при гомоморфных отображениях, то есть являющееся топологическим инвариантом. Если теперь две фигуры A и B таковы, что соответствующие им числа оказались различными, то эти фигуры не могут быть гомоморфными.
Пример 4. Буква Ы представляет собой фигуру, состоящую из двух «кусков», из двух не связанных между собой частей. Остальные буквы русского алфавита, кроме Й, Ё, состоят из одного связного куска. Число связных «кусков», из которых состоит фигура (говорят также: число компонент фигуры), является топологическим инвариантом; если две фигуры гомоморфны, то обе они состоят из одинакового числа компонент. Поэтому буква Ы не гомоморфна, например, букве О, букве П, букве Ц и так далее.
Пример 5. На фигуре восьмерки имеется такая точка x, что после удаления из восьмерки точки x вместе с близлежащими точками (рис. 31.2, слева) мы получаем несвязную фигуру (содержащую более одной компоненты). Точку, обладающую этим свойством, называют разбивающей точкой фигуры. Никакая отличная от x точка x* восьмерки не является разбивающей (рис. 31.2, справа).
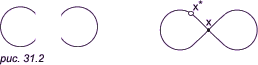
Понятия «разбивающая точка», «неразбивающая точка» топологически инвариантны: если x есть разбивающая точка фигуры A, а f: A -> B — гомоморфное отображение, то f(x) есть разбивающая точка фигуры B. Поэтому число разбивающих точек данной фигуры есть ее топологический инвариант, число неразбивающих точек — также топологический инвариант.
Пример 6. Рассмотрим сферу, в которой вырезано p круглых дыр, и заклеим каждую из дыр ручкой. Полученная поверхность (рис. 31.3, a) называется сферой с p ручками. Сфера с одной ручкой гомоморфна тору (рис. 31.3, b), а сфера с двумя ручками — поверхности «кренделя» (получающейся склеиванием двух ручек, рис. 31.3, c).

