Econometrics

Задачі

Група А

Перевірити наявність гетероскедастичності залишків за критерієм Голдфелда-Квондта, розбивши всі спостереження на 2 групи по 8 елементів в кожній, α = 0, 01.

51

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність виявлено, то оцінити модель за зваженим методом найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

1. Перевірити наявність гетероскедастичності залишків для моделі yt = β0 + β1xt + vt за критеріями (α = 0, 01):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

52

2. Якщо гетероскедастичність виявлено, то оцінити модель за зваженим методом найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

Задача 3.6. На основі даних задачі 1.15

1.визначити наявність гетероскедастичності за критеріями (α = 0, 01):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність присутня, то оцінити модель за допомогою зваженого методу найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

Задача 3.7. На основі даних задачі 1.16

1.визначити наявність гетероскедастичності за критеріями (α = 0, 05 ):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність присутня, то оцінити модель за допомогою зваженого методу найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

Задача 3.8. На основі даних задачі 1.18

1.визначити наявність гетероскедастичності за критеріями (α = 0,1):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність присутня, то оцінити модель за допомогою зваженого методу найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

53

Задача 3.9. На основі даних задачі 1.20

1.визначити наявність гетероскедастичності за критеріями (α = 0, 05 ):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність присутня, то оцінити модель за допомогою зваженого методу найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

Задача 3.10. На основі даних задачі 2.20

1.визначити наявність гетероскедастичності за критеріями (α = 0, 05 ):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність присутня, то оцінити модель за допомогою зваженого методу найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

Задача 3.11. На основі даних задачі 2.27

1.визначити наявність гетероскедастичності за критеріями (α = 0,1):

•Голдфелда-Квондта;

•Глейзера;

•Уайта.

2.Якщо гетероскедастичність присутня, то оцінити модель за допомогою зваженого методу найменших квадратів, використовуючи оцінки вагів у формі

•Глейзера;

•Уайта.

54

Тема 4. Модель лінійної регресії з автокорельованими збуреннями

Основні визначення

Вид моделі.

yi = β0 + β1xi1 +…+ βk −1 xi,k −1 + vi , i = 1, n ,

вякій вектор збурень не задовольняє класичним властивостям збурень:

1.Mvi = 0

2.Гомоскедастичність: D vi = Mvi2 = σ2 = const ,i = 1, n .

3.Залежність збурень: cov (vi , vj )≠ 0 .

4.Незалежність збурень та регресорів: cov (vi , xij )= 0, i, j .

5.Збурення vi нормально розподілені для всіх i.

Наслідки автокорельованості збурень на оцінки методу найменших квадратів:

1.Оцiнки МНК будуть незміщеними, але не будуть ефективними (не матимуть найменшої дисперсії).

2.Стандартнi оцінки коварiацiйної матриці оцінки МНК будуть зміщеними, i, як наслідок, процедури перевірки гіпотез та інтервального оцінювання, основані на стандартних статистиках, будуть некоректними.

Критерій визначення автокорельованості збурень Дарбіна-Уотсона.

Підраховується практичне значення статистики Дарбіна-Уотсона

n

∑(vˆi − vˆi−1)2

i=1

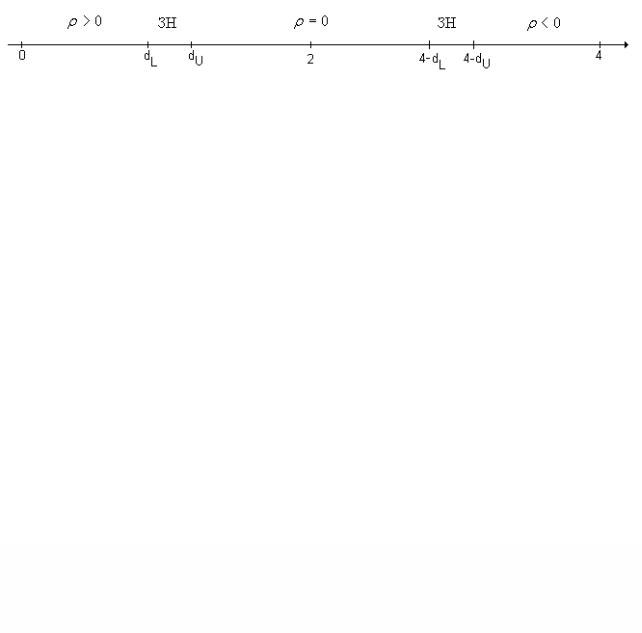
Зтаблиці Дарбіна-Уотсона знаходиться два числа dL таdU . В залежності

від розташування точок на координатній прямій робиться висновок.

Робимо висновок за таким правилом:

Якщо d < dL, то має місце автокореляція з додатнім ρ.

Якщо dL < d < dU, то ми не можемо зробити ніякого висновку, і цей інтервал називається зоною невизначеності (ЗН).

Якщо dU < d< 4 – dU, то автокореляція відсутня.

Якщо 4 – dU < d < 4–dL, то ми не можемо зробити ніякого висновку. Цей інтервал також є зоною невизначеності (ЗН).

Якщо 4 – dL < d < 4, то має місце автокореляція з від’ємним ρ.

55

На практиці, якщо вибіркове значення d потрапляє до зони невизначеності (ЗН), то вважають, що має місце автокореляція.

Узагальнений метод найменших квадратів.

Оцінкою узагальненого МНК коефіцієнтів моделі (1) називається оцінка звичайного МНК, знайдена за моделлю (2).

Процес авторегресії першого порядку AR(1). vi = ρvi−1 + εi ,i = 1, n .

У випадку AR(1)–збурень кореляційна матриця Σ записується у вигляді

Це дає можливість знайти змінні для узагальненого методу найменших квадратів у явному вигляді:

Якщо у вихідній моделі є постійний доданок, то перетворена модель не матиме константи. Замість неї з’явиться зміннаx0* , значення якої дорівнюють

x10* = 1 − ρ2 ,

xi*0 = 1 − ρ, 2 ≤ i ≤ n .

Оцінка параметра ρ .

Вибірковий коефіцієнт кореляції залишків методу найменших квадратів

56

Оцінка Дарбіна-Уотсона.

ρˆ = 1 − d2 .

Метод Дарбіна.

Формула (*) записується у вигляді

yt = β1 (1 − ρ)+ ρyt −1 + β2 xt ,2 − ρβ2 xt −1,2 +…+ βk −1xt,k −1 − ρβk −1 xt,k −1 + vt ,

тобто yt −1 включається в число регресорів, а ρ – в число параметрів, що оцінюються. Для цієї регресії за допомогою звичайного МНК знаходяться

Можна покращити якість оцінок βˆj , підставивши отримане значення ρˆ до (*), і знайти нові МНК-оцінки параметрів βˆj .

Метод Кочрейна-Оркатта.

Ітеративно обраховуються формули (*), залишки за узагальненим методом найменших квадратів, поки не буде досягнуто необхідної точності.

Метод Хілдрета-Лу.

Обчислюється модель при всіх ρ з інтервалу від -1 до 1 з кроком 0.01. Вибирається те значення, при якому сума квадратів відхилень в узагальненому методі найменших квадратів мінімальна.

Приклад розв'язання задачі

Приклад 1.

На базі даних по грошовій масі М2 та ВВП України побудувати модель ln Mi = β0 + β1 lnYi + vi , перевіривши залишки на наявність автокореляції.

57

Перетворюємо вхідну інформацію, знайшовши логарифми від початкових

даних. За звичайним МНК оцінюємо модель ln Mi = β0 + β1 lnYi + vi : ln Mi = −0, 027 + 0,906lnYi .

Знаходимо вектор залишків

ˆvi = ln Mi + 0, 027 − 0,906lnYi .

Обраховуємо статистику Дарбіна-Уотсона:

dL =1, 33, dU = 1, 48 , тому робимо висновок про наявність додатної автокореляції.

Оцінимо коефіцієнт кореляції:

ρˆ =1 − d = 0, 661 2 .

Обраховуємо скориговані значення змінних за формулами:

ln M1* = 1 − ρ2 ln M1 ,

ln Mi* = ln Mi − ρln Mi−1, 2 ≤ i ≤ 28 .

Y1* = 1 − ρ2Y1 ,

Yi* = Yi − ρYi−1, j , 2 ≤ i ≤ 28 .

C1* = 1 − ρ2 ,

Ci* =1 − ρ, 2 ≤ i ≤ 28.

58

Задачі

Група А

Задача 4.1. Знайдіть математичне сподівання, дисперсію та коваріацію першого порядку для стаціонарного AR (1) процесу yt = µ +ϕ1 yt −1 + εt .

Обчислити коваріації перших чотирьох порядків для AR (1)

yt = µ +ϕ1 yt −1 + εt .

Обчислити коваpіаційну матpицю для пpоцесу AR(2).

1.Показати, що така оцінка є лінійною та незміщеною.

2.Обчислити дисперсію цієї оцінки та показати, що стандартна оцінка цієї дисперсії є зміщеною.

59

Показати, що для регресії y = X β + v з автокорельованими збуреннями першого порядку vt = ρvt −1 + εt найкращим прогнозом на наступний період буде

Перевірити модель на наявність автокореляції збурень.

модель yt = β0 + β1xt + vt :

yt = 2,1 + 0, 7xt ,

обраховано значення статистика Дарбіна-Уотсона d = 0, 72 . Визначити найкращий прогнозˆy31 .

Група Б

Задача 4.9. Для поданих даних оцінити параметри макроекономічної виробничої функції Коба-Дугласа.

1.За допомогою критерію Дарбіна-Уотсона перевірити гіпотезу про відсутність автокореляції збурень, α = 0, 05 .

2.У випадку наявності автокореляції оцінити модель за допомогою узагальненого методу найменших квадратів.

60