
черняк
.pdf2. У разі наявності автокореляції оцініть параметри моделі узагальненим методом найменших квадратів, оцінивши параметр методом Кочрейна – Оркатта.
Задача 5.15. За даними задачі 2.15:
1.Визначте наявність автокореляції залишків 0,01.
2.У разі наявності автокореляції оцініть параметри моделі, використовуючи модель нелінійної регресії (5.24).
Задача 5.16. За даними задачі 2.18:
1.Визначте наявність автокореляції залишків 0,01.
2.У разі наявності автокореляції оцініть параметри моделі узагальненим методом найменших квадратів, оцінивши параметр методом Дурбіна – Уотсона.
147

Розділ 6. Системи одночасних рівнянь
6.1. Приклади систем одночасних рівнянь в економіці
Під час моделювання достатньо складних економічних об'єктів доводиться використовувати не одне, а кілька взаємопов'язаних рівнянь, тобто описувати модель за допомогою цілої системи рівнянь. Частина рівнянь системи одночасних рівнянь складаються з рівнянь поведінки, які описують залежності певних факторів, і рівнянь- тотожностей, які відображають певну економічну структуру.
В економіці існує багато прикладів таких систем. Однією з найпростіших є модель Хаавелмо, яка досліджує взаємозалежність між споживанням, інвестиціями та ВВП країни:
Ct Yt ut ,Yt Ct It ,
де It – інвестиції; Ct – споживання; Yt – ВВП країни в період t .
Перше рівняння являє собою залежність між споживанням товарів і послуг та доходами країни. Друге рівняння є рівнянням-тотожністю, тому що показує, що в закритій економіці ВВП країни має дорівнювати споживанню та інвестиціям. Очевидно, що оцінювати лише одне перше рівняння буде некоректним, адже в такому разі не буде виконано умову другого рівняння. Таким чином, для аналізу такої моделі слід розробити додатковий економетричний апарат.
У моделі акселератора досліджено складніші залежності у відкритій економіці:
Ct Yt 1 ut ,It Ct Ct 1 vt ,Yt Ct It Xt ,
де It – інвестиції; Ct – споживання; Xt – чистий експорт; Yt – ВВП країни в період t .
Уцій моделі споживання залежить не від рівня поточних доходів, а від рівня попереднього періоду, що робить можливим динамічний аналіз. Інвестиції визначають пропорційно до приросту споживання. Нарешті, третє рівняння показує тотожність ВВП і суми споживання, інвестицій і чистого експорту. Очевидно, що коли оцінити лише одне з рівнянь, то це не зможе гарантувати виконання останньої умови, а тому треба вміти оцінювати всі три рівняння разом.
У1950 р. Л. Клейн запропонував динамічну модель макроекономіки:
|
|
|
|
|
|
|
0 1Pt 2Pt 1 3 Wt |
p |
|
|
|
|
|
g |
1t , |
||||||||||||||||||||
|
|
|
|
|
Ct |
|
Wt |
|
|||||||||||||||||||||||||||
|
|
|
|
|
I |
t |
|
P |
P |
|
|
|
3 |
K |
t 1 |
|
2t |
, |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
p |
0 |
|
1 |
t |
|
|
2 |
t 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
X |
|
|
|
A |
|
|
|
, |
|
|
|
|
|||||||||
|
|
|
|
|
W |
|
0 |
t |
2 |
t 1 |
3 |
3t |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Xt |
Ct It Gt , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
X |
|
T |
|
W p |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
P |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
t |
|
|
|
t |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Kt |
Kt 1 It , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
де I |
t |
– |
інвестиції; |
C |
– споживання; |
|
X |
t |
– |
чистий експорт; |
|
|
W p |
– зарплата в приватному |
|||||||||||||||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
||
секторі; |
W g – зарплата в державному |
|
секторі; |
|
G |
t |
– |
|
державні |
видатки, що не містять |
|||||||||||||||||||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зарплату; Pt – дохід від приватного сектору; Kt – капітал; Yt |
|
– ВВП країни в період t ; At – |
|||||||||||||||||||||||||||||||||
тренд. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За допомогою цієї моделі було створено сценарії розвитку США в середині ХХ-го століття.
Укласичній моделі попиту та пропозиції досліджено рівняння попиту та пропозиції
встані рівноваги:
148
|
d |
|
|
p y |
(1) |
, |
|
|
||
q |
t |
0 |
t |
|
|
|
||||
|
|
1 t |
2 t |
|
|
|
|
|||
|
s |
|
|
|
(2) |
|
|
|
|
|
|
|
|
, t 1,n, |
|||||||
qt |
0 1pt 2zt t |
|
||||||||
qd |
qs |
, |
|
|
|
|
|
|
||
|
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де qtd – обсяг попиту; pt – ціна товару; yt – особистий дохід; qts – обсяг пропозиції; zt –
неціновий фактор, який впливає на пропозицію (наприклад, у моделі, яка вивчає попит на сільськогосподарський товар, змінна z може означати кількість опадів). Перше співвідношення – це функція попиту, друге – функція пропозиції, останнє – тотожність локальної ринкової рівноваги. Очевидно, що як і в попередніх прикладах, недоцільно оцінювати кожне рівняння окремо.
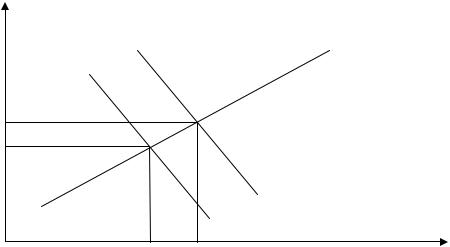
Якщо розглянути систему детальніше, то виявиться, що рівняння суттєво відрізняються від звичайних економетричних регресій. Наприклад, якщо відбудеться певний шок на рівень попиту, то це призведе до зсуву функції попиту від положення D1 до положення D2 (див рис. 6.1). У цьому разі рівноважна ціна має зрости до нового рівня, який відповідає перетину функції пропозиції та нової функції попиту D2. Це означає, що при цьому зростає ціна на продукцію, тобто іншими словами, у рівнянні попиту збурення корельовані з регресором p. Це означає, що порушена четверта умова щодо класичних збурень.
q
D2
S
D1
S |
D1 |
p
Рис. 6.1. Вплив зсуву функції попиту на ціну
Теорема. Якщо регресори корельовані зі збуреннями, то оцінки методу найменших квадратів будуть не тільки зміщеними, а й неспроможними (тобто навіть за наявності масиву даних нескінченої довжини неможливо знайти точні оцінки регресійних коефіцієнтів).
Згідно з наведеною теоремою стає зрозумілим, що слід знаходити спеціальні методи оцінювання наведених систем.
Серед змінних, які входять до систем одночасних рівнянь, розрізняють ендогенні й екзогенні. Значення ендогенних змінних визначають у моделі, а значення екзогенних змінних – за межами моделі. До групи екзогенних змінних також належать лагові значення ендогенних змінних (значення ендогенних змінних у попередні моменти часу). Ендогенні змінні корельовані зі збуреннями в рівняннях, а екзогенні – некорельовані. У цьому останні подібні до незалежних змінних у звичайних регресійних моделях.
6.2. Структурний вигляд системи одночасних рівнянь
У структурному вигляді системи одночасних рівнянь кожне рівняння відображає певний елемент структури економічної системи, що її розглядають, і має економічну інтерпретацію. У зведеному вигляді системи одночасних рівнянь у кожному рівнянні ліворуч стоїть ендогенна змінна, а праворуч – лише екзогенні змінні.
Структурний вигляд систем рівнянь необхідний для проведення економічного аналізу, а зведений – для знаходження коефіцієнтів моделей. Таким чином, зведений вигляд
149

фактично є допоміжним, проте, без нього фактично неможливо правильно ідентифікувати й оцінити модель.
Одна з основних ідей, яка допомагає перейти від структурного виду до зведеного – вираження ендогенних змінних моделі через екзогенні змінні за допомогою стандартних алгебраїчних перетворень.
Розглянемо перехід від структурного до зведеного вигляду на прикладі моделі попиту та пропозиції:
|
|
|
|
|
d |
|
|
p y |
(1) |
, |
|
|
|
|
|
|
|||
|
|
|
|
q |
t |
0 |
t |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
t |
2 t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
s |
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, t 1,n, |
|
|
|
|
|||||||
|
|
|
|
qt |
0 1pt 2zt t |
|
|
|
|
|
|||||||||
|
|
|
|
qd |
qs |
, |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
qd |
– обсяг попиту; |
p |
– ціна товару; y |
t |
– особистий дохід; |
qs |
– обсяг пропозиції; z |
t |
– |
|||||||||
|
t |
|
t |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
||
неціновий фактор, який впливає на пропозицію.
У результаті останньої тотожності систему можна переписати в такому вигляді:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
qt |
0 |
1pt 2yt t |
, |
|
|
|
|
|
|||||||||||||||
|
t 1,n |
(6.1) |
||||||||||||||||||||||
|
|
|
|
|
|
|
p z |
|
|
(2), |
|
|||||||||||||
|
q |
t |
|
t |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0 |
|
|
1 |
t |
|
2 |
t |
|
|
|
|
|
|
|
|||||
Змінні p і q ендогенні, а y і z |
|
– екзогенні. Віднімемо почленно друге рівняння від |
||||||||||||||||||||||
першого: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 , |
||
0 |
0 |
|
|
|
p y z |
t |
||||||||||||||||||
|
|
|
|
|
0 |
|
|
1 |
1 |
|
t |
|
|
2 |
t |
|
2 |
|
t |
t |
||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
||
|
|
|
|
0 |
|
|
|
|
|
y |
t |
|
|
|
z |
t |
|
|
||||||
p |
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
2 |
|
t |
|
|
t . |
(6.2) |
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
1 |
|
|
|
1 |
1 |
|
1 |
1 |
|
|||
Тепер помножимо перше рівняння на 1 і віднімемо від нього друге рівняння,
помножене на 1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 , |
||||
q |
t |
|
|
y |
z |
t |
||||||||||||||
|
|
1 |
1 |
|
0 1 |
1 0 |
|
2 0 t |
|
0 2 |
1 |
t |
1 |
t |
||||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
||||
|
|
|
|
|
|
y |
z |
|
|
|||||||||||
qt |
|
|
|
0 1 |
1 0 |
|
2 1 t |
|
2 1 t |
|
|
1 t |
|
1 |
t |
. |
|
(6.3) |
||
|
|
|
|
|
|
|
1 1 |
|
|
|||||||||||
|
|
|
|
|
1 1 |
|
|
1 1 |
1 1 |
|
|
|
|
|
||||||
Формули (6.2) і (6.3) коректні за умови 1 1 . Останнє співвідношення гарантоване з економічних міркувань, оскільки 1 і 1 мають бути з різними знаками, як коефіцієнти
при ціні у функціях попиту та пропозиції. Зробимо такі позначення:
11 0 0 ,1 1
12 1 2 1 ,
13 1 2 1 ,
21 0 1 1 0 ,1 1
22 2 1 ,1 1
23 2 1 ,1 1
(1) t1 t2 ,
1 1
150

(2) 1 t1 1 t2 .1 1
Ураховуючи введені позначення, маємо
p |
|
|
y |
|
|
z |
t |
(1), |
|
|
|
t |
11 |
12 |
t |
13 |
|
t |
(6.4) |
||
|
|
|
|
y |
z (2). |
|||||
q |
t |
|
|
|
||||||
|
21 |
22 |
23 |
|
|
|
t |
|
||
Отримана система (6.4) – це рівняння зведеного вигляду. Оскільки в рівняннях зведеного вигляду праворуч стоять лише екзогенні змінні, некорельовані зі збуреннями, то ці рівняння коректно оцінювати за допомогою звичайного методу найменших квадратів.
6.3. Ідентифікація рівнянь
Для визначення методу оцінювання системи рівнянь треба ввести поняття ідентифікованості.
Зодного боку, будь-яка система одночасних рівнянь має задовольняти умові повноти,
асаме: кількість рівнянь має збігатися з кількістю ендогенних змінних у системі.
Зіншого боку, в основу класифікації систем рівнянь щодо ідентифікованості покладено можливість виразити коефіцієнти рівнянь структурного вигляду через коефіцієнти рівнянь зведеного вигляду. В одній і тій самій системі деякі рівняння можуть бути ідентифікованими, а деякі – ні. Рівняння називається строго ідентифікованим, якщо його коефіцієнти можна однозначно виразити через коефіцієнти рівнянь зведеного вигляду. Якщо існує більш ніж один розв'язок, то рівняння надідентифіковане. Рівняння буде неідентифікованим, якщо його коефіцієнти неможливо виразити через коефіцієнти рівнянь зведеного вигляду.
Для вираження коефіцієнтів системи через коефіцієнти системи в зведеному вигляді необхідно, щоб кількість рівнянь була не менше за кількість невідомих. Іншими словами, кількість вилучених із рівняння у зведеному вигляді екзогенних змінних має бути не менше за кількість залучених ендогенних змінних мінус одиниця. Така вимога отримала назву порядкової умови ідентифікації; це необхідна, але недостатня умова ідентифікованості рівняння, оскільки, навіть виконуючи його через лінійну залежність рівнянь системи, буде неможливо знайти оцінки коефіцієнтів. Проте необхідною умовою легко користуватися на практиці.
Нехай D – кількість предетермінованих змінних, яких немає в рівнянні, але є в системі; H – кількість ендогенних змінних у рівнянні. Тоді необхідну умову ідентифікованості можна записати в такому вигляді:
якщо D 1 H , то рівняння ідентифіковане;
якщо D 1 H , то рівняння не ідентифіковане;
якщо D 1 H , то рівняння надідентифіковане.
У прикладі системи (6.3) кількість ендогенних змінних у першому рівнянні дорівнює H 1, оскільки до нього входить лише одна ендогенна змінна qt . Водночас до цього
рівняння входять усі екзогенні змінні, тобто жодна зі змінних не вилучена з рівняння, а
тому D 0 |
. Таким чином, |
D 1 0 1 1 H , |
а отже, |
за порядковою |
умовою перше |
|||||
рівняння системи має бути строго ідентифікованим. |
H 1 |
(оскільки введено |
лише одну |
|||||||
Аналогічно для |
другого |
рівняння |
системи |
(4) |
||||||
ендогенну |
змінну |
pt ) і D 0 |
(оскільки жодна з |
екзогенних змінних |
не |
вилучена з |
||||
рівняння). |
Таким |
чином, |
і |
для |
другого |
рівняння |
виконується |
співвідношення |
||
D 1 0 1 1 H , а отже, воно також є строго ідентифікованим.
Проте використання порядкової умови, як було зазначено вище, ще не є достатньою умовою для таких висновків: гарантувати їх може лише рангова умова ідентифікації. Визначник матриці, складений із коефіцієнтів при змінних, відсутніх в цьому рівнянні, не рівний 0, а ранг цієї матриці не менший від кількості ендогенних змінних системи без одиниці.
Для нашого прикладу візьмемо систему (6.1) у структурному вигляді й запишемо матрицю її коефіцієнтів при змінних моделі:
151

|
qt |
pt |
yt |
zt |
|
Перше |
1 |
1 |
a2 |
0 |
|
рівняння |
|||||
Друге |
1 |
|
0 |
|
|
рівняння |
|||||
|
1 |
|
2 |
Визначник матриці коефіцієнтів матриці при змінних, що не входять до досліджуваного рівняння, не має дорівнювати 0, а ранг матриці має дорівнювати кількості ендогенних змінних моделі мінус 1, тобто 2 – 1 = 1.
Для першого рівняння матриця коефіцієнтів при змінних, що не входять до нього, складається лише з одного коефіцієнта: A1 2 . Очевидно, що ранг цієї матриці
дорівнює 1, а визначник матриці – відмінний від 0.
Для другого рівняння матриця коефіцієнтів при змінних, що не входять до нього, складається лише з одного коефіцієнта: A2 2 . Очевидно, що ранг цієї матриці
дорівнює 1, а визначник матриці – відмінний від 0.
Таким чином, достатні умови для системи (6.1) виконано, а отже, можна стверджувати, що обидва рівняння є строго ідентифікованими.
6.4. Оцінювання рівнянь систем
Залежно від ступеня ідентифікованості кожного рівняння системи одночасних рівнянь обирають метод його оцінювання.
Якщо рівняння строго ідентифіковане, то для його оцінювання використовують
непрямий метод найменших квадратів, алгоритм якого може бути таким:
1.Складають зведений вигляд моделі й визначають її коефіцієнти за допомогою звичайного МНК.
2.Шляхом алгебраїчних перетворень повертають до структурного вигляду системи одночасних рівнянь, отримуючи оцінки структурних параметрів.
Щоб отримати оцінки непрямого методу найменших квадратів для моделі (6.1), слід привести її до зведеного вигляду (6.4). Оскільки система (6.4) містить два строго
ідентифіковані рівняння, |
то оцінки tj ,t |
1,2, |
j |
0,2 |
|
|
можна знайти звичайним методом |
||||||||||||||||||||||||||||
найменших квадратів. Після цього знаходять коефіцієнти j , j |
|
|
, |
j , j |
|
. У нашому |
|||||||||||||||||||||||||||||
0,2 |
0,3 |
||||||||||||||||||||||||||||||||||
прикладі |
|
|
|
|
|
|
|
|
|
|
22 , |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
( ) |
|
|
|
22 |
|
23 |
|
, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
12 |
1 |
1 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
13 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
( ) |
|
|
23 |
|
22 |
|
, |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
13 |
1 |
1 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
12 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 1 1 0 |
|
0 1 |
1 0 |
|
0 |
, |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 |
11 |
|
|
21 |
|
|
1 1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
23 |
, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
21 |
|
1 11 |
21 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 1 0 1 |
0 1 1 0 |
13 |
1 0 |
1 0 |
|
|
|
|
|
||||||||||||||||||||||
|
|
21 |
|
, |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
11 |
11 |
|
|
|
1 1 |
|
|
|
|
1 1 |
|
|
1 1 |
|
|
|
|
0 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
22 . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
0 |
|
21 |
|
1 11 |
|
21 |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
||
Далі, підставляючи знайдені за методом найменших квадратів оцінки ˆ tj , t 1, 2, j 0, 2 , отримуємо оцінки непрямого методу найменших квадратів:
ˆ1 ˆ 22 , ˆ 1 ˆ 23 ,
ˆ12 ˆ13
152

ˆ |
|
ˆ |
|
ˆ 22 |
|
|
ˆ 23 |
|
, |
|
|
ˆ |
ˆ |
|
|||||
|
2 |
12 |
|
|
|
||||
|
|
|
|
12 |
|
13 |
|
|
|
ˆ |
|
|
|
ˆ 23 |
|
ˆ 22 |
|
|
|
2 |
ˆ13 |
|
ˆ |
|
|
ˆ |
|
, |
|
|
|
|
|
13 |
|
12 |
|
|
|
ˆ 0 ˆ 21 ˆ 23 ˆ11 ,ˆ13
ˆ 0 ˆ 21 ˆ 22 ˆ11 .ˆ12
Якщо рівняння надідентифіковане, то краще використовувати двохетапний метод найменших квадратів із таким алгоритмом:
1.За допомогою звичайного методу найменших квадратів оцінити регресію кожної ендогенної змінної стосовно набору всіх екзогенних змінних системи.
2.Замість ендогенних змінних, що входять у праву частину рівняння, підставити їхні оцінки, знайдені на першому етапі. Одержані рівняння оцінити за допомогою звичайного методу найменших квадратів.
Для нашого прикладу спочатку слід оцінити регресію виду
pt 0 1yt 2zt t .
Далі обрахувати вибіркову регресійну функцію
pˆ t ˆ 0 ˆ1yt ˆ 2zt .
На другому етапі замість ендогенних змінних, що входять у праву частину рівняння в початковій системі, підставити їхні оцінки, знайдені на першому етапі. Одержане рівняння оцінюємо за допомогою звичайного методу найменших квадратів. У нашому прикладі регресія набуває вигляду
qt 0 1pˆ t 2yt t .
Отримані оцінки ˆ 0,ˆ1,ˆ 2 є оцінками двохетапного методу найменших квадратів.
Слід пам'ятати, що для строго ідентифікованих рівнянь оцінки непрямого методу найменших квадратів і двохетапного методу найменших квадратів збігаються.
Приклад 6.1. Оцінювання системи одночасних рівнянь
Ідентифікувати й оцінити моделі грошового ринку України:
Rt 0 1Yt 2Mt t , Yt 0 1It 2Gt 2t ,
It 0 1Rt 3t ,
на підставі даних за 1998-2003 роки (табл. 6.1).
|
|
|
|
|
|
Таблиця 6.1 |
|
|
|
|
|
|
|
|
|
Рі |
Квар |
ВВП, |
Інвести |
Держа |
M2, |
Облікова |
|
к |
тал |
млн грн |
ції, |
вні |
млн грн |
ставка |
|
|
|
|
млн грн |
витрати, |
|
НБУ на кінець |
|
|
|
|
|
млн грн |
|
періоду, % |
|
|
1 |
2087 |
1744 |
|
1283 |
35 |
|
|
|
1 |
|
6720 |
5 |
|
|
|
2 |
2336 |
2675 |
|
1325 |
41 |
|
1 |
|
7 |
|
7384 |
7 |
|
|
998 |
3 |
2890 |
2877 |
|
1414 |
51 |
|
|
|
8 |
|
8210 |
2 |
|
|
|
4 |
2944 |
6662 |
|
1543 |
82 |
|
|
|
7 |
|
8952 |
2 |
|
|
|
1 |
2498 |
1861 |
|
1563 |
60 |
|
1 |
|
0 |
|
6245 |
1 |
|
|
999 |
2 |
2919 |
3006 |
|
1825 |
60 |
|
|
|
6 |
|
7737 |
8 |
|
|
153
Рі |
Квар |
ВВП, |
Інвести |
Держа |
M2, |
Облікова |
к |
тал |
млн грн |
ції, |
вні |
млн грн |
ставка |
|
|
|
млн грн |
витрати, |
|
НБУ на кінець |
|
|
|
|
млн грн |
|
періоду, % |
|
3 |
3763 |
4023 |
|
2001 |
45 |
|
|
3 |
|
9672 |
9 |
|
|
4 |
3531 |
8662 |
|
2171 |
45 |
|
|
7 |
|
9677 |
4 |
|
|
1 |
3230 |
2659 |
|
2327 |
32 |
|
|
9 |
|
7980 |
5 |
|
|
2 |
3788 |
4018 |
|
2635 |
29 |
2 |
|
9 |
|
10609 |
9 |
|
000 |
3 |
5123 |
5073 |
|
2807 |
27 |
|
|
8 |
|
13271 |
6 |
|
|
4 |
4863 |
11879 |
|
3154 |
27 |
|
|
4 |
|
13763 |
4 |
|
|
1 |
3920 |
3945 |
|
3253 |
25 |
|
|
1 |
|
10506 |
1 |
|
|
2 |
4648 |
6062 |
|
3655 |
19 |
2 |
|
1 |
|
12782 |
2 |
|
001 |
3 |
5899 |
7493 |
|
3929 |
15 |
|
|
9 |
|
15163 |
2 |
|
|
4 |
5950 |
9244 |
|
4518 |
12,5 |
|
|
9 |
|
16186 |
6 |
|
|
1 |
4369 |
4805 |
|
4703 |
11,5 |
|
|
9 |
|
12017 |
2 |
|
|
2 |
4989 |
7268 |
|
5105 |
10 |
2 |
|
3 |
|
14070 |
6 |
|
002 |
3 |
6408 |
7766 |
|
5761 |
8 |
|
|
1 |
|
16853 |
8 |
|
|
4 |
6325 |
17339 |
|
6432 |
7 |
|
|
9 |
|
17270 |
1 |
|
|
1 |
5120 |
6124 |
|
6955 |
7 |
2 |
|
6 |
|
13518 |
2 |
|
2 |
5993 |
9879 |
|
7847 |
7 |
|
003 |
|
7 |
|
16603 |
7 |
|
|
3 |
6541 |
11410 |
|
8584 |
7 |
|
|
3 |
|
18250 |
9 |
|
Розв'язання
Щоб змінні були зіставними, візьмемо логарифми від відповідних величин:
ВВП |
Інвести |
Держав |
Грош |
Облік |
, |
ції, |
ні |
ова |
ова |
Y |
I |
витрати, G |
маса, M |
ставка, |
|
|
|
|
R |
9,95 |
7,46 |
8,81 |
9,46 |
0,35 |
10,0 |
7,89 |
8,91 |
9,49 |
0,41 |
6 |
|
|
|
|
10,2 |
7,96 |
9,01 |
9,56 |
0,51 |
7 |
|
|
|
|
10,2 |
8,80 |
9,10 |
9,64 |
0,82 |
9 |
|
|
|
|
10,1 |
7,53 |
8,74 |
9,66 |
0,60 |
3 |
|
|
|
|
10,2 |
8,01 |
8,95 |
9,81 |
0,60 |
8 |
|
|
|
|
10,5 |
8,30 |
9,18 |
9,90 |
0,45 |
4 |
|
|
|
|
10,4 |
9,07 |
9,18 |
9,99 |
0,45 |
7 |
|
|
|
|
154
10,3 |
7,89 |
8,98 |
10,06 |
0,32 |
8 |
|
|
|
|
10,5 |
8,30 |
9,27 |
10,18 |
0,29 |
4 |
|
|
|
|
10,8 |
8,53 |
9,49 |
10,24 |
0,27 |
4 |
|
|
|
|
10,7 |
9,38 |
9,53 |
10,36 |
0,27 |
9 |
|
|
|
|
10,5 |
8,28 |
9,26 |
10,39 |
0,25 |
8 |
|
|
|
|
10,7 |
8,71 |
9,46 |
10,51 |
0,19 |
5 |
|
|
|
|
10,9 |
8,92 |
9,63 |
10,58 |
0,15 |
9 |
|
|
|
|
10,9 |
9,13 |
9,69 |
10,72 |
0,13 |
9 |
|
|
|
|
10,6 |
8,48 |
9,39 |
10,76 |
0,12 |
9 |
|
|
|
|
10,8 |
8,89 |
9,55 |
10,84 |
0,10 |
2 |
|
|
|
|
11,0 |
8,96 |
9,73 |
10,96 |
0,08 |
7 |
|
|
|
|
11,0 |
9,76 |
9,76 |
11,07 |
0,07 |
5 |
|
|
|
|
10,8 |
8,72 |
9,51 |
11,15 |
0,07 |
4 |
|
|
|
|
11,0 |
9,20 |
9,72 |
11,27 |
0,07 |
0 |
|
|
|
|
11,0 |
9,34 |
9,81 |
11,36 |
0,07 |
9 |
|
|
|
|
У нашій моделі |
є три |
ендогенні |
змінні Y , R, I і |
дві |
екзогенні |
змінні |
M , G . |
|||
Ідентифікуємо кожне з рівнянь. |
|
|
|
H 2 , |
|
|
|
|||
Перше рівняння. Кількість залучених ендогенних |
змінних |
не |
залучено одну |
|||||||
екзогенну |
змінну |
G , тому |
D 1. Таким чином, |
H D 1, |
тобто |
рівняння |
строго |
|||
ідентифіковане. |
|
|
|
змінних H 2 , |
|
|
|
|||
Друге рівняння. |
Кількість |
залучених |
ендогенних |
не |
залучено одну |
|||||
екзогенну |
змінну |
M , тому |
D 1. Таким чином, |
H D 1, |
тобто |
рівняння |
строго |
|||
ідентифіковане. |
|
|
|
|
|
H 2 , |
|
|
|
|
Третє рівняння. |
Кількість |
залучених |
ендогенних |
змінних |
не |
залучено дві |
||||
екзогенні |
змінні |
M , G , тому D 2 . |
Таким чином, |
H D 1, |
тобто рівняння |
|||||
надідентифіковане.
Перевіримо для кожного рівняння достатню умову ідентифікації. Для цього складемо
матрицю коефіцієнтів при змінних моделі: |
|
|
|
|
|||
|
Y |
R |
I |
M |
G |
||
1 |
|
-1 |
0 |
|
2 |
0 |
|
рівняння |
|||||||
1 |
|
|
|
|
|||
2 |
-1 |
0 |
|
0 |
|
||
рівняння |
|||||||
|
|
1 |
|
|
2 |
||
3 |
0 |
|
-1 |
0 |
0 |
||
рівняння |
|||||||
|
1 |
|
|
|
|
||
Відповідно до достатньої умови ідентифікації визначник матриці коефіцієнтів при змінних, що не входять до досліджуваного рівняння, не має дорівнювати 0, а ранг матриці має дорівнювати кількості ендогенних змінних моделі мінус 1, тобто 3 – 1 = 2.
155

Перше рівняння. Матриця коефіцієнтів при змінних, що не входять до рівняння, має
вигляд |
A |
|
1 |
2 |
|
. Очевидно, що її ранг дорівнює 2, а |
det A |
det |
1 |
2 |
|
|
2 |
0 . |
||
|
1 |
|
|
1 |
0 |
|
|
1 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Достатня умова для першого рівняння виконується.
Друге рівняння. Матриця коефіцієнтів при змінних, що не входять до рівняння, має
вигляд A |
|
1 |
2 |
|
. Її ранг також дорівнює 2, а |
det A |
det |
1 |
2 |
|
|
|
0 . Достатня |
||
2 |
|
|
|
0 |
|
|
2 |
|
|
|
0 |
|
|
2 1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
умова для першого рівняння виконується.
Третє рівняння. Матриця коефіцієнтів при змінних, що не входять до рівняння, має
вигляд A |
|
1 |
2 |
0 |
|
. Її ранг дорівнює 2, оскільки визначник квадратної підматриці |
|
3 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
2 |
|
|
2 х 2 цієї матриці не дорівнює 0, а |
det A* |
det |
1 |
2 |
|
|
2 |
0 |
. Достатня умова для |
|
|
3 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
першого рівняння виконується.
Таким чином, перші два рівняння моделі строго ідентифіковані; щоб оцінити їх, застосуємо непрямий метод найменших квадратів, останнє рівняння надідентифіковане,
його оцінимо за допомогою двохетапного методу найменших квадратів. |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Перетворимо систему до зведеного вигляду. Підставляючи третє рівняння в друге, |
|||||||||||||||||||||||||||||||||
отриманий результат – у перше рівняння, неважко одержати систему |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rt 10 11Gt 12Mt v t , |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Yt 20 21Gt 22Mt |
v2t , |
|
|
|
|
(*) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
It 30 31Gt 32Mt v3t , |
|
|
|
|
|
|
|
|
||||||||||||
де |
|
|
|
|
0 1 0 1 1 0 |
; |
|
|
|
|
|
|
1 2 |
; |
|
|
|
|
2 |
|
; |
|
|
0 1 1 0 1 1 |
; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
10 |
|
|
1 1 1 1 |
11 |
|
1 |
1 1 1 |
12 |
|
1 1 1 1 |
20 |
|
|
1 1 1 1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 2 1 |
; |
22 |
|
|
|
2 1 |
; |
|
0 1 0 0 1 1 ; |
31 |
|
|
2 |
; |
|
|
2 1 1 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
21 |
|
1 1 1 1 |
|
|
1 |
1 1 1 |
30 |
|
|
|
|
1 1 1 1 |
|
|
|
1 1 1 1 |
12 |
|
1 1 1 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Застосування непрямого методу найменших квадратів вимагає знайти коефіцієнти системи в структурному вигляді через коефіцієнти tj ,t 1,3, j 0,2 . Неважко знайти
|
|
|
|
|
|
|
32 , |
22 |
, |
|
11 |
, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
32 |
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
21 |
|
|
|
|
|
|||||||
|
|
|
|
21 |
1 |
|
|
|
12 21 11 22 |
, |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|
|
1 1 1 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
1 |
|
|
12 21 11 22 |
. |
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
12 |
|
1 1 1 |
|
|
|
|
|
21 |
|
|
|
|
|
|
|||||||
Розв'язуючи систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 , |
||||||||||||||
|
|
|
|
|
0 |
|
|||||||||||||||||||||
|
|
|
|
0 |
|
|
1 0 |
1 1 |
|
|
|
10 |
|
|
1 1 1 |
|
|
|
|
||||||||
|
|
|
0 1 1 0 1 0 20 1 1 1 1 , |
||||||||||||||||||||||||
|
|
|
|
|
|
1 0 1 0 30 1 1 1 1 , |
|||||||||||||||||||||
|
|
|
0 1 |
||||||||||||||||||||||||
отримуємо |
|
|
10 21 11 20 |
|
|
|
|
20 32 22 30 |
|
|
|
|
|
30 12 32 10 |
|
||||||||||||
|
0 |
|
, |
|
|
|
, |
0 |
|
. |
|||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
21 |
|
|
|
|
|
0 |
|
|
32 |
|
|
|
|
|
|
|
|
12 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Застосовуючи звичайний МНК, оцінимо рівняння системи (*):
Rˆ t 3,594 0,044Gt 0,279Mt , R2 0,75 ; Yˆt 1,302 0,917Gt 0,074Mt , R2 0,97 ; Iˆt 8,488 2,194Gt 0,329Mt , R2 0,80 .
156
