
Mech-Slobod
.pdf61
З визначення маси випливає спосіб її вимірювання (порівняння мас). До кожного з тіл, маси яких необхідно порівняти, прикладаємо одну й ту ж саму силу і вимірюємо прискорення, яких вони набувають під дією цієї сили. Відношення мас буде дорівнювати оберненому відношенню прискорень
m1 |
= |
a2 |
. |
(3.3) |
m |
|
|||
|
a |
|
||
2 |
1 |
|
|
|
Обравши деяке тіло за еталон маси, можна, в такий спосіб порівнювати масу будь-якого тіла з цим еталоном. Одиницею маси в системі СІ є кілограм, а первинним еталоном, що відтворює цю одиницю є спеціально створений прототип, що являє собою циліндр висотою та діаметром 39 мм,
виготовлений із сплаву платини (90%) та іридію (10%). Він постійно зберігається в Міжнародному бюро мір і вагів у Парижі.
Еталон кілограма – це єдиний з еталонів основних механічних одиниць (див. Табл. 1.1 у
Вступі), який не може бути відтворений природним шляхом, а потребує порівняння з прототипом,
хоча початкова ідея полягала в тому, що маса прототипу повинна співпадати із масою 1 дм3 води при її найбільшій густині (при температурі 3,98 С) і при тиску 1 фізична атмосфера (101 325 Па).
На перший погляд, такий еталон легко відтворити, але на практиці виникає цілий ряд серйозних проблем, починаючи від точного відтворення згаданих умов до коливань ізотопного складу води різного походження. Це спонукало вдатися до виготовлення спеціального еталону, який здатний забезпечити сталість визначення 1 кг з відносною точністю краще за 10-8 протягом багатьох тисяч років. Насправді виявилось, що маса прототипу більша за масу 1 дм3 води при згаданих умовах на
28 мкг. Взагалі, принципова можливість створення еталону одиниці маси, який можна відтворити будь-де, подібно до еталонів метра та секунди, існує, наприклад, як маси певної кількості атомів певного стабільного ізотопу певного хімічного елементу.
Оскільки маса визначається одним числом – відношенням модулів двох векторів, то вона є скалярною величиною. Підводячи підсумок можна сформулювати таке означення:
Маса – це скалярна фізична величина, що характеризує інерційні властивості тіл (є
мірою інертності тіл).
62
Ще раз підкреслимо, що тут йдеться про так звану інерційну масу. Вся сукупність дослідів і спостережень свідчить про те, що в рамках класичної механіки, тобто при швидкостях руху,
набагато менших за швидкість світла, маса має дві такі важливі властивості:
•Маса є величина адитивна, тобто маса складеного тіла дорівнює сумі мас його складових частин;
•Маса тіла є величина стала, що не змінюється при його русі.
На підставі узагальнення результатів дослідів (формули (3.1−3.3)) може бути сформульований другий закон Ньютона:
Прискорення частинки в інерціальній системі відліку прямо пропорційне прикладеній
до неї силі і обернено пропорційне її масі.
Другий закон Ньютона може бути виражений векторним рівнянням
G |
G |
|
|
|
|
|
|
(3.4) |
ma |
= F , |
|
|
|
|
|
|
|
де |
F e |
загальному |
випадку |
є результуюча |
(векторна сума) всіх сил, |
прикладених до |
||
|
|
G |
|
n |
G |
|
|
|
матеріальної |
точки, F |
= ∑Fi . |
Зауважимо, що |
при запису рівняння |
(3.4), коефіцієнт |
|||
i=1
пропорційності, про яку йдеться в наведеному вище означенні другого закону Ньютона, покладено рівним одиниці.
Рівняння (3.4) називають основним рівнянням динаміки матеріальної точки, оскільки воно дозволяє за відомою масою та відомими силами, прикладеними до частинки, визначити її прискорення, а потім, використовуючи початкові умови, також її швидкість та положення в будь-
який момент часу (див. 2.1.4), або, як прийнято говорити, її механічний стан.
Механічний стан частинки в кожний момент часу визначається її положенням та
швидкістю, тобто її радіус-вектором r (t) та вектором швидкості υ (t) .
Таким чином, рівняння (3.4) описує еволюцію механічного стану частинки з часом.
Рівняння, які описують часову еволюцію стану фізичної системи прийнято називати рівняннями руху. Отже рівняння (3.4) є рівняння руху частинки. За його допомогою при наявності необхідних даних може бути знайдено закон руху частинки у формі r = r (t) .
63
У частинному випадку вільного руху частинки, коли на частинку не діють ніякі сили, в рівнянні (3.4)
FG = 0 , звідки випливає, що a = 0 , а отже і υ = const , що відповідає прямолінійному рівномірному рухові.
Цей висновок співпадає за змістом із першим законом Ньютона, в зв’язку з чим може виникнути враження, що перший закон Ньютона є наслідком другого. Але, як ми бачили, саме перший закон постулює існування інерціальних систем відліку, а другий закон справедливий лише в таких системах відліку і тому перший закон формулюють незалежно від другого.
3.3. Фундаментальні взаємодії та сили актуальні в механіці
Оскільки сила в механіці є мірою взаємодії, то логічно класифікувати сили за відповідними взаємодіями. На сьогодні відомі чотири фундаментальні взаємодії, характеристики яких наведено в Таблиці 3.2. Хоча сильна взаємодія набагато інтенсивніша за інші, її радіус оцінюється лише як
10-13 м. Ще менший радіус слабкої взаємодії. Ці взаємодії відіграють вирішальну роль у фізиці атомного ядра та елементарних частинок, але в задачах класичної механіки, область застосування якої обмежується макроскопічними тілами, вони ніяк не проявляються внаслідок малого радіусу їх дії.
Таблиця 3.2
Фундаментальні взаємодії
|
Назва взаємодії |
Інтенсивність взаємодії |
|
Радіус взаємодії |
|
|
|
|
|
1. |
Сильна |
1 |
10-13 |
м |
2. |
Електромагнітна |
10-2 ÷ 10-3 |
∞ (F ~ 1/r2) |
|
3 Слабка |
10-12 |
10-18 |
м |
|
4. |
Гравітаційна |
10-39 ÷ 10-45 |
∞ (F ~ 1/r2) |
|
Таким чином у механіці актуальними є лише гравітаційна та електромагнітна взаємодії, і
відповідні сили.
3.3.1. Закони сил
Для того, щоб звести відшукання закону руху частинки до чисто математичної задачі,
необхідно знати так звані закони сил, або, як ще іноді кажуть, формули сил, прикладених до
64
частинки, тобто залежність сил від інших фізичних величин. Закони сил встановлюються експериментальним шляхом за допомогою розглянутих вище способів вимірювання сил.
Розглянемо закони сил, які застосовують при розв’язанні задач класичної механіки.
Сила гравітаційного притягання. Сила гравітаційного притягання, що діє між двома матеріальними точками, визначається законом всесвітнього тяжіння, встановленим Ньютоном, який виражається формулою
F = G m1m2 |
|
(3.5) |
|
|
r2 |
|
|
де |
G – так звана гравітаційна стала ( G = 6,67 10-11 н м2 кг−2 ); m та m |
2 |
– гравітаційні |
|
1 |
|
|
маси частинок, що взаємодіють; r – відстань між частинками. Гравітаційні маси, що фігурують в формулі закону всесвітнього тяжіння (3.5) встановлюють на основі цього закону і вони є мірою гравітаційних властивостей тіл, тобто їх здатності притягуватись одне до одного незалежно від їх інших фізичних властивостей. Про закон всесвітнього тяжіння (3.5) та гравітаційну масу докладно йтиметься в Розділі 8. Зараз ми лише зауважимо, що дослідним шляхом з високою точністю встановлено пропорційність інертної та гравітаційної мас. Це дозволяє вважати їх рівними, тобто для їх вимірювання вживати один і той же самий еталон (див. Табл. 1.1) Це дає можливість розширити визначення маси так:
Маса – це скалярна фізична величина, що є мірою інерційних та гравітаційних властивостей матерії.
У подальшому ми будемо використовувати термін маса без вказівок на її характер, за винятком випадків, коли таке уточнення необхідне.
Вектор сили гравітаційного притягання F12 , яка прикладена до частинки m1 з боку частинки
m2 у векторному вигляді можна записати так |
|
|
|
G |
|
||||
|
|
|
rG12 |
|
|
|
F12 |
|
|
FG |
= G m1m2 |
|
, |
(3.5а) |
m1 |
r12 |
m2 |
||
|
|
|
|||||||
12 |
r122 |
|
r12 |
|
G |
|
G |
|
|
|
|
|
|
|
|
r1 |
|
|
|
де |
початок |
|
радіус-вектора r12 , |
який |
|
|
r2 |
|
|
характеризує відносне положення частинок, обрано |
O |
|
Рис. 3.3. Гравітаційне притягання |
||
|
в місці розташування частинки m1 , а кінець – у
65
місці розташування частинки m2 . Відповідно напрямок сили F12 співпадає з напрямком радіус-
вектора rG12 (Рис. 3.3).
Однорідна сила тяжіння. У багатьох задачах про рух тіла в обмеженій ділянці простору поблизу поверхні Землі, вважають, що на тіло діє однорідна сила тяжіння
FG |
|
= mgG |
, |
(3.6), |
тяж |
|
|
|
|
де |
g – так званий вектор прискорення вільного падіння, направлений по лінії виска в даній |
|||
точці земної поверхні. (Докладніше про однорідну силу тяжіння йтиметься в Розділі 4).
Сила електромагнітної взаємодії. До електрично зарядженої частинки, що знаходиться в
електромагнітному полі, з боку цього поля прикладена сила |
|
F = qE + q[υG× B] , |
(3.7) |
де q – заряд частинки, υG – швидкість частинки, а E |
і B , відповідно – вектори |
напруженості електричного поля та індукції магнітного поля в місці знаходження частинки,
визначені в тій самій системі відліку, що й |
B |
|
B |
|
|
швидкість частинки υG . |
|
|
Силу, прикладену до частинки з боку |
|
F Лор |
магнітного поля FЛор = q[υG× B] ], називають |
υ |
υ |
F Лор |
q>0 |
q<0 |
силою Лоренца. Вона завжди направлена |
|
|
|
|
|
перпендикулярно Її знак змінюється на |
Рис. 3.4. Сила Лоренца |
|
|
|
|
протилежний при зміні знаку заряду |
|
|
Якщо електричне поле, що діє на заряджену частинку (точковий заряд ) q1 створюється
іншим точковим зарядом q2 , то сила взаємодії між ними, яку називають кулонівською силою,
визначається законом Кулона
F = k |
q1q2 |
, |
(3.8) |
|
r 2 |
||||
|
|
|
де r – відстань між ними, k – коефіцієнт пропорційності, що залежить від вибору системи одиниць2. Формули гравітаційної та кулонівської сил цілком подібні, але на відміну від маси m ,
2 У системі СІ, в якій одиницею електричного заряду є кулон, k = 1/ 4πε 0 = 8,8542 ×10−12 фарад/ метр.

66
яка є додатно визначеною величиною, величини електричних зарядів q можуть бути як
додатними, так і від’ємними, причому між зарядами одного знаку має місце відштовхування, а між зарядами різних знаків – притягання.
Кулонівську силу F12 , яка прикладена до точкового заряду q1 з боку точкового заряду q2 , у
векторному вигляді можна записати так
G |
|
|
q1q2 |
|
rG12 |
|
|
q1 |
G |
q2 |
F12 |
= −k |
r2 |
|
r |
, |
(3.8а) |
F12 |
r12 |
|
|
|
rG |
|
12 |
12 |
|
|
|
|
|
|
де |
– |
радіус-вектор, |
початок якого |
|
|
|
||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|
G |
G |
|
обрано |
в місці розташування точкового |
r1 |
r |
|
2 |
||||
заряду |
q1 , а кінець – у місці розташування |
O |
|
|
Рис. 3.5 Кулонівська сила відштовхування |
||||
|
|
|||
точкового заряду q2 . Якщо взаємодіють
заряди різних знаків, тобто коли q1q2 > 0 , то має місце притягання і напрямок силиFG12 співпадає з
напрямом радіус-вектора r12 . Якщо взаємодіють заряди одного знаку, тобто коли q1q2 < 0 , то має
місце відштовхування і напрямок силиF12 є протилежний напряму радіус-вектора rG12 (Рис. 3.5).
Формули сил, що виникають при механічному контакті тіл. У принципі, всі взаємодії тіл, рух яких розглядається в класичній механіці, можуть бути зведені до двох фундаментальних взаємодій: гравітаційної та електромагнітної. Але в такому випадку аналіз цілого ряду явищ виявився б настільки складним, що його практично не можна було б здійснити. Візьмемо для прикладу безпосередній механічний контакт двох тіл. На мікроскопічному рівні, тобто між атомами та молекулами цих тіл діють електромагнітні сили, які зумовлюють сили взаємодії між тілами, що проявляються макроскопічно, наприклад як деформація цих тіл. Але розрахувати ці макроскопічні сили шляхом врахування електромагнітної взаємодії нескінченного числа атомів неможливо. В таких випадках зручно ввести наближені закони сил, які встановлюють емпіричним шляхом і за допомогою яких з достатньою точністю кількісно описують реально існуючі на макроскопічному рівні взаємодії тіл.
При деформації твердих тіл відбувається зміщення частинок з положень рівноваги і на кожну частинку деформованого тіла діє сила, направлена до відповідного положення рівноваги,

67
яку при малих зміщеннях можна вважати пропорційною величині зміщення. Цю силу називають
силою пружної деформації або пружною силою (силою пружності)
Fпружн = −krG, |
(3.9) |
де r є вектор зміщення з положення рівноваги, а коефіцієнт k |
називається коефіцієнтом |
пружності.
Взагалі будь-яку силу, яку можна описати формулою (3.9), навіть не пов’язану з деформацією, називають квазіпружною силою3
Нехай два тверді тіла A і B дотикаються одне до одного (мають механічний контакт) у
точці K (Рис. 3.6). Силу R , з якою одне тіло (наприклад, A ) діє на інше тіло
(наприклад, B ) завжди можна розкласти на дві лінійно незалежні складові. Одна з них,
NG , перпендикулярна до дотичної площини
Q в точці контакту (на Рис. 3.6 слід
площини Q показано штриховою лінією) і
називається нормальною складовою сили
B NG
Q  RG
RG
A K 
FGтертя
Рис. 3.6. Сили при контакті двох тіл
реакції R або силою нормального тиску з боку тіла A на тіло B . Тангенціальна складова сили R
дістала назву |
сили |
тертя Fтертя . У |
|
|
|||||
випадку, коли має місце відносний рух |
F тертя |
|
|||||||
поверхонь, що дотикаються, тобто |
|
|
|||||||
ковзання, |
то |
силу |
Fтертя називають |
Сухе тертя |
|
||||
силою тертя ковзання або силою |
|
|
|||||||
зовнішнього тертя |
|
|
Рідинне тертя |
|
|||||
Gковз |
|
|
|
|
|
υG |
|
|
|
|
|
|
|
|
, |
О |
υ(3.10) |
||
Fтертя = −kN |
υ |
||||||||
|
|
|
|
|
|
|
Рис. 3.7. Залежність сил сухого та рідинного тертя |
від |
|
|
|
|
|
|
|
|
|
||
де |
N = |
|
N |
|
|
– модуль сили |
швидкості υ . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
3 Префікс квазі має грецьке походження і означає подібний.

68
нормального тиску, υG – відносна швидкість цих поверхонь, k – коефіцієнт тертя ковзання, який залежить від природи та стану поверхонь, що ковзають. Звичайно вважають, що коефіцієнт тертя ковзання для даної пари матеріалів є сталим і не залежить від швидкості υ , але експеримент показує, що така залежність існує, а, отже, існують, як правило, незначні відхилення від закону тертя (3.10). Типову залежність сили тертя ковзання від швидкості показано на Рис. 3.7. Вона звичайно зумовлена зміною стану поверхонь, що контактують у процесі руху. Вивчення механізмів тертя виходить за рамки курсу механіки і є предметом ряду спеціальних фізико-
технічних дисциплін.
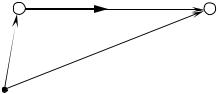
Якщо відносний рух поверхонь, що знаходяться в контакті, відсутній, то говорять про силу
тертя спокою Fтертяспок . Дійсно, коли ми прикладаємо до якого-небудь тіла з масою m , наприклад,
до шафи або парти, що перебуває у спокої на підлозі кімнати, зовнішню силу F зовн у
горизонтальному напрямку з метою пересунути його по підлозі, то рух починається не одразу4:
якщо величина прикладеної нами сили недостатня, то тіло залишається в спокої. З того факту, що прискорення тіла при цьому дорівнює нулю, випливає, що рівнодіюча всіх сил, прикладених до
тіла, дорівнює нулю: отже прикладена нами зовнішня сила F зовн зрівноважується іншими силами,
прикладеними до тіла відповідно до рівняння руху
0 = mgG + R + F зовн , |
(3.11) |
де mg – сила тяжіння, аR – сила реакції з боку підлоги. Оскільки сила тяжіння mg не має
горизонтальної складової, то вона не може зрівноважувати зовнішню силу F зовн . Остання може
врівноважуватись лише горизонтальною складовою сили реакції R , яку і називають силою тертя
спокою Fтертяспок (Рис. 3.8). Рівняння (3.11) можна переписати у вигляді
0 = mgG + N + F спок |
+ F зовн . |
(3.11а) |
тертя |
|
|
4Строго кажучи, макроскопічно помітний відносний рух поверхонь, що знаходяться в контакті, починається не одразу: спочатку має місце деформація (при малих навантаженнях оборотна) обох тіл, у першу чергу мікроскопічні деформації поблизу площини контакту.

69
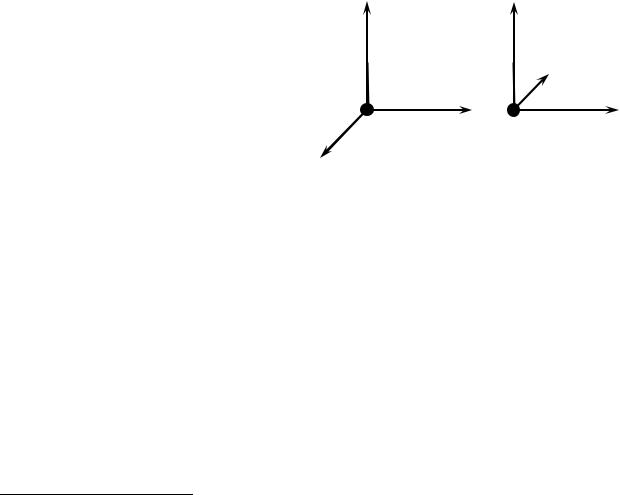
Оскільки взаємно перпендикулярні вектори є лінійно незалежні, то останнє рівняння еквівалентне двом векторним рівнянням, записаним окремо для горизонтальних та вертикальних складових
0 = F спок |
+ F зовн |
(3.12а) |
N |
тертя |
|
|
|
та |
|
F тертя |
F зовн |
|
|
|
|
0 = mgG + N . |
(3.12б) |
|
|
Із рівняння (3.12а) однозначно випливає, що доти, поки тіло знаходиться в спокої, сила тертя
спокою Fтертяспок є рівною за модулем і
F тертя
направленою протилежно силі F зовн (у
загальному випадку рівною за модулем і направленою протилежно сумі тангенціальних складових усіх інших сил,
прикладених до тіла). Таким чином, при
О
mg
Рис. 3.8. До поняття сили тертя спокою
А тертя ковзання
тертя спокою
F зовн
збільшенні сили F зовн зростає і сила |
Рис. 3.9. До поняття сил тертя спокою і ковзання |
|
|
F спок |
(ділянка OA на Рис. 3.9), а після початку руху переходить у силу тертя ковзання F ковз |
. При |
|
тертя |
|
тертя |
|
цьому модуль сили тертя спокою досягає своєї максимальної величини, що дорівняю модулю сили тертя ковзання, який в ідеалізованому випадку є сталим (горизонтальна штрихова лінія на Рис. 3.9).
Насправді така рівність має місце лише на початку руху, а потім модуль сили тертя ковзання може змінюватися в силу причин, що обговорювалися вище.
При поступальному русі тіла в рідині або в газі виникає сила, прикладена до тіла в напрямку,
протилежному швидкості тіла υG відносно рідини або газу, яку називають силою опору
середовища. При малих швидкостях величина цієї сили пропорційна швидкості. Отже формули сили опору:
FG |
= −kυG , |
(3.13) |
оп |
|
|
де коефіцієнт k |
називається коефіцієнтом опору і залежить як від форми і розмірів тіла, так |
|
і від характеристик рідини або газу.
70
Реальна залежність величини сили опору від швидкості є нелінійна. (Рис. 3.7). Цю нелінійність у формулі сили опору можна врахувати або введенням залежного від швидкості коефіцієнту опору k(υ ) або безпосереднім врахуванням наступних ступенів швидкості.
Наприклад, в аеродинаміці використовують формулу
FG = −kυ 2 υ |
(3.14) |
оп υ
Силу опору FGоп = −kυG часто називають силою внутрішнього тертя. Походження цього
терміну пов’язано з тим, що у переважній більшості випадків найближчий до тіла шар рідини рухається разом із тілом і вже цей шар має відмінну від нуля швидкість щодо наступного шару рідини внаслідок чого сила опору фактично виникає не безпосередньо між пластиною і рідиною, а
між сусідніми шарами рідини, що рухаються з різною швидкістю. Внутрішнє тертя в рідинах називають також рідинним тертям на відміну від сухого або зовнішнього тертя, що має місце безпосередньо між поверхнями твердих тіл. Використання нами для позначення коефіцієнтів пружності, тертя та опору різних за своєю природою однієї й тієї ж самої букви k , як це найчастіше робиться в літературі, не повинно призводити до непорозумінь. Там, де необхідно, ми будемо вживати додаткові індекси.
Спільною рисою всіх сил тертя (за винятком сили тертя спокою) та опору незалежно від конкретного механізму їх виникнення є те, що вони завжди направлені протилежно вектору відносної швидкості, тобто протилежно до напряму руху.
Утой же час між рідинним і сухим тертям існує суттєва відмінність, яка полягає в тому, що
врідині відсутня сила тертя спокою: рух одного шару рідини відносно іншого може початись під дією наскільки завгодно малої сили. Це добре відомо з повсякденної практики: людина може легко зрушити з місця навантажений човен або навіть невеликий катер, що плаває на воді, хоча про ту саму операцію на суходолі не може бути й мови. Для зменшення сили тертя між рухомими частинами різних механізмів зовнішнє (сухе) тертя між поверхнями замінюють внутрішнім
(рідинним) тертям шляхом змащування цих поверхонь різноманітними мастилами. При змащуванні між поверхнями твердих тіл існує тонкий шар рідини (оливи, мастила) і в ідеальному випадку ці поверхні втрачають безпосередній контакт між собою, а лише захоплюють прилеглі шари рідини, які потім “труться” між собою.
