
Вища Математика для Економістів
.pdf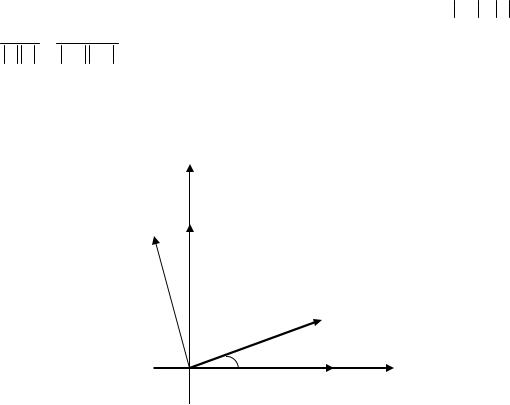
Ортогональні перетворення
Лінійне перетворення y = Qx називається ортогональним, якщо матриця Q є ортогональною. Ортогональне перетворення має таку властивість: для будь-яких двох векторів їх скалярний добуток дорівнює скалярному добутку їх образів при цьому перетворенні.
Дійсно, нехай u,v En , тоді Qu T Qv uT QT Qv = uT v .
Звідси випливає, що при ортогональному перетворенні довжини векторів та кути між ними не змінюються, бо Qu = u і
u,v = Qu,Qv . u v Qu Qv
Розглянемо такі ортогональні перетворення, як обертання і відбиття.
Нехай на площині x1Ox2 кожний радіус-вектор x замінюється радіус-вектором y , який одержаний в результаті обертання x на кутпроти годинникової стрілки (рис. 2).
x2
e2 e2
e1
φ
e1 x1
Рис. 2.
Визначимо матрицю перетворення обертання в
натуральному базисі, який складається з ортонормованих векторів
e1 1 0 T , e2 0 1 T . |
У результаті вказаного перетворення |
|
базисний вектор e1 замінюється вектором |
|
|
e1 cos e1 sin e2 , а |
||
базисний вектор e2 - |
вектором e2 sin e1 |
cos e2 . Тоді матриця |
перетворення обертання має вигляд: |
|
|
|
|
132 |
cos |
sin |
(39) |
T |
. |
|
sin |
cos |
|
Перетворення обертання в просторі Rn визначається матрицею обертання Tij , яка відрізняється від одиничної матриці лише чотирма елементами, розміщеними на перетині рядків і стовпців з
номерами |
i та |
j |
i j , |
|
причому |
два діагональних |
елементи |
||||||||||
дорівнюють cos , а два інших дорівнюють sin та sin . |
|
||||||||||||||||
|
|
Перетворенню |
відбиття відповідає матриця відбиття |
||||||||||||||
(матриця Хаусхолдера) |
H = E - 2uuT , |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
(40) |
||||||||
де u - нормований вектор |
|
|
u |
|
1 . Зауважимо, |
що матриця H є |
|||||||||||
|
|
||||||||||||||||
симетричною, |
бо |
HT E - 2uuT T |
ET 2 uT |
T |
uT E - 2uuT H . |
||||||||||||
Покажемо, |
що |
матриця H |
|
|
|
є ортогональною. |
|
Дійсно, |
оскільки |
||||||||
uT u |
|
u |
|
2 1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
HT H E - 2uuT 2 |
|
|
E 4uuT 4uuT uuT E . |
|
||||||||
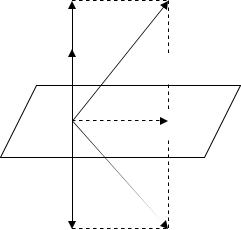
З’ясуємо геометричний зміст відбиття в просторі R3 . Здійснимо
відбиття відносно деякої площини V , що проходить через початок координат. Нехай u - одиничний вектор, який ортогональний до будь-якого вектора площини. Візьмемо довільний вектор x R3 і
розкладемо його на дві складові: паралельну до u , тобто xu u uT x ;
перпендикулярну до u , тобто проекцію на площину V , яка визначається рівністю
xv x xu x u uT x E uuT x . |
(41) |
|
При відбитті вектора x відносно площини |
V його |
|
перпендикулярна складова xv |
залишається незмінною, а паралельна |
|
складова xu змінює знак |
(рис. 3), тому відбитий |
вектор z |
визначається як |
|
|
z x 2xu E 2uuT x Hx . |
|
|
133
xu x
u
 xv
xv
-xu |
z |
|
|
Рис. 3. |
|
Отже, ми маємо справу з перетворенням відбиття. |
|
|
Дві множини U і V |
евклідова простору |
називаються |
ортогональними U V , якщо кожний вектор з U |
ортогональний |
|
до кожного вектора з V .
Множина всіх векторів, ортогональних до множини U ,
називається ортогональним |
доповненням |
|
множини |
U |
і |
|||||||
позначається через U . |
|
|
|
|
|
|
|
|
|
|||
Зауважимо, |
|
що |
U |
є |
підпростором |
евклідова |
простору |
|||||
незалежно від того, чи є U підпростором. |
|
|
|
|
|
|
||||||
Теорема. |
Якщо |
U - |
підпростір евклідова |
простору |
En , то |
|||||||
En U U та U |
|
U . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
Ядром m n -матриці |
A називається множина |
N A |
векторів |
|||||||||
x En , для яких Ax = 0 . |
|
|
|
|
|
|
R A |
|||||
Образом |
m n -матриці |
A називається |
множина |
|||||||||
векторів v Em , вигляду v = Au , де u - деякий вектор простору En . |
|
|||||||||||
Множини N A та R A |
є підпросторами вимірності n r A |
і |
||||||||||
r A відповідно, |
тобто |
dimN A n r A ; |
dimR A r A . |
|||||||||
Вимірність ядра матриці A називається дефектом матриці і |
||||||||||||
позначається через d A , отже, |
d A n r A . |
|
|
|
|
|
|
|||||
Теорема. |
Для |
будь-якої матриці A |
має |
місце |
рівність |
|||||||
N A R AT . |
|
|
|
|
|
|
|
|
|
|
|
|
134
Із сформульованої теореми випливає, що підпростір N A ,
утворений розв’язками системи |
Ax = 0 , |
є |
ортогональним |
||||||
доповненням до підпростору, натягнутому на рядки матриці A . |
|||||||||
Приклад |
19. |
Доповнити |
ортогональну |
систему |
векторів |
||||
e1 1 1 1 0 T , e2 2 0 2 |
1 T до ортогонального базису простору |
||||||||
E4 . |
|
|
|
|
|
|
|
|
|
Знаходимо |
вектор e3 |
x1 |
x2 |
x3 x4 T |
з умов |
ортогональності |
|||
e1T e3 0, eT2 e3 0 . |
Ці |
умови |
представляють |
собою |
систему |
рівнянь |
|||
відносно координат вектора e3 : |
|
|
|
|
|
|
|||
|
|
x1 x2 x3 |
0, |
|
|
|
|
||
|
|
|
2x3 |
x4 0. |
|
|
|
|
|
|
|
2x1 |
|
|
|
|
|||
Фундаментальну систему розв’язків цієї системи складають вектори
a1 1 1 0 |
2 T , a2 |
0 1 |
1 2 T . |
За вектор e3 |
візьмемо один з |
||||||
цих векторів, наприклад a1 . |
|
|
|
|
|
|
|
|
|||
Вектор |
e4 y1 y2 y3 |
y4 T |
|
визначимо |
згідно |
умов |
|||||
e1T e4 0, eT2 e4 |
0, eT3 e4 |
0 . Відповідна система рівнянь має вигляд: |
|||||||||
|
|
y1 y2 y3 |
|
|
|
0, |
|
|
|||
|
|
|
|
|
2y3 |
|
y4 0, |
|
|
||
|
|
2y1 |
|
|
|
||||||
|
|
|
y y |
2 |
2y |
4 |
0. |
|
|
||
|
|
|
1 |
|
|
|
|
|
|
||
Фундаментальною системою розв’язків є вектор 1 3 2 2 T , який
ми візьмемо за e4 .
Приклад 20. Застосувавши процес ортогоналізації Грама-
Шмідта |
|
|
до |
|
системи |
векторів |
a1 1 1 |
0 T , a2 |
0 |
2 1 T , a3 |
2 |
2 3 T одержати |
ортогональну |
систему векторів b1, b2, b3 . |
|
|
|
|
|
|
|
|
|||||||
Покладемо b1 = a1 . Шукаємо вектор b2 |
у вигляді b2 a2 21b1 . |
||||||||||||||
Число |
21 |
визначаємо |
з |
|
умови |
bT2 b1 0 . |
Оскільки |
||||||||
0 bT2 b1 aT2 b1 21b1T b1 , то |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
aT2 b1 |
|
2 |
1, |
b |
|
a |
|
b 1 1 1 T . |
|
||
|
|
b1T b1 |
|
|
|
|
|||||||||
|
|
21 |
|
2 |
|
|
2 |
|
2 |
|
1 |
|
|
||
Тепер шукаємо вектор b3 |
у вигляді b3 a3 31b1 32b2 . Числа |
||||||||||||||
31 і 32 |
визначаємо з умов bT3 b1 |
0, bT3 b2 |
0. З урахуванням рівності |
||||||||||||
bT2 b1 0 |
маємо 0 bT3 b1 aT3 b1 31b1T b1, |
0 bT3 b2 aT3 b2 32bT2 b2 . |
|||||||||||||
Звідси випливає, що
135
|
|
|
aT3 b1 |
|
4 |
2, |
|
|
aT3 b2 |
|
3 |
1, |
b |
|
a |
|
2b b |
|
1 1 2 T . |
|
|
b1T b1 |
|
|
bT2 b2 |
|
|
|
|
||||||||||||
|
31 |
|
2 |
|
32 |
|
3 |
|
|
3 |
|
3 |
|
1 |
2 |
|
||||
|
|
Отже, |
b1 1 1 |
0 T , b2 1 1 |
1 T , b3 |
1 |
1 2 T . |
|||||||||||||
|
|
Приклад 21. Скласти рівняння гіперплощини, що проходить |
||||||||||||||||||
через точку |
A 2,3,1, 2 |
афінного простору S4 |
перпендикулярно до |
|||||||||||||||||
прямої x 1 3 |
2 4 2 T . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Якщо x0 |
- радіус-вектор точки A , то з рівняння гіперплощини |
|||||||||||||||||
aT x b , де вектор a |
є нормаллю до гіперплощини, випливає, що |
|||||||||||||||||||
aT x0 b . З цих рівностей знаходимо, |
що aT x x0 0 . Нормаллю до |
|||||||||||||||||||
гіперплощини є вектор, що утворює напрямний підпростір прямої,
тобто a 3 2 4 2 T . Підставивши координати векторів a, x, x0 у
рівняння гіперплощини, будемо мати:
3x1 2x2 4x3 2x4 20 .
Приклад 22. Скласти рівняння гіперплощини, що проходить через точку A 2,1,1 афінного простору S3 паралельно до прямих x 1 1 1 T 1 1 1 3 T , x 0 0 1 T 1 0 1 1 T .
Нехай aT x x0 0 - шукане рівняння гіперплощини, причому
x0 2 1 1 T . Координати вектора |
нормалі a a1 a2 |
a3 T |
знаходимо з |
умов ортогональності вектора a |
і векторів 1 1 |
3 T , |
0 1 1 T , які |
утворюють напрямні підпростори даних прямих. Ці умови мають вигляд:
a1 a2 3a3 0,
a2 a3 0.
Фундаментальна система розв’язків цієї системи рівнянь складається з вектора 2 1 1 T , який є шуканим вектором a . Отже, маємо
рівняння гіперплощини:
2x1 x2 x3 4 .
Приклад 23. Знайти ортогональне доповнення до підпростору,
який породжується векторами a1 2 1 1 T , a2 2 3 4 T .
Позначимо через U підпростір, що породжується векторами a1, a2 . Легко перевірити, що ці вектори є лінійно незалежними, тому
dimU 2 . Доповнимо систему векторів a1, a2 |
до базису простору E3 . |
|
Шукаємо вектор a3 x1 x2 |
x3 T з умов a1T a3 |
0, aT2 a3 0 . Ці умови |
мають вигляд: |
|
|
136

2x1 x2 |
x3 0, |
||
|
3x2 |
4x3 0. |
|
2x1 |
|||
Фундаментальна система розв’язків цієї системи рівнянь складається
звектора 1 6 4 T , який є шуканим вектором a3 . Отже,
ортогональним доповненням підпростору U є одновимірний підпростір U , який породжується вектором a3 1 6 4 T .
Приклад 24. За допомогою перетворення подібності з ортогональною матрицею діагоналізувати симетричну матрицю
|
2 |
0 |
2 |
|
|
A |
|
0 |
4 |
2 |
|
|
. |
||||
|
|
2 |
2 |
3 |
|
|
|
|
|||
Власними значеннями |
|
і |
відповідними ортонормованими |
||
власними векторами матриці A є
1 0, x1 |
|
1 |
2 1 2 T , 2 3, x |
2 |
|
1 |
2 2 1 T , |
|
|
||||||
|
3 |
|
|
3 |
|
||
1 T3 6, x3 3 1 2 2 .
Діагоналізуючою матрицею S є ортогональна матриця Q , стовпцями якої є вектори x1, x2, x3 :
|
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
|
|
||
|
|
|
|
S = Q |
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
2 2 |
. |
|
|
||||
|
|
|
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким чином, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A Sdiag 0, 3, 6 S 1 |
= Qdiag 0, 3, 6 QT |
|
||||||||||||||
1 |
2 |
2 1 0 |
|
|
0 |
0 2 |
1 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
2 2 |
|
0 |
|
|
3 |
0 |
|
2 |
2 |
1 . |
||
|
|
|
||||||||||||||
3 |
|
2 |
1 2 |
|
0 |
|
|
0 |
6 |
|
1 |
|
|
|
||
|
|
|
|
|
|
|
2 2 |
|
||||||||
Приклад 25. За допомогою перетворення подібності з ортогональною матрицею діагоналізувати симетричну матрицю
|
|
2 |
1 |
1 |
|
A |
|
1 |
2 |
|
|
|
1 . |
||||
|
|
1 |
1 |
2 |
|
|
|
|
|||
Власними значеннями і відповідними власними векторами матриці A є
1 0, x1 1 1 1 T , 2 3 3, x2 1 1 0 T , x3 1 0 1 T .
137
Вектор x1 ортогональний до векторів x2 і x3 , проте вектори x2 і x3
не є ортогональними. Ортогоналізуємо ці вектори за методом ГрамаШмідта, в результаті чого одержимо ортогональну систему векторів
b1 1 1 0 T , b2 |
1 2 |
1 2 |
|
1 T . |
|
За |
|
|
допомогою |
|
|
|
ортогональної |
||||||||||||||||||||||||||||||||||
системи векторів x1, b1, b2 |
складемо ортогональну матрицю Q : |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
6 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x1 |
|
|
|
b1 |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Q |
|
|
|
|
|
|
1 3 |
|
|
1 2 1 6 . |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
x1 |
|
|
|
b1 |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
0 |
|
|
|
|
2 |
6 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тоді маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||||||||||||||
3 |
2 |
|
6 |
0 0 |
0 |
3 |
|
3 |
3 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A 1 3 |
1 2 |
|
|
1 6 |
0 3 |
0 |
1 2 |
|
1 2 |
|
0 . |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
0 |
|
|
|
2 6 |
|
|
|
|
|
|
1 6 |
1 6 |
2 6 |
||||||||||||||||||||||||||||||||
1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Приклад 26. |
Знайти |
|
|
|
образ і |
ядро |
матриці |
|
ортогонального |
||||||||||||||||||||||||||||||||||||||
перетворення A в просторі E3 , що полягає у проектуванні векторів на площину y z 0 .
|
|
|
|
Позначимо нормаль до площини (гіперплощини) y z 0 через |
|||||||||||
n 0 |
|
1 1 T , тоді відповідний нормальний вектор визначається як |
|||||||||||||
u = |
|
n |
|
|
1 |
0 1 1 T . |
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
За формулою (41) маємо: |
Ax = x - uuT x . Застосуємо це |
||||||||||
перетворення проектування |
до векторів натурального базису |
||||||||||||||
e1, e2, e3 простору E3 . Одержимо: |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Ae1 = e1 - uuT e1 e1 1 0 0 T , |
|||||||
|
|
|
|
Ae2 = e2 - uuT e2 |
1 |
0 1 1 T , |
Ae3 = e3 - uuT e3 |
1 |
0 1 1 T . |
||||||
|
|
|
|
2 |
2 |
||||||||||
Отже, матриця ортогонального перетворення має вигляд: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
1 2 |
1 2 |
|
||
|
|
|
|
|
|
|
|
|
A |
. |
|||||
|
|
|
|
|
|
|
|
|
|
0 |
1 2 |
1 2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
Очевидно, що r A 2 , тому образ матриці A є двовимірним підпростором, натягнутим на вектори 1 0 0 T , 0 1 1 T . Ядро матриці A має вимірність d A 3 2 1 та породжується вектором нормалі до гіперплощини, а саме вектором n 0 1 1 T .
138
§5. Квадратичні форми і додатно визначені матриці
Квадратичною формою від змінних x1, x2, , xn називається многочлен відносно цих змінних, який вміщує тільки їх другі степені:
n n
f x1, x2, , xn aij xi x j xT Ax ,
|
|
i 1 j 1 |
|
де x x1, x2, , |
xn T , |
A - симетрична матриця aij |
aji , яка |
називається матрицею квадратичної форми.
Обмеження, внаслідок якого матриця A повинна бути симетричною, не є суттєвим, бо якщо матриця B несиметрична і квадратична форма серед інших вміщує доданки bij xi x j bji x j xi , то,
поклавши aij |
aji |
|
1 |
bij |
bji , будемо мати в квадратичній формі |
|
|||||
|
|
2 |
|
|
|
замість зазначених доданків один доданок 2aij xi x j , а матриця
квадратичної форми стане симетричною.
Квадратична форма називається додатно (невід’ємно, від’ємно, недодатно) визначеною, якщо для будь-якого ненульового
вектора |
x |
виконується |
нерівність |
xT Ax 0 xT Ax 0, xT Ax 0, xT Ax 0 . |
|
||
Додатно (невід’ємно, від’ємно, недодатно) визначеною
називається симетрична матриця, яка відповідає додатно (невід’ємно, від’ємно, недодатно) визначеній квадратичній формі.
Очевидно, що від’ємно (недодатно) визначені квадратичні форми отримуються з додатно (невід’ємно) визначених зміною знаку. Тому досить обмежитися розглядом додатно і невід’ємно визначених форм.
Сформулюємо найбільш уживані ознаки додатної визначеності матриці.
Теорема. Для того, щоб симетрична матриця A порядку n буда додатно визначеною, необхідно і достатньо, щоб виконувалась одна з умов:
1.xT Ax 0 для всіх ненульових векторів x ;
2.всі власні значення матриці A додатні;
3.всі провідні (кутові) мінори матриці A додатні (критерій Сільвестра);
4.всі провідні елементи (без переставлень рядків) додатні;
5.існує невироджена матриця W така, що A = WT W .
Зауважимо, що ознаки невід’ємної визначеності матриці відрізняються від сформульованих заміною знаків додатності на
139

невід’ємність та зняттям обмежень на переставлення рядків і невиродженість матриці W .
Ознаку від’ємної визначеності матриці дає критерій Сільвестра: для того, щоб симетрична матриця A порядку n буда від’ємно визначеною, необхідно і достатньо, щоб знаки провідних
мінорів чергувалися, починаючи з від’ємного. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Матрицю W , про яку йде мова в теоремі, можна знайти одним |
|||||||||||||||||||||||||||||||
із способів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
W diag |
|
|
, |
|
|
|
, ..., |
|
|
|
|
|
QT , |
де |
Q |
|
- ортогональна матриця, |
||||||||||||||
|
1 |
|
2 |
n |
||||||||||||||||||||||||||||
складена |
з |
ортонормованих |
|
власних |
векторів матриці A , що |
|||||||||||||||||||||||||||
відповідають власним значенням i , |
i |
1,n |
: |
|
|
|
|
|
|
|
||||||||||||||||||||||
2) |
W A1 2 |
Qdiag |
|
|
, |
|
|
, ..., |
|
|
QT ; |
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
2 |
n |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3) |
W diag |
|
|
, |
|
, ..., |
|
|
|
U , |
де |
U |
- множник |
LDU -розкладу |
||||||||||||||||||
d1 |
d2 |
|
dn |
|||||||||||||||||||||||||||||
матриці A , d1, d2, ..., dn |
- її провідні елементи ( L, U відповідно нижня |
|||||||||||||||||||||||||||||||
і |
верхня |
трикутні матриці |
з одиницями на |
головній діагоналі, |
||||||||||||||||||||||||||||
D diag d1, d2, ..., dn ). |
|
|
|
|
|
|
|
|
|
|
|
W diag |
|
|
|
|
|
|
U , |
|||||||||||||
|
Представлення |
A = WT W , |
де |
|
|
, |
|
, ..., |
|
|||||||||||||||||||||||
|
d1 |
d2 |
dn |
|||||||||||||||||||||||||||||
називається розкладом Холецького для додатно визначеної матриці
A .
Рангом квадратичної форми називається ранг її матриці.
При заміні змінних x = Cy квадратична форма f переходить у квадратичну форму від нових змінних y1, y2, , yn . Перетворення змінних називається невиродженим, якщо матриця C цього перетворення є невиродженою.
Канонічним виглядом квадратичної форми рангу r називається представлення її алгебраїчною сумою квадратів:
f y2 |
y2 |
... y2, |
|
|
|
|
|
|
0, i 1,r . |
(42) |
|||||
1 1 |
2 2 |
r r |
i |
|
|
|
|
Коефіцієнти i називаються канонічними коефіцієнтами. |
Рівність |
||||||
(42) можна переписати наступним чином: |
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
f jy2j |
, |
|
|
|
(43) |
j 1
де j - не всі ненульові (кількість ненульових коефіцієнтів дорівнює
рангу форми).
Теорема. Будь-яку квадратичну форму ортогональним перетворенням можна звести до канонічного вигляду.
140

Нехай Q - ортогональна матриця, тобто Q 1 QT , та Q складається з ортонормованих власних векторів, що відповідають власним значенням матриці квадратичної форми A , тому
A = QΛQT , Λ diag 1, 2, ..., n ,
де 1, 2, ..., n - власні значення матриці A . Тоді |
|
|
n |
f |
xT Ax xT QΛQT x yT Λy j y2j , |
|
j 1 |
де y y1 y2 ... yn T |
QT x . Отже, квадратична форма за допомогою |
ортогонального перетворення x = Qy зведена до канонічного вигляду. Зауважимо, що звести квадратичну форму до канонічного вигляду можна і так званим методом Лагранжа або методом
виділення повних квадратів.
Нехай квадратична форма зведена до канонічного вигляду (42), причому відмінні від нуля канонічні коефіцієнти занумеровані так,
що 1, 2, ..., p є |
додатними, а p 1, p 2, ..., r |
|
- від’ємними. За |
||||||||||||||||
допомогою невиродженого лінійного перетворення змінних |
|||||||||||||||||||
y |
|
s |
, ..., y |
|
|
sp |
, y |
|
|
sp 1 |
, ..., y |
|
|
s |
, |
||||
|
1 |
p |
|
|
p 1 |
|
|
r |
|
r |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
1 |
|
|
|
p |
|
|
|
p 1 |
|
|
|
r |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
yr 1 sr 1, ..., yn sn
Квадратичну форму можна звести до вигляду:
f s2 |
... s2 |
s2 |
... s2 |
, |
(44) |
1 |
p |
p 1 |
r |
|
|
який називається нормальним виглядом квадратичної форми.
Теорема (закон інерції квадратичних форм). Кількість доданків з додатними (від’ємними) коефіцієнтами в нормальному вигляді квадратичної форми не залежить від способу зведення форми до цього вигляду.
Приклад 27. Дослідити на додатну (невід’ємну) визначеність матриці
|
2 |
1 |
0 |
|
|
|
1 |
0 |
1 |
|
||
A |
|
|
2 1 |
|
, |
B |
|
0 |
1 0 |
|
||
1 |
|
|
. |
|||||||||
|
|
0 |
1 |
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
1 |
||||||
Матриця A додатно визначена на підставі таких міркувань: 1)
власні значення |
1 2, 2,3 |
2 |
2 |
є додатними; 2) провідні мінори |
det A1 2, det A2 |
3, det A3 det A 4 |
є додатними; 3) провідні |
||
елементи d1 2, d2 3 2, d3 |
4 3 |
є додатними. |
||
Матриця B невід’ємно визначена на підставі кожної з ознак: 1) власні значення 1 0, 2 1, 3 2 є невід’ємними; 2) провідні мінори
141
