02_03_розділи

E

де E – будь-яка числова множина на осі 0x (осі абсцис у даних побудовах, див.р.1), а інтеграл справа розуміється як інтеграл Лебега ([1, 4]).

На основі (2.17) як її частковий випадок, а також користуючись формулами (2.11) і (2.15), подамо через щільність розподілу ймовірність потрапляння значень неперервної випадкової величини у заданий інтервал [x₁, x₂) із діапазону Е (рис.2.6), в результаті отримавши

P {x₁ ≤ X(ω) < x₂} ≡ F(x₂) – F(x₁) =

x₂ x₁ x₂

= ∫ ƒ(x) dx – ∫ ƒ(x) dx = ∫ ƒ(x) dx . (2.18)

-∞ -∞ x₁

Згідно з формулою (2.18) ймовірність потрапляння значень випадкової величини у заданий інтервал [x₁, x₂) дорівнює площі криволінійної трапеції, яка обмежена кривою щільності розподілу, віссю абсцис і прямими x = x₁ і x = x₂ (див. рис.2.6).

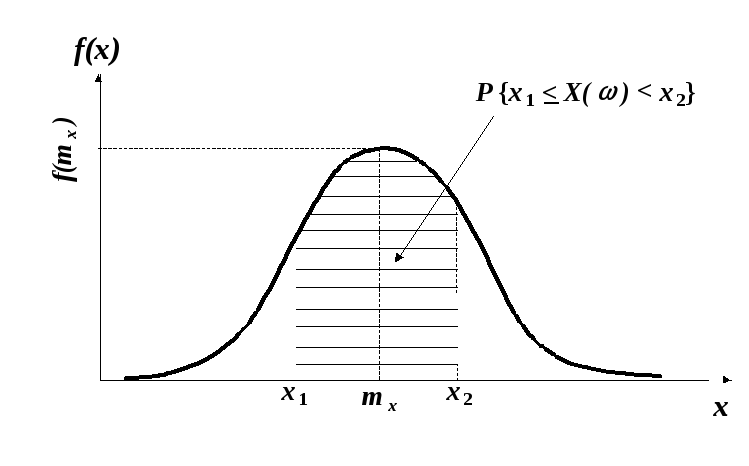
Рис.2.6 – Визначення ймовірності потрапляння значень неперервної випадкової величини у заданий інтервал (на прикладі графіка щільності розподілу рис.2.5)

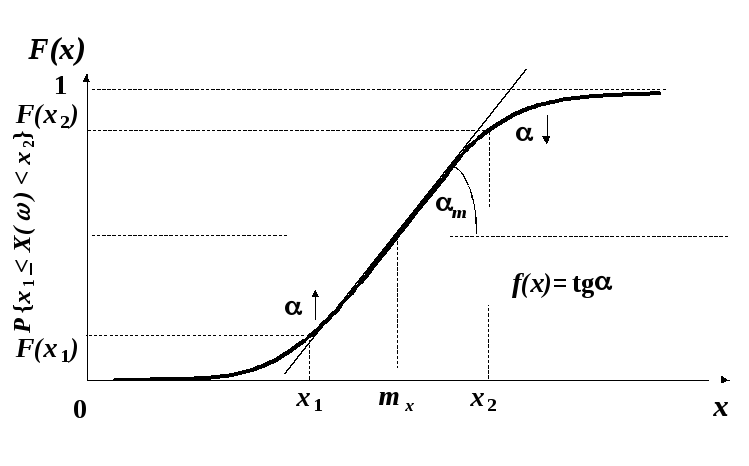
Рис.2.7 – Визначення ймовірності потрапляння значень неперервної випадкової величини у заданий інтервал (на прикладі графіка функції розподілу, що відповідає графіку щільності розподілу рис.2.6)

Використовуючи взаємозалежність щільності та функції розподілу неперервної випадкової величини {див. формули (2.13) і (2.15)} можна показати (див. рис.2.7), що нахил графіка функції розподілу F(x) характеризує значення щільності розподілу f(x) {f(x)=tg(α)}, при цьому чим більші значення щільності розподілу, тим швидше зростають значення F(x) (точка m_x на рис.2.7 з власною щільністю ймовірності характеризує т.зв. центр розподілу, див. наступний розділ).

Вважаючи у (2.18) x₁ = –∞ та x₂ = +∞, можна отримати

∞

P {–∞ < X(ω) < ∞} ≡ F(+∞) – F(–∞) = 1 – 0 = 1 = ∫ ƒ(x) dx , (2.19)

-∞

що характеризує, на додаток до невід'ємності власних значень, ще одну властивість щільності розподілу, а саме ту, що сумарна площа під графіком щільності розподілу на всьому діапазоні зміни х дорівнює одиниці (це стосується і діапазону [0, +∞), на доцільності дотримання якого при обробці географічних даних ми наголошували у вступі).

У підсумку повернемося ще раз до графіка щільності розподілу f(x) на рис.2.5. Візьмемо довільну точку х та елементарну ділянку dx, згідно з міркуваннями, вже наведеними у тексті між формулами (2.12) і (2.13), та зважаючи на (2.18). Величину ƒ(x) dx називають ще елементом ймовірності і саме цей елемент, як добуток щільності розподілу ймовірностей на довжину ділянки, з точністю до нескінченно малих величин найвищого порядку і визначає ймовірність потрапляння конкретного значення неперервної випадкової величини X(ω) на зазначену елементарну ділянку біля цього значення.

Виклавши у цьому розділі загальне поняття про закон розподілу випадкової величини, зазначимо, що розгляд теоретичних схем, аналітичних виразів і графічної інтерпретації основних теоретичних законів з огляду на можливості їхнього застосування для узагальнення та аналізу географічної інформації наведено у р.5.

Запитання та завдання до розділу 2 для самоконтролю

1.Яким чином можна цілком визначити дискретну випадкову величину?

2.Що таке закон розподілу випадкової величини у широкому розумінні?

3.У чому полягає відмінність емпіричного розподілу та теоретичного закону розподілу випадкової величини?

4.Що таке розподіл (ймовірностей) дискретної випадкової величини?

5.Якими є форми закону розподілу випадкової величини у точному розумінні?

6.Якою є відмінність двох різновидів інтегрального закону розподілу випадкової величини?

7.Сформулюйте властивості функцій розподілу F(x) і P_ex(x).

8.Поясніть зміст "стрибків" функції розподілу дискретної випадкової величини на графіку цієї функції.

9.Наведіть математичне та графічне тлумачення ймовірності потрапляння неперервної випадкової величини у заданий інтервал.

10.Що таке диференціальний закон розподілу неперервної випадкової величини?

11.Яким є взаємозв'язок між функцією розподілу та щільністю розподілу?

12.Чому дорівнює ймовірність того, що неперервна випадкова величина набере заданого конкретного значення?

13.Якими є властивості щільності розподілу?

14.Що характеризує нахил графіка функції розподілу? Поясність це графічно.

15.Що таке елемент ймовірності?

Проблемні теми для рефератів

1. Дві форми закону розподілу.

2. Зміст неперервного розподілу.

3. Типізація графіків розподілу.

Рекомендована література до розділу 2

1.Самойленко В.М. Ймовірнісні математичні методи в геоекології: Навчальний посібник (з грифом МОН України). – К.: Ніка-Центр, 2002. – С.54-68.

2.Самойленко В.М. Навчально-методичний комплекс з математично-модельного та геоінформаційного забезпечення підготовки географів. – К.: Ніка-Центр, 2003. – С.13-14, 25-26.

3.Самойленко В.М. Програма семінарсько-практичних занять з дисципліни "Математично-статистичні методи". – К.: Ніка-Центр, 2003. – С.5.

4.Казакевич Д.И. Основы теории случайных функций и ее применение в гидрометеорологии. – Л.: Гидрометеоиздат, 1977. – С.5-11.

3 Моменти розподілу випадкової величини

Закон розподілу ймовірностей значень випадкової величини у інтегральній і диференціальній формах, зміст якого був розглянутий у попередньому розділі, є звичайно, при заданих у р.2 умовах, вичерпною універсальною характеристикою цієї величини, але не єдиною. Остання теза пояснюється тим, що, по-перше, інтерпретація закону розподілу як певної графічної залежності (див. рис.2.1-2.5) очевидно передбачає необхідність відшукання загального аналітичного виразу цієї залежності. Такі вирази, як буде показано у р.5, істотно відрізняються для різних теоретичних схем, покладених в основу закономірностей розподілу різних випадкових величин, які відображають як єдність, так і певні фізичні особливості формування явищ і процесів у географії. Разом з тим, як відомо з курсу вищої математики, будь-яка графічна залежність може бути охарактеризована не тільки параметрами аналітичного виразу її функції, а й показниками, що відображають певні характерні (усереднені, екстремальні і т.ін.) точки такої функції тощо. Більше того, у імовірнісних методах усталено користуються не довільними, зазначеними останніми, числовими показниками, а визначеним їхнім набором, що зумовлює окремі суттєві риси розподілу ймовірностей значень випадкової величини. Саме до таких показників, насамперед і первісно, належать моменти розподілу випадкової величини різного порядку (надалі можливе вживання скороченого терміна "моменти випадкової величини" або просто "моменти розподілу"). Поняття моментів у математичній статистиці запозичене з механіки, де воно використовується для оцінювання розподілу мас (відомі "статичні моменти", "моменти інерції" тощо).

Застосування (крім законів) моментів розподілу як додаткової числової міри для вивчення випадкової величини пов'язане і з тим, що, по-друге, одними з вельми вагомих методично-прикладних завдань використання апарату імовірнісних методів для вивчення сукупностей фактографічних географічних даних загалом є оцінювання властивостей емпіричних розподілів цих даних і підбирання теоретичних законів розподілу, що найкраще відповідають їхній змінюваності (див. р.5). Вирішення вже таких завдань саме істотно і спрощується завдяки застосуванню моментів і, взаємопов'язаних з ними, узагальнювальних показників розподілу (див. далі р.4). Причім, за аналогією з вже розглянутими нами у попередньому розділі відмінностями між теоретичними законами розподілу та емпіричними розподілами, першим з них будуть відповідати власне моменти розподілу (інколи – "теоретичні" моменти розподілу), а другим – оцінки цих моментів або, іншими словами, вибіркові моменти розподілу ("емпіричні" моменти розподілу), визначені за обмеженою спостереженнями сукупністю фактографічних географічних значень випадкової величини, що вивчається.

Перейдемо до розгляду змісту загального поняття про моменти розподілу випадкової величини. Зрозуміло, що за такого спрямування будемо розглядати передусім "теоретичні" моменти (окремо для дискретної та неперервної випадкової величини), позаяк деталізації інших аспектів цього питання присвячено наступні розділи підручника.

Отже, довільні моменти розподілу дискретної випадкової величини {γ_k [X(ω)_д]} (γ – "гамма" мала) загалом визначаються за формулою

γ_k [X(ω)_д] = ∑ (x_i – a)^k p_i , (3.1)

i

де x_i – всі можливі значення дискретної випадкової величини X(ω)_д;

a – числова характеристика (довільна чи обрана певним чином точка на осі абсцис, яка може не збігатися або збігатися з нулем координат), від якої визначаються відхилення значень x_i;

p_i – ймовірності, відповідні x_i;

k – ступінь відхилень (порядок момента).

Зміст правої частини формули (3.1) стає більш зрозумілим, якщо зважити на положення, викладені у р.1 при розгляді поняття ймовірності x_i {формули (1.30)-(1.31)}, та на таку залежність для емпіричного аналога p_i – його відносної частоти або емпіричної забезпеченості ν_i, як

n n n

∑ (x_i – a)^k ν_i = ( ∑ (x_i – a)^k n_i ) / ∑ n_i = ( ∑ (x_i – a)^k n_i ) / n , (3.2)

i i=1 i=1 i=1

де n_i – абсолютні частоти кожного значення випадкової величини X(ω)_д або число (кількість) подій з x_i;

n – загальне число послідовно здійснених вимірів X(ω)_д у імовірнісному експерименті або його серіях. Зрозуміло, що для досягнення теоретичних схем розподілу та оперування з поняттям теоретичної ймовірності p_i має виконуватися залежність n → ∞ і при цьому n буде нескінченно наближатись до загального кількості всіх можливих елементарних наслідків експерименту ω, враховуючи і його серії, ν_i – до p_i {див. р.1 і формулу (1.31)}, а емпіричний момент за (3.2) – до теоретичного за (3.1).

Для неперервної випадкової величини, за її змістом, підсумовування за дискретними значеннями x_i у правій частині формули (3.1) слід замінити інтегруванням за всіма значеннями неперервного аргументу x, а ймовірності p_i – елементом ймовірності ƒ(x) dx, де ƒ(x) – щільність розподілу значень x неперервної випадкової величини X(ω). При цьому не слід забувати про прийняту у р.1 при усіх записах тотожність X(ω) = X(x) ≡ x.

Отже, згідно з засновками попереднього абзацу довільні моменти розподілу неперервної випадкової величини {γ_k [X(ω)]} k-го порядку визначаються за формулою

∞

γ_k [X(ω)] = ∫ (x – a)^k ƒ(x) dx . (3.3)

-∞

Графічна інтерпретація довільного момента будь-якої заданої фіксованої точки неперервного аргументу x у формулі (3.3) наведена на рис.3.1 на прикладі випадкової неперервної величини X(ω), що стосується всіх рисунків цього розділу. Така схема достатньо наочно ілюструє і формулу (3.1) для моментів дискретної величини, якщо замість графіка щільності розподілу, що є атрибутом неперервних розподілів, уявити собі ламану лінію графіка розподілу дискретної величини (наприклад, полігон розподілу, наведений на рис.2.1) із зрозумілою заміною на осі ординат ƒ(x) на p_i.

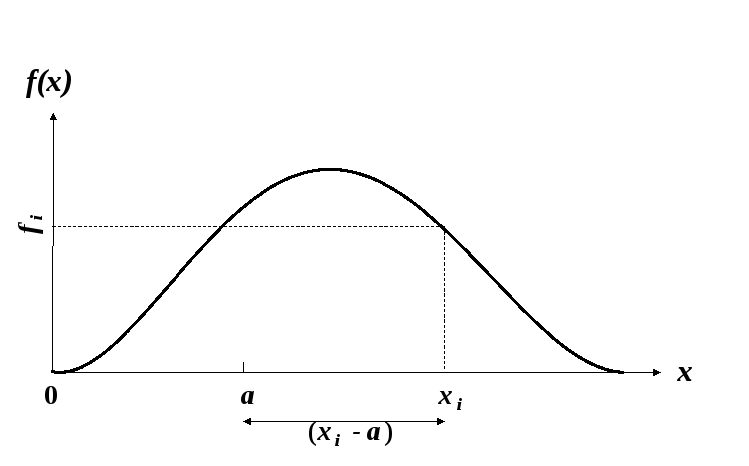
Рис.3.1 – Схема визначення довільного момента i-тої фіксованої точки x_i відносно a

У залежності від того, по відношенню до якої характеристики (точки) визначаються відхилення значень x_i при розрахунку моментів випадкової величини, крім довільних моментів {формули (3.1)-(3.3)} вирізняють також початкові (символ "m", загальний спрощений запис "m_k,x") і центральні (символ "μ", "мю" мала, загальний спрощений запис "μ_k,x") моменти певного (k-го) порядку. Перші з них визначають відносно осі ординат (a = 0) графіка щільності розподілу, а другі – відносно осі, що проходить через центр тяжіння цього графіка, який називають центром розподілу (див. детальніше р.4). Числова величина ординати точки останнього (до перетину з графіком щільності) теж маркує певну щільність ймовірності, а числове значення точки центру розподілу на осі x називають імовірнісним середнім або математичним очікуванням випадкової величини X(ω). Це математичне очікування, у свою чергу, є певним початковим моментом. Розглянемо зміст щойно викладених понять більш детальніше, зважаючи на те, що у прикладних завданнях цього підручника використовуються саме початкові та центральні моменти.

Примітка. Як показник центра розподілу (або центра групування) для різних завдань імовірнісного матаналізу та різних схем розподілу можна у цілому додатково використовувати не тільки математичне очікування, а й інші показники, розглянуті у р.4 (медіану, моду) при домінанті за значущістю математичного очікування. Крім того, для різних розподілів змістовне поєднання їхнього центра саме з математичним очікуванням не означає, що ордината (щільність ймовірності) останнього (див. для прикладу наступні рисунки) є обов'язково максимальною (див. р.5).

Отже, загальні формули визначення початкових моментів k-го порядку випадкової величини мають вигляд (рис.3.2):

• для дискретної випадкової величини

m_k [X(ω)_д] = ∑ x_i^k p_i , (3.4)

i

• для неперервної випадкової величини

∞

m_k [X(ω)] = ∫ x^k ƒ(x) dx . (3.5)

-∞

Рис.3.2 – Схема визначення початкового момента i-тої фіксованої точки x_i та числового значення математичного очікування (імовірнісного середнього, m_x) як першого початкового момента та щільності ймовірності цього середнього {f(m_x)}

Отже, початковий момент випадкової величини першого порядку m₁ [X(ω)] (інколи скорочено, перший початковий момент, див. рис.3.2) називають математичним очікуванням (імовірнісним середнім) випадкової величини X(ω) і позначають як математичний оператор (тобто відповідно до способів її розрахунку як числової характеристики, а не функції, значень випадкової величини, причім всіх значень, чому відповідають квадратні дужки) – Μ [X(ω)], розрізняючи дискретні та неперервні величини, а як конкретне числове значення (величину) – m_x.

Математичне очікування дискретної випадкової величини безпосередньо визначають як

M [X(ω)_д] = ∑ x_i p_i ≡ m_x , (3.6)

i

а неперервної випадкової величини як

∞

M [X(ω)] = ∫ x ƒ(x) dx ≡ m_x , (3.7)

-∞

або, зважаючи на взаємозалежність щільності та функції розподілу неперервної випадкової величини (див. р.2), як

∞

M [X(ω)] = ∫ x dF(x) ≡ m_x , (3.8)

-∞

де F(x) – функція розподілу (ймовірності неперевищення) випадкової величини (див. р.2), а інтеграл справа є т.зв. інтегралом Стілт'єса ([1, 4]), який розраховується як границя інтегральних сум.

Поняття математичного очікування (імовірнісного середнього) має велике вихідне методичне значення та грає особливу роль при застосуванні імовірнісних методів у географії, що буде доведено далі. Крім того, у р.4 і р.7 розглянуто певні важливі властивості математичного очікування довільної випадкової величини та систем таких величин, до того ж у р.4 – деякі властивості середнього арифметичного як "емпіричного аналога" імовірнісного середнього. У цьому ж розділі слід зазначити, що по-перше, якщо випадкова величина є невід'ємною, то і її математичне очікування є обов'язково невід'ємним.

По-друге, наприклад, зважаючи на формули (3.6)-(3.8) і зміст математичного очікування та на формули (3.4)-(3.5), неважко побачити, що початкові моменти k-го порядку випадкової величини можна подати через оператор M як імовірнісне середнє (математичне очікування) k-того ступеня довільної випадкової величини, тобто

m_k [X(ω)] = M [X(ω)^k] . (3.9)

Подання, аналогічні за змістом щойно розглянутому, будуть широко використані у всьому підручнику.

До розгляду змісту центральних моментів випадкової величини слід визначитись і з певним поняттям про перетворені випадкові величини. Так, зцентрована випадкова величина {X_зц(ω)} – це відхилення значень довільної випадкової величини X(ω) від її математичного очікування, причім імовірнісне середнє вже зцентрованої випадкової величини дорівнює нулю (доведення наведено далі за текстом), тобто

X_зц(ω) = X(ω) – m_x , (3.10)

M [X_зц(ω)] ≡ m_x,зц = 0 . (3.11)

Застосування зцентрованої випадкової величини призводить до того, що (рис.3.3) нуль координат графіка щільності розподілу зцентрованої величини збігається з нульовим числовим значенням математичного очікування цієї випадкової величини, а зцентровані (вже додатні та від'ємні) довільні значення останньої розташовуються по обидва боки від осі, що проходить через зазначене нульове значення математичного очікування. Таке своєрідне "зміщення" нуля координат при центруванні випадкової величини наведено на рис.3.3.

Рис.3.3 – Графік щільності розподілу зцентрованої випадкової величини та схема визначення центрального момента i-тої фіксованої точки x_i,зц

Зважаючи на щойно наведені положення та зміст рис.3.3, у цілому центральні моменти k-го порядку довільної випадкової величини {μ_k [X(ω)]} як її відхилення від власного центра розподілу (математичного очікування) можна означити як початкові моменти k-го порядку зцентрованої випадкової величини X_зц(ω) або як імовірнісне середнє (математичне очікування) k-того ступеня цієї X_зц(ω), тобто

μ_k [X(ω)] = m_k [X_зц(ω)] = M [X_зц(ω)^k] = M [(X(ω) – m_x)^k] . (3.12)

Тоді центральні моменти дискретної випадкової величини k-го порядку визначаться як

μ_k [X(ω)_д] = ∑ (x_i – m_x)^k p_i , (3.13)

i

а центральні моменти неперервної випадкової величини k-го порядку – як

∞

μ_k [X(ω)] = ∫ (x – m_x)^k ƒ(x) dx . (3.14)

-∞

Очевидно, що всі довільні моменти розподілу випадкової величини нульового порядку дорівнюють одиниці. А от центральний момент першого порядку цієї довільної величини (або імовірнісне середнє зцентрованої випадкової величини, про що вже йшла мова) завжди дорівнює нулю. Доведемо це, що рівносильне доведенню і формули (3.11).

Дійсно, для неперервної випадкової величини

∞

μ₁ [X(ω)] = M [X(ω) – m_x] = ∫ (x – m_x) ƒ(x) dx =

-∞

∞ ∞

= ∫ x ƒ(x) dx – m_x ∫ ƒ(x) dx = m_x – m_x = 0 . (3.15)

-∞ -∞

Для дискретної випадкової величини

μ₁ [X(ω)_д] = ∑ (x_i – m_x) p_i = ∑ x_i p_i – m_x ∑ p_i = m_x – m_x = 0 . (3.16)

i i i

Особливе місце при імовірнісному аналізі розподілу випадкової величини належить і центральному моменту другого порядку, який зветься дисперсією випадкової величини та позначається D [X(ω)] як математичний оператор (відповідно до способів його розрахунку як числової характеристики) або D_x як певне числове значення (величина). Згідно зі змістом центральних моментів дисперсією є імовірнісне середнє квадрата відхилення випадкової величини від її математичного очікування (див. рис.3.3), тобто

D [X(ω)] = μ₂ [X(ω)] = M [(X(ω) – m_x)²] ≡ D_x . (3.17)

Для дискретної випадкової величини дисперсію визначають як

D [X(ω)_д] = ∑ (x_i – m_x)² p_i ≡ D_x , (3.18)

i

для неперервної випадкової величини як

∞

D [X(ω)] = ∫ (x – m_x)² ƒ(x) dx ≡ D_x . (3.19)

-∞

Дисперсія випадкової величини править за основну міру варіабельності ("розсіювання") значень випадкової величини, характеризуючи їхню "розкиданість" навколо математичного очікування (як центра розподілу). Детально важливі властивості дисперсії, як і математичного очікування розглянуті у р.4 і р.7. Тут же відзначимо одну з таких властивостей. А саме,

D_x = 0 → P {X(ω) = m_x} = 1 , (3.20)

тобто, якщо дисперсія дорівнює нулю, то єдине значення випадкової величини є її математичним очікуванням і випадкова величина з ймовірністю 1 є константою.

Дисперсія має розмірність квадрата випадкової величини. Для того ж, щоб отримати показник розсіювання значень випадкової величини з розмірністю останньої, використовують її середнє квадратичне відхилення (або стандарт) {σ [X(ω)] або σ_x, "сигма" мала}, яке дорівнює додатному значенню (абсолютній величині) кореня квадратного з дисперсії, тобто

σ [X(ω)] = (μ₂ [X(ω)])^0,5 = (D [X(ω)])^0,5 ≡ σ_x = D_x^0,5 . (3.21)

Застосовують також безрозмірну міру розсіювання значень випадкової величини, а саме її коефіцієнт варіації {C_v [X(ω)] або C_v,x}, що визначається через нормування стандарту за імовірнісним середнім як

C_v [X(ω)] = σ [X(ω)] / M [X(ω)] ≡ C_v,x = σ_x / m_x , (3.22)

або через моменти

C_v [X(ω)] = (μ₂ [X(ω)])^0,5 / m₁[X(ω)] , (3.23)

Увівши поняття математичного очікування та дисперсії і стандарту, доцільно одразу розглянути ще деякі способи перетворення випадкових величин, окрім їхнього центрування [див. формули (3.10)-(3.11)]. Отже, при перетворенні розрізняють також так звані унормовані випадкові величини різного порядку.