Ispit-2
.docПитання на іспит з математичного аналізу
(семестр 2)
Змістовий модуль 4 "Диференціальне числення ФВА"
Означення
Простори: метричний, векторний нормований, евклідів
1. Означення метричного простору. Приклади.
2. Компактна множина.
3. Повний метричний простір.
4. Стискаючий оператор. Нерухома точка оператора.
5. Означення векторного нормованого простору. Приклади.
6. Означення евклідового простору. Приклади.
Функції векторного аргументу (ФВА)
7. Границя функції в точці.
8. Функція, неперервна в точці.
9. Функція, рівномірно неперервна на множині.
10. Частинна похідна в точці.
11. Диференціал. Функція, диференційовна в точці.
12. Градієнт. Похідна функції в напрямі.
13. Похідні і диференціали вищих порядків.
14. Диференційовність
відображення
.
Матриця Остроградського–Якобі. Якобіан.
15. Екстремуми: внутрішній локальний, умовний, глобальний.
Твердження
Простори: метричний, векторний нормований, евклідів
1. Лема про об’єднання і перетин відкритих множин. (З доведенням).
2. Теорема про
векторні послідовності. Повнота простору
.
3. Принцип стискаючих відображень.
4. Лема про метризовність векторного нормованого простору. (З доведенням).
5. Нерівність Коші–Буняковського–Шварца. (З доведенням).
Функції векторного аргументу
6. Границя суми, добутку і частки функцій.
7. Локальні властивості неперервних функції.
8. Глобальні властивості неперервних функцій (теореми: Больцано–Коші про проміжне значення, Вейєрштрасса, Кантора).
9. Зв’язок між неперервністю, диференційовністю та існуванням скінченних частинних похідних.
10. Достатня умова диференційовності. (З доведенням).
11. Теорема про обчислення похідної в напрямі. (З доведенням).
12. Похідна суми, добутку і частки функцій. (З доведенням).
13. Похідна складної функції. (З доведенням).
14. Теорема Шварца про рівність мішаних похідних. (З доведенням).
15. Формула Тейлора. (З доведенням).
16. Теореми про неявну функцію.
17. Необхідна умова внутрішнього локального екстремуму. (З доведенням).
18. Достатня умова внутрішнього локального екстремуму. Критерій Сильвестра. Випадок функції двох змінних.
19. Умовний екстремум скалярної функції векторного аргументу: метод виключення, метод невизначених множників Лагранжа.
20. Найбільше і найменше значення функції на множині.
Змістовий модуль 6 "Кратний інтеграл Рімана"
Означення
1. 
-кратний
інтеграл Рімана на брусі як границя
інтегральних сум.
2. Суми Дарбу, інтеграли Дарбу.
3. Жорданова
множина в
,
її жорданова міра.
4. 
-кратний
інтеграл Рімана по жордановій множині.
Твердження
5. Необхідна умова інтегровності.
6. Критерій Дарбу інтегровності функції на брусі.
7. Критерій Лебега інтегровності функції за Ріманом.
8. Властивості міри Жордана.
9. Властивості
-кратного
інтеграла Рімана, виражені рівностями
і нерівностями. (З доведенням).
10. Теореми Фубіні. Зведення подвійного (з доведенням) та потрійного інтегралів до повторних.
11. Геометричний смисл якобіана заміни. Якобіан заміни для ПСК, ССК, ЦСК.
12. Формула заміни змінних у кратному інтегралі.
Змістовий модуль 7 "Криволінійні і поверхневі інтеграли.
Елементи математичної теорії поля"
Означення
1. Гладка крива
в
.
Криволінійний інтеграл 1-го роду. Довжина
кривої.
2. Гладка поверхня
в
.
Поверхневий інтеграл 1-го роду. Площа
поверхні.
3. Орієнтація гладкої кривої. Криволінійний інтеграл 2-го роду.
4. Орієнтація
гладкої поверхні в
.
Поверхневий інтеграл 2-го роду.
5. Скалярне поля. Типи симетрії скалярного поля.
6. Градієнт скалярного поля.
7. Векторне поле. Векторна лінія. Векторна трубка.
8. Потік і дивергенція векторного поля.
9. Циркуляція і ротор векторного поля.
10. Потенціальне векторне поле і його потенціал.
11. Соленоїдне векторне поле і його векторний потенціал.
12. Диференціальні операції другого порядку в теорії поля.
Твердження
1. Властивості і фізична інтерпретація криволінійних і поверхневих інтегралів.
2. Три інтегральні теореми: Гріна, Остроградського–Гаусса, Стокса. (З доведенням).
3. Умови незалежності криволінійного інтеграла від шляху інтегрування. (З доведенням). Інтегрування повних диференціалів.
4. Теорема про похідну в напрямі (з доведенням).
5. Теорема про збереження інтенсивності векторної трубки. (З доведенням).
6. Три інтегральні теореми: Гріна, Остроградського–Гаусса, Стокса. (З доведенням).
7. Теорема Гельмгольца.
8. Операції теорії поля в КОСК. *
Типи практичних завдань
1. 
,
де
.
Знайти
,
,
.
2. Функція
неявно задана рівнянням
.
Знайти
.
3. 
.
Знайти
,
,
.
4. Написати три доданки формули Тейлора з залишковим членом у формі Лагранжа для функції
в точці
.
5. Знайти
похідну функції
в точці
у напрямі градієнта функції
в цій точці.
6. Знайти
,
,
якщо
.
7. Знайти
якобіан відображення
,
де
8. Перетворити
рівняння
,
якщо
;
.
9. Дослідити
на внутрішній локальний екстремум
функцію
.
10. Знайти
найбільше значення функції
на множині
.
11. Дослідити
на умовний екстремум функцію
,
якщо
.
12. Змінити
порядок інтегрування в інтегралі
.
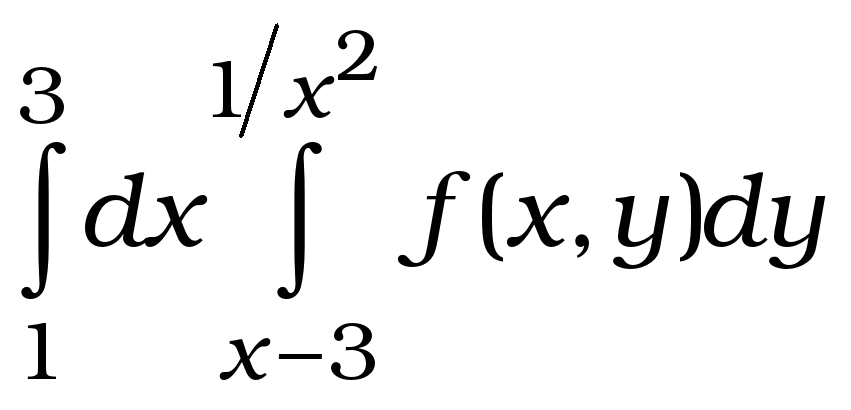13. Перейшовши до полярних координат, обчислити подвійний інтеграл:
а) 
,
якщо
;
б) 
,
якщо
;
в) 
,
якщо
.
14. Знайти
масу, статичні моменти і моменти інерції
фігури
густини
:
а) 
,
;
б) 
.
15. Звівши потрійний інтеграл до повторного двома способами, обчислити об’єм тіла
.
16. Знайти об’єм тіла, обмеженого поверхнею:
а) 
;
б)
;
в) 
.
17. Знайти
масу тіла
густини
:
а) 
,
; б) 
,
;
в) 
,
.
18. Знайти
статичний момент
тіла
.
19. Знайти
масу кривої
лінійної густини
,
якщо
,
,
.
20. Обчислити
координати центру мас однорідної
поверхні
,
якщо
.
21. Знайти
роботу вектора
уздовж кривої
,
якщо
,
від точки
до точки
.
22. Обчислити
потік векторного поля
через ліву сторону поверхні
,
якщо
,
.
23. Перевірити,
що
є повним диференціалом деякої функції
,
якщо
.
Знайти
та обчислити
.
24. Використовуючи
формулу Гріна, обчислити
,
де
–– межа області
.
25.
Застосовуючи формулу Гаусса–Остроградського,
знайти потік вектора
через внутрішню сторону поверхні 
,
якщо
,
.
26. Використовуючи
формулу Стокса, знайти циркуляцію
вектора
уздовж кривої
при напрямі обходу проти годинникової
стрілки з боку додатної півосі
,
якщо
,
.
27. Довести:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
.
28. Обчислити:
а) 
,
–– сталий вектор;
б) 
;
в) 
;
г) 
.
29. Знайти
похідну скалярного поля
в точці
в напрямі від точки
до точки
.
30. Обчислити:
а) 
;
б) 
,
––
сталий вектор.
31. Довести
соленоїдність векторного поля
і знайти його векторний потенціал
.
32. Довести
потенціальність векторного поля
і знайти його потенціал
.
33. Обчислити:
а) 
;
б)
.