3.4. Переходные процессы в электроприводе

При пуске и останове электродвигателя, при его реверсе, изменении задания на скорость или при других управляющих воздействиях в регулируемом электроприводе, при приложении (или снятии) к валу двигателя механической нагрузки изменяются параметры электропривода: ток, момент, скорость двигателя и другие. При этом привод переходит из одного установившегося режима работы с одними параметрами движения в другой с другими параметрами. Однако этот переход не может быть мгновенным, т.к. ток в двигателе из-за электромагнитной инерционности его цепей не может изменяться мгновенно и скорость двигателя из-за механической инерционности движущихся масс электропривода также не может изменяться мгновенно.

Переходным процессом (переходным режимом) электропривода называется процесс, протекающий во времени, перехода от одного установившегося режима работы (или отключенного состояния) к другому установившемуся состоянию.

Причиной возникновения переходных процессов могут быть:

• управляющие воздействия (включение – отключение электропривода, изменение задания на скорость привода и др.);

• возмущающие воздействия, главным из которых является изменение нагрузки на валу двигателя (изменение М_С).

Для расчета и анализа переходных процессов необходимо найти переходную функцию, т.е. зависимость параметров электропривода (скорости, тока, момента и др.) от времени.

Переходные функции описываются дифференциальными уравнениями. Порядок дифференциального уравнения будет равен числу инерционностей, которые учитываются при рассмотрении данного переходного процесса. Такими инерционностями являются:

• механическая инерционность, связанная с накоплением или отдачей кинетической энергии; ее влияние на переходные процессы оценивается электромеханической постоянной времени Т_М (см.2.19);

• электромагнитная инерционность, связанная с накоплением (или отдачей) энергии в электромагнитном поле; электромагнитная инерционность с точки зрения ее влияния на переходный процесс оценивается электромагнитной постоянной времени

, (3.2)

где: L – индуктивность электромагнитного устройства (например, обмотки двигателя); R – активное сопротивление обмотки;

• электростатическая инерционность, связанная с накоплением (отдачей) энергии в электростатическим поле (конденсаторе); эта инерционность оценивается постоянной времени

, (3.3)

где: С – емкость конденсатора, R – сопротивление цепи заряда-разряда конденсатора;

• инерционность, связанной с накоплением потенциальной энергии (например, в упругом элементе механической системы); эта инерционность для учета при анализе переходных процессов отражается величиной, обратной жесткости элемента или другим физическим параметром.

Если предположить, что инерционности отсутствуют или они пренебрежимо малы, то переходные процессы будут протекать мгновенно. Наличие в реальных системах инерционностей различной физической природы обуславливает затягивание переходных процессов, связанное с тем, что в процессе перехода системы из одного состояния в другое происходит накопление (запасание) или отдача энергии, которые не могут происходить мгновенно.

Если потоки энергии однонаправлены, то переходный процесс при приложении постоянного по величине воздействия носит монотонный характер. Таков, например, процесс нарастания тока в обмотке возбуждения двигателя постоянного тока при подаче напряжения на эту обмотку (рис.3.8а).

Процесс изменения тока во времени описывается дифференциальным уравнением приводя который к нормализованному виду с учетом (3.2), получим:

(3.4)

или в операторной форме:

. (3.5)

Решение этого уравнения будет

(3.6)

при

(3.7)

Переходная характеристика представляет собой экспоненту (рис.3.8б). За время, равноеТ_Э, ток в обмотке возбуждения возрастает до значения 0,63I_уст; за время 3Т_Э - до значения 0,95I_уст; за время 5Т_Э - до значения 0,98I_уст. Практически можно считать, что время переходного процесса при экспоненциальном характере переходного процесса составляет 3-5 постоянных времени. Если возникает задача ускорить нарастание тока в обмотке возбуждения, то это можно сделать единственным способом – увеличить напряжение, подводимое к индуктивности (обмотке возбуждения) на время протекания переходного процесса. Если, например, мы увеличим напряжение в а раз , то ток в обмотке возбуждения будет нарастать быстрее, как это следует из характеристики 2 на рис.3.8б. По достижении током значенияI_уст напряжение на обмотке возбуждения следует уменьшить до значения .

Таким образом, для уменьшения времени переходного процесса нужно применить форсировку напряжения, которая затем снимается. Отношение называется коэффициентом форсировки.

Переходные процессы в электроприводе, когда изменяются ток, момент и скорость двигателя, представляют собой сложное явление – одновременное протекание электромагнитных и механических переходных процессов. Характер переходного процесса зависит от числа инерционностей, участвующих в данном процессе, и соотношения между характеризующими их постоянными времени.

Если постоянные времени по величине отличаются на два и более порядка, то можно малыми постоянными времени пренебрегать. Это упрощает анализ переходных процессов.

Переходные процессы в зависимости от характера объекта могут описываться линейными или нелинейными дифференциальными уравнениями. Если нелинейности несущественны, можно прибегнуть к линеаризации уравнений.

В случае линейных систем анализ переходных процессов (расчет переходных характеристик) может производиться аналитическими методами. В случае нелинейных систем целесообразно пользоваться численными методами решения уравнений на ЭВМ или методами компьютерного моделирования.

Проведем анализ переходных процессов, характеризующихся двумя инерционностями: механической и электромагнитной. Рассмотрим изменение скорости двигателя, имеющего линейную механическую характеристику, при приложении управляющего и возмущающего воздействий.

Момент двигателя при линейной механической характеристике равен (см.рис.3.3)

. (3.8)

Момент в общем случае пропорционален току в обмотках двигателя . При приложении (изменении) управляющего воздействия: напряжения (для двигателя постоянного тока), напряжения и частоты (для асинхронного двигателя), - будет изменяться ток в обмотках двигателя. Однако, поскольку обмотки обладают индуктивностью, ток а, следовательно и момент, будут изменяться не мгновенно, а в функции времени. Электромагнитная часть двигателя описывается апериодическим (инерционным) звеном с постоянной времениТ_Э. По аналогии с (3.5), умножая ток I на с_м, получим . С учетом (3.8) процесс изменения момента в этом случае описывается дифференциальным уравнением

(3.9)

Решая это уравнение совместно с уравнением движения (2.8) и учитывая, что и, после преобразований получим

(3.10)

Здесь - установившееся значение скорости, с которой будет работать двигатель по окончании переходного процесса; еслиМ_С=0, то .

Характеристическое уравнение для (3.10) будет:

. (3.11)

Корни этого уравнения .

Если, то корни будут вещественными и отрицательными. В этом случае решение уравнения (3.10) имеет вид:

. (3.12)

П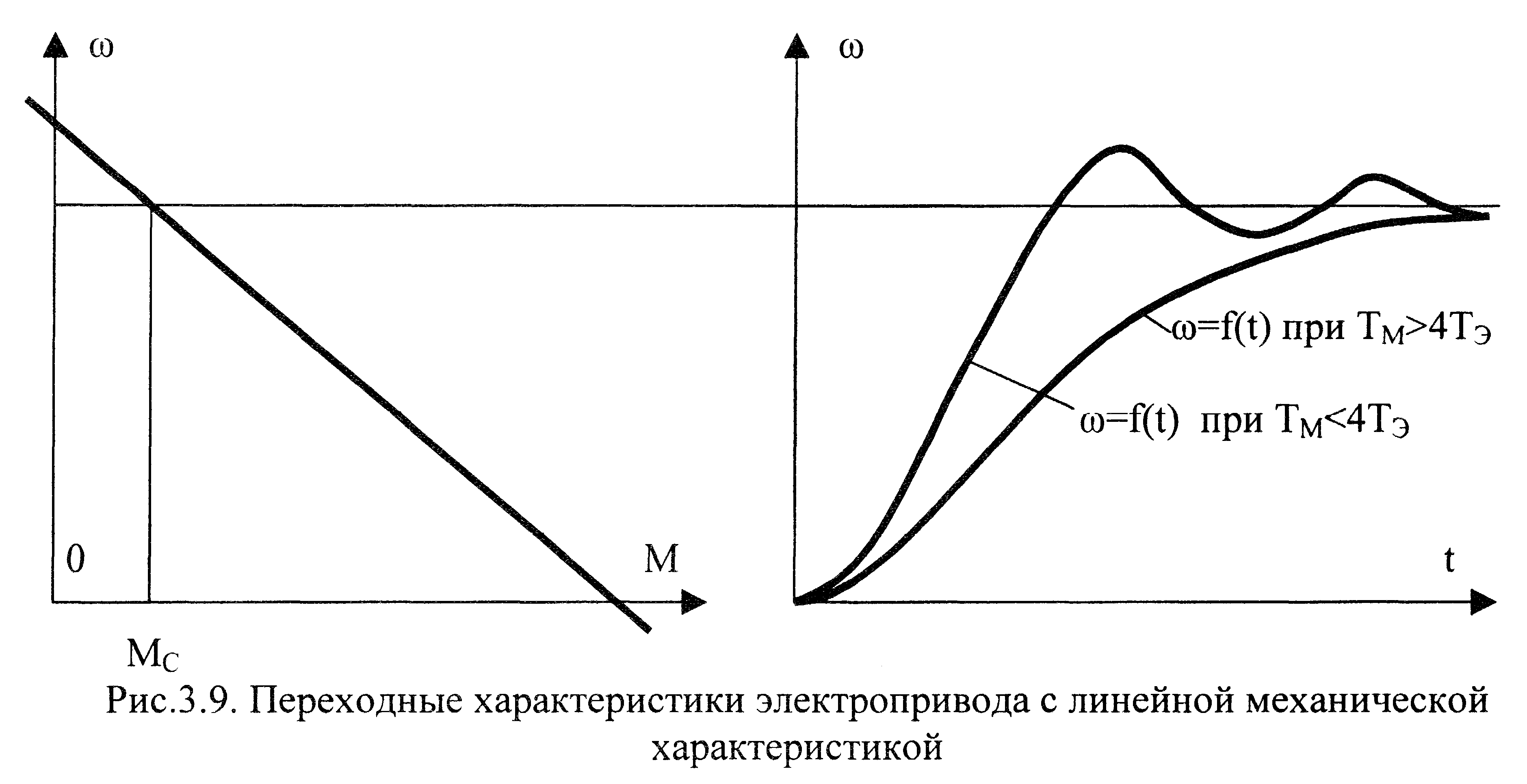ереходный процесс в этом случае будет носить монотонный характер с изменением скорости по закону, соответствующему инерционному звену второго порядка (см.рис.3.9).

Если , то корни будут комплексными сопряженными с отрицательной вещественной частью, где

(3.13)

Решение дифференциального уравнения (3.10) при этом будет:

. (3.14)

Постоянные интегрирования С₁ и С₂ находятся из начальных или конечных условий переходного процесса, например при t=0 .

Переходный процесс в этом случае характеризуется периодическими колебаниями с частотой Ω и затухающей амплитудой. Время переходного процесса ориентировочно может быть оценено, как . Колебательность процесса связана с тем, что происходит периодическое преобразование кинетической энергии в электромагнитную и обратно.

Представив уравнения (3.9) и (2.8) в операторной форме

с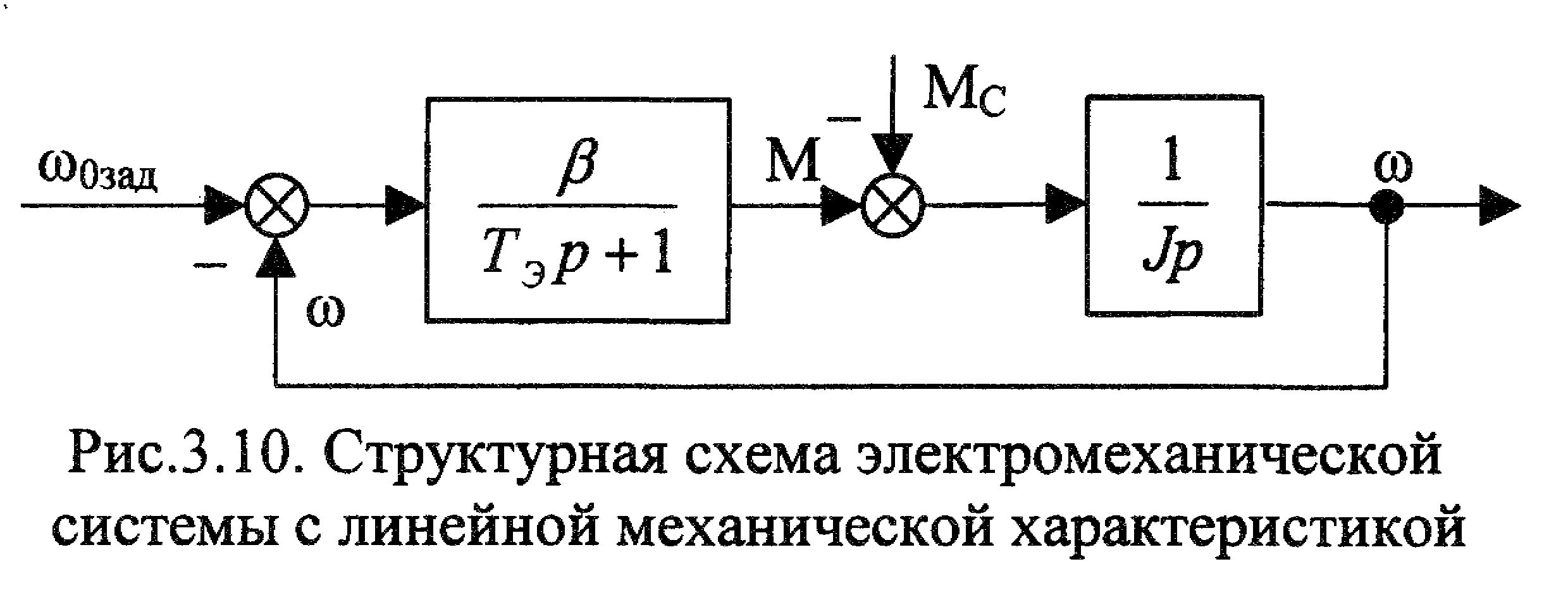оставим структур-ную схему (рис.3.10), отражающую дина-мические свойства электропривода с ли-нейной механической характеристикой.

Скорость холостого хода ω₀ пропорциональна сигналу задания

.

В соответствии со структурной схемой найдем передаточную функцию электропривода (по управляющему воздействию )

. (3.15)

Знаменатель этой передаточной функции идентичен левой части характеристического уравнения (3.11), что говорит о том, что переходная функция при единичном управляющем воздействии будет описываться уравнением (3.12) прии уравнением (3.14) при.

Найдем передаточную функцию электропривода при возмущающем воздействии.

; (3.16)

отсюда . (3.17)

Это выражение показывает, что при приложении к двигателю нагрузки – статического момента , скорость двигателя уменьшится на величину.

Процесс перехода от начальной скоростиω₀ при М_С=0 к новому установившемуся значению ω_уст при может носить монотонный характер, еслиТ_м>4Т_я, или затухающий колебательный характер, если Т_м<4Т_я. Характеристики переходного процесса показаны на рис.3.11.

В общем случае можно предложить следующий порядок анализа переходных процессов в системах электропривода, если эти процессы описы-ваются линейными (или линеаризованны-ми) дифференциаль-ными уравнениями.

1. Определяется, какие инерционности следует учитывать при анализе данного переходного процесса.

2. Находят постоянные времени, характеризующие каждую инерционность. Если постоянные времени отличаются на 2 и более порядка, то меньшими в инженерных расчетах, как правило, можно пренебречь.

3. Число инерционностей определяет порядок дифференциального уравнения, описывающего переходный процесс.

4. Находят характеристическое уравнение, соответствующее левой части однородного линейного дифференциального уравнения, описывающего исследуемый переходный процесс. Характеристическое уравнение будет иметь вид (например, для дифференциального уравнения 3-го порядка) . ЗдесьТ₁, Т₂, Т₃ – постоянные времени.

5. Переходный процесс в случае линейных зависимостей переменных и скачкообразного (единичного) характера управляющего или возмущающего воздействий будет описываться уравнением , (гдеХ – исследуемый параметр электропривода – ток, момент, скорость) вида (например, для уравнения 3-го порядка) если все корни характеристического уравнения действительные и, если один корень характеристического уравнения действительный, а остальные два – комплексно сопряженные

.