25.2. Электропривод турбомеханизмов

25.2.1. Характеристики турбомеханизмов

Наиболее характерными видами турбомеханизмов являются механизмы центробежного типа, предназначенные для транспортировки жидкости – насосы, газа – вентиляторы, сжатого воздуха - турбокомпрессоры. К механизмам этого же класса относятся осевые вентиляторы и насосы.

Работу центробежных механизмов рассмотрим на примере центробежного насоса, который состоит из рабочего колеса с лопатками и корпуса спиральной формы. При вращении рабочего колеса жидкость увлекается лопатками и под действием центробежной силы и силы кориолиса движется от центра колеса к его периферии вдоль лопаток, затем подается через спиральную камеру в нагнетательную трубу. При этом в центре корпуса создается разряжение, под действием которого вода через всасывающую трубу подается в насос. Частицы жидкости участвуют в двух движениях: вращательном вместе с колесом, приобретая окружную скорость, и линейном вдоль лопаток, приобретая относительную линейную скорость.

Мощность, развиваемая насосом или вентилятором, выводится из выражения энергии, сообщаемой движущейся жидкости (газу) в единицу времени

(25.3)

где: - масса жидкости, проходящая через нагнетательную трубу, кг/с;V - скорость жидкости, м/с; S - поперечное сечение нагнетательного трубопровода, м²; - плотность жидкости, кг/м³.

Подставляя значение массы в уравнение (25.3) получим, что мощность

кВт. (25.4)

Если учесть, что SV=Q – подача насоса м³/с, - напор (удельное давление), Н/м² (Па), то мощность и момент на валу двигателя определятся из выражения:

(25.5)

где: ω - скорость двигателя, с^-1; η - кпд насоса, включающий гидравлический кпд η_г=(0,8...0,96) и объемный η_о=(0,96...0,98).

Напор часто выражают в метрах водяного столба. В этом случае кВт.

Принимая, что скорость движения жидкости V=ωR, где: R – радиус колеса

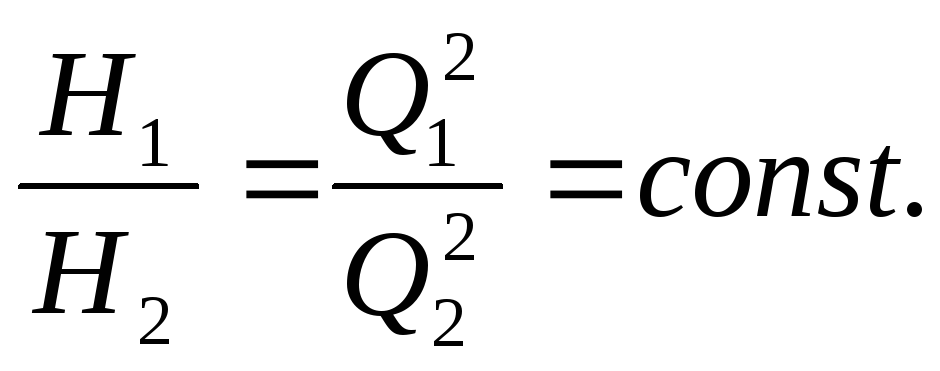, ,(25.6)

Зависимости момента и мощности на основании (25.5) и (25.6) выражаются соотношениями:

(25.7)

Э

Рис.25.5. Q-H-характеристики механизмов центробежного типа

ксплуатационные свойства механизмов центробежного типа определяютсяQ-H-характеристикой и зависимостью механической мощности и кпд от подачи приω=cоnst. Расчет указанных хара-ктеристик представляет трудности, поэтому на практике пользуются ти-повыми зависимостямиН=f(Q)иη=f(Q),Р=f(Q), которые приводятся в каталогах для насосов при неизменной номи-нальной скоростиω_н(рис.25.5)Q-H-характе-ристики для скорости, отличной от номинальной, получают с помощью уравнений пропорциональности (25.6), (25.7).

Для этого задается ряд значений Q_е, которым соответствует значение Н_е исходной естественной характеристики с ω_н=const. В соответствии с (25.6) рассчитывают параболы , проходящие через выбранные точкина исходной характеристике. Каждой точке параболы согласно (25.6) соответствует определенная скорость механизма. Соединяя точки парабол с одинаковым значениемω, определяют Q-H-характеристику для ω=const. Так как уравнения пропорциональности получены в предположении постоянства η_г и η_о, то указанные параболы (кривые 3) оказываются линиями постоянного кпд механизма.

Установившийся режим работы насоса при постоянной скорости определяется графическим или аналитическим способами. При графическом - установившийся режим определяется точкой пересечения соответствующей Q-H-характеристики турбомеханизма и характеристики магистрали, подключенной к насосу.

(25.8)

где: Н_ст=Н_вс+Н_наг - сумма высот всасывания и нагнетания. Если насос находится ниже уровня всасывания, Н_ст=Н_наг-Н_вс. При отсутствии статического напора характеристика трубопровода имеет вид кривых 3 (рис.25.5).

Если скорость расчетной точки отличается от номинальной, то соответствующее этой скорости значение кпд определяется следующим образом. Через расчетную точку (например Р на рис.25.5) проводится парабола до пересечения с номинальной Q-H-характеристикой. Точка пересечения дает значение Q_e2, которое определяет по кривой η=f(Q)значение кпд.

При аналитических расчетах Q-H-характеристику описывают эмпирической формулой.

, (25.9)

где значения Н₀ (или А) и С определяют по двум точкам известной Q-H-характеристики. Одну точку целесообразно брать в начале кривой (при Q=0), а вторую в рабочей зоне. Тогда в первой точке Н=Н₀, а во второй . ЗначениеА определяется из формулы Кпд при скоростях, не равныхω_н, определяют из следующих соотношений:

(25.10)

где: Q_и и η_и - производительность и кпд при номинальной скорости; Q_A, Q_B, η_A, η_B - производительность и кпд в начале и конце заданного отрезка.

Более точные формулы для определения Q, H, P и η, особенно для вентиляторов, предложены в [4-22]

(25.11)

Здесь для определения коэффициентов А, В, С, А₁, В₁, D₁ необходимо составлять три уравнения по известным Q-H и Р_мех-Q-характеристикам.

Структурная гидромеханическая схема насосной установки с магистралью протяженностью до 100м представлена на рис. 25.6. Здесь жидкость принята несжимаемой. При более длинных магистралях необходимо учитывать упругость жидкости и трубопроводов.

Рис.25.6. Структурная гидромеханическая схема насосной установки

Структурная схема составлена на основе системы уравнений без учета динамической составляющей :

(25.12)

где: - инерционная составляющая давления; R_м - сопротивление магистрали; l - длина трубопровода.