
- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
Производственные функции. Агрегирование и дезагрегирование
Производственные функции отражают зависимость результатов производства от объема затрачиваемых ресурсов и фактически представляют собой упрощенную экономико-математическую модель производства.
На примере двухфакторной модели (число агрегированных видов ресурсов равно двум) приведем наиболее часто встречающиеся на практике виды производственных функций (ПФ).
Итак, пусть x1 и x2 – объемы затраченных ресурсов, Р – результат производства (объем произведенной продукции).
Линейная ПФ:
Р=а1 х1+а2х2 ,
где а1 и а2 – коэффициенты эффективности используемых ресурсов.
Линейные ПФ используются при анализе крупномасштабных систем (отрасль, народное хозяйство в целом). При этом используются агрегированные коэффициенты эффективности.
Кроме того, линейные ПФ могут использоваться и в нелинейном варианте при сравнительно небольших изменениях объемов затрачиваемых ресурсов, что позволяет использовать линейную аппроксимацию изначально нелинейных ПФ.
ПФ с фиксированными пропорциями факторов
Р=min
 ,
, .
.
Такие ПФ используются для моделирования производственных систем, в которых используются технологии с жестко фиксированными нормами затрат ресурсов. Например, при сборке одного автомобиля необходимо наличие одного двигателя (х1) и четырех колес (х2), при этом а1=1, а2=4 – отражают пропорции объемов затрачиваемых ресурсов (комплектующих – двигателей и колес). В таких производствах ресурсы не могут заменять друг друга.
ПФ Аллена:
Р=а0х1х2-а1х12-а2х22
Имеет вид параболы по каждому виду ресурсов. Такие ПФ используются для моделирования производственных процессов, в которых неограниченный рост любого из факторов приводит к уменьшению объема выпуска.
Примером такого производства может служить производство сельскохозяйственной продукции, объем которого именно так зависит от объема полива и используемых удобрений.
ПФ Кобба-Дугласа:
Р=а0 .
.
В этой модели коэффициенты а1>0 и а2>0 являются коэффициентами эластичности по соответствующему виду ресурсов.
При этом, как правило, считается, что
а1+а2=1,
то есть эта ПФ является линейно однородной, следовательно, характеризуется постоянной отдачей при изменении масштабов производства.
Число видов ПФ, используемых различными исследователями в различных ситуациях великое множество. Мы привели наиболее интересные, которые будут изучаться далее.
Вернемся к понятию ПФ, как экономико-математической модели. Как всегда, при построении такой модели возникает вопрос точности и подробности описания. Ответ на этот вопрос имеет качественный характер – точность описания должна быть согласована с возможностью анализа модели и ясностью получаемых рекомендаций.
Отметим также некоторые полученные свойства моделей, связанных с агрегированием.
Агрегирование
Пусть производственная система (объединение) состоит из n различных по технологии производств, производственные функции которых имеют вид (см. лекцию 2):
Рi=ai ,
i=
,
i= .
.
Построим производственную функцию объединения
Р=Ф(Х),
 Эта
функция должна описывать оптимальную
(!) зависимость максимально возможного
суммарного объема произведенной
продукции от суммарного объема
затрачиваемых ресурсов.
Эта
функция должна описывать оптимальную
(!) зависимость максимально возможного
суммарного объема произведенной
продукции от суммарного объема
затрачиваемых ресурсов.
Таким образом, построение этой ПФ тесно связано с решением следующей задачи оптимизации распределения ресурсов по технологиям:

Pi=ai ,
xi
,
xi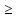 0,
i=
0,
i= ,
,

Как было показано выше, решение этой задачи имеет вид:

Соответственно
Pi=ai =
=
Отсюда следует, что

Обозначим

Окончательно получим (агрегированную) ПФ объединения
P=A ,
,
Где А- коэффициент экономической эффективности затрат ресурсов для всего объединения.
Для иллюстрации приведем числовой пример.
Пусть n=2, a1=3,a2=4.
Тогда
А=
Значит
Р=5 .
.
Заметим, что в этом примере, как и в общем случае анализируемой ПФ имеем:

То есть при оптимальном распределении ресурсов «осредненная» по объединению технология эффективнее самой эффективной технологии.
Таким образом, ПФ выражает зависимость произведенной продукции от объема затрачиваемых ресурсов при оптимальном их использовании как в технологическом, так и в экономическом смысле.
