
- •Московский Государственный открытый университет
- •Понятие хозяйственного механизма
- •Базовая модель
- •Общая схема формализации процессов моделирования хозяйственного механизма
- •Лекция 2 Базовая модель в контексте формализованной схемы моделирования хозяйственного механизма
- •Производственные функции. Агрегирование и дезагрегирование
- •Лекция 3 Синергетический эффект
- •Эффективность создания совместного производства (системы)
- •Механизм инноваций
- •Лекция 4 Многокритериальные задачи
- •Поиск эффективных точек
- •Лекция 5
- •Формализация основных понятий Теории Игр.
- •Принцип Оптимальности
- •Принятие решений
- •Принцип Оптимальности
- •2 Фирма
- •1 Фирма
- •Роль информированности. Формализация информированности в виде стратегии
- •Лекция 6 Ситуация равновесия по Нэшу в информационном расширении игры
- •Формальное определение
- •Информационное расширение игры
- •Примеры проектирования множества стратегий на множество управлений (выборов, исходов)
- •Ситуация равновесия по Нэшу в информационном расширении игры
- •2 Фирма
- •1 Фирма
- •Лекция 7 Иерархические системы управления
- •Обобщенный принцип максимального гарантированного результата (оп мгр)
- •Иерархическая игра (игра Гермейера)
- •Экономическая интерпретация иерархических игр г1, г2и г3
- •Лекция 8 Теоретико-игровой анализ двухуровневой иерархической системы управления (ису)
- •2.Аналог игры
- •Лекция 9 Динамические модели принятия решений
- •Слабоустойчивые совместные решения по ю. Б. Гермейеру
- •Динамическая модель принятия решений с непрерывным временем
- •Оптимизация процесса контроля (наблюдения)
- •Литература
- •Лекция 10 Управление ису при неточном знании параметров подсистем
2 Фирма
реклама не реклама
реклама
4,4 9, 0 
1 Фирма
не реклама 0,9 5,5
Элементы матриц выигрышей имеют следующий смысл:
(4,4) – обе фирмы потратятся на рекламу и тогда поровну распределится объем рынка, их продукцию будут покупать, так как она разрекламирована, фирмы получат выигрыш M1= M2 = 4.
(9,0) – если 1-я фирма потратит деньги на рекламу, а вторая не будет этого делать, тогда в выигрыше будет 1-я фирма, так как ее товар все будут покупать: ее выигрыш M1= 9, а вторая фирма ничего не получитM2 = 0.
(0,9) – наоборот, первая фирма не рекламирует свой товар, а вторая – рекламирует, тогда вторая фирма будет в выигрыше, займет весь оставшийся объем рынка M2 = 9, а первая ничего не получитM1= 0.
(5,5) – обе фирмы ничего не рекламируют и в результате делят объем рынка пополам M1= M2 = 5.
В этой игре ситуация равновесна – точка (4,4), когда товар обеих фирм хорошо разрекламирован (ситуация равновесия по Нэшу).
Однако, есть точка (5,5) – это Паретовская точка (т.е. обе фирмы могут получить больше на одинаковое количество). Эта ситуация возможна тогда, когда никто не будет друг друга обманывать, а для этого необходимы дополнительные переговоры.
Итак, ситуация равновесия в этом примере существует и единственна, но она не устраивает обоих игроков.
Роль информированности. Формализация информированности в виде стратегии
Напомним основные понятия теории игр.
Пусть задана игра:
 ,
далее будем использовать запись
,
далее будем использовать запись .
.
Здесь
 - множества управлений,
- множества управлений,
 ,
где
,
где - управление .
- управление .

 - функция выигрыша игрокаi, i=1,2
- функция выигрыша игрокаi, i=1,2
Пусть
 -
информационное множество игрока i
-
информационное множество игрока i
 -
информация, доступная игроку i
-
информация, доступная игроку i
Стратегия – функция, зависящая от информации:

 - множество стратегий игрока i
- множество стратегий игрока i
Например: - игрок 1 перед выбором
- игрок 1 перед выбором будет знать выбор
будет знать выбор ,
т.е. в этом случае:
,
т.е. в этом случае: ;
;
 - множество функций
- множество функций .
.
Ход игрока i -- выбор стратегии
 и сообщение информации о своем выборе
партнерам (сообщение может быть «пустым»):
и сообщение информации о своем выборе
партнерам (сообщение может быть «пустым»):
Роль информированности
Покажем на примерах как наличие информации влияет на выбор решения и соответственно на ожидаемый результат.
Пример 1: Информация о выборе партнера
Рассмотрим антагонистическую игру:
 .
.
Пусть первый игрок не имеет информации о выборе второго игрока х2 до своего выбора управления х1.
Тогда его оптимальный ( максимально гарантированный результат – МГР) равен:

Пусть теперь первый игрок будет иметь
информацию о выборе
 вторым
игроком.
вторым
игроком.
Тогда игрок 1 может использовать абсолютно
оптимальную стратегию

 , такую что
, такую что при любых
при любых .
.
В этом случае оптимальный (МГР) результат игрока1 равен:

Всегда верно неравенство:
 ,
,


 .
.
Приведем пример когда
 :
:
Пусть функция выигрыша первого игрока
имеет вид:
 ,
, ,
i=1,2
,
i=1,2
В этом случае, не имея информации о
выборе
 игрок 1 (ожидая выбора
игрок 1 (ожидая выбора )
может рассчитывать только на глобальный
минимум:
)
может рассчитывать только на глобальный
минимум:
Пусть теперь игрок 1 будет знать
 до выбора
до выбора .
Построим абсолютно оптимальную стратегию
игрока 1:
.
Построим абсолютно оптимальную стратегию
игрока 1:

Рис.1.
Итак,
 =
=
Функция
 имеет вид (см. рис. 2):
имеет вид (см. рис. 2):


Рис.2.
Тогда оптимальный ответ второго игрока:

Что дает первому игроку:
 =
=
Таким образом, получение своевременной информации о выборе партнера (противника) может дать ощутимый выигрыш.
Пример 2: Роль информации о правиле поведения (о принципе оптимальности) партнера.
Рассмотрим игру:
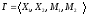 .
Предположим, что первый игрок знает,
что игрок 2 осторожен, т.е. придерживается
принципа максимального гарантированного
результата, а, следовательно, выбирает
.
Предположим, что первый игрок знает,
что игрок 2 осторожен, т.е. придерживается
принципа максимального гарантированного
результата, а, следовательно, выбирает из множества
из множества :
:
 ,
если
,
если

Заметим, что осторожность игрока 2 может обуславливаться отсутствием у него информации о правиле поведения (функции выигрыша) игрока 1.
Итак, если игрок 1 не знает правило поведения игрока 2, то его оптимальный (МГР) результат равен:

Если же игрок 1 знает отмеченное выше правило поведения игрока 2, то его оптимальный выигрыш оценивается величиной:

Так как
 ,
то всегда
,
то всегда
Замечание: Знать правило поведения
(принцип оптимальности) это значит знать
функцию ,
множество
,
множество и принцип выбора (в данном случае МГР).
и принцип выбора (в данном случае МГР).
Покажем, что возможно строгое неравенство
 .
.
Пусть, например, функции выигрышей имеют вид:


 ,
i=1,2
,
i=1,2
Тогда имеем:
 ,
,
 ,
,

 Итак,
дополнительная информация – информация
о правиле поведения партнера дает
дополнительный выигрыш.
Итак,
дополнительная информация – информация
о правиле поведения партнера дает
дополнительный выигрыш.
Замечание: При моделировании
конфликтных ситуаций всегда нужно
фиксировать информированность, например,
игрока 1 о параметрах модели, описывающих
игрока 2: и т.д.
и т.д.
