Министерство образования РФ.

Московский Государственный Университет Машиностроения (МАМИ)

Курсовая работа

по дисциплине «Дискретная математика»

на тему: «Потоки в сетях».

Выполнил студент II курса, Механико-технологического факультета (бакалавр, 010400.62) Вагайцев Д.С. 1912146 Руководитель: Нефедова И. В.

Москва 2013

Содержание:

1. Основополагающие понятия теории сетей:

• ориентированный граф

• сеть

• поток в сети

• разрез в сети

2. Теорема Форда-Фалкерсона и ее доказательство

3. Дополнительные леммы и их доказательство

4. Алгоритм решения задач

5. Решение задач

6. Источники информации

Ориентированный граф - это граф, на ребрах которого обозначены разрешенные направления движения, проще говоря, расставлены стрелочки. Такая, на первый взгляд "мелочь" настолько сильно меняет идеологию решения задач, что ориентированные графы мы рассматриваем отдельно от неориентированных.

В обычных графах мы рассматриваем такие фундаментальные понятия, как степень вершины, путь и цикл, компонента связности. Для ориентированных графов их надо существенно модифицировать: - ребро входит в вершину, если по нему можно двигаться в направлении к этой вершине, и выходит из вершины, если по нему можно двигаться в направлении от этой вершины; - входящая степень вершины - это число входящих в нее ребер; - исходящая (или выходящая) степень вершины - это число выходящих из нее ребер; - путь из вершины A в вершину B - это последовательность ребер и промежуточных вершин, по которым можно дойти из A в B; длина пути определяется, как обычно (число ребер); простой путь - как обычно, путь, в котором вершины (и тем более, ребра) не повторяются; - ориентированный цикл - это замкнутый простой путь в ориентированном графе; - сильно связный ориентированный граф - это ориентированный граф, где из любой вершины в любую есть путь (для каждой пары вершин A и B есть как путь из A в B, так и путь из B в A); - компонента сильной связности - это часть графа, которая сама по себе сильно связна, но ее нельзя расширить так, чтобы она осталась сильно связной; между разными компонентами сильной связности могут быть ребра, но все ребра между двумя разными компонентами направлены в одну и ту же сторону.

Сетью называется пара (G,a), где G – ориентированный граф, а a - функция из множества вершин графа в множество неотрицательных действительных чисел.

Если е – дуга графа G, то число a(е) в зависимости от контекста называется либо длиной, либо весом, либо пропускной способностью дуги. При изображении сети a(е) проставляется рядом с дугой е. В этом параграфе число a(е) будет называться длиной дуги е.

Для сетей можно обобщить понятие полустепени исхода и полустепени захода вершины. Пусть N=(G, a) – сеть, v – вершина этой сети (т.е. вершина графа G). Полустепенью исхода r^–(v) вершины v назовем сумму a(е) по всем дугам, исходящим из v, полустепенью захода r⁺(v) вершины v – сумму a(е) по всем дугам, заходящим в v. Например, для сети на рис. 6.12 выполняется равенство r^–(v₀)=5, r⁺(v₀)=0, r^–(v₂)=8, r⁺(v₂)=4. Для сетей, так же как и для орграфов справедливо утверждение о том, что сумма полустепеней исхода и сумма полустепеней захода всех вершин совпадают.

Как и в случае орграфов, вершину сети v, для которой r^–(v)>0 и r⁺(v)=0 будем называть источником, а вершину w, для которой r⁺(w)>0 и r^–(w)=0 – стоком.

Введем длину пути как сумму длин дуг, составляющих путь.

Определение. Расстоянием d(u,v) от вершины u до вершины v называется длина кратчайшего (u,v)–пути. Если (u,v)–пути не существует, то полагаем d(u,v)=¥. Расстояние от u до u равно нулю.

Так для сети, изображенной на рис. 6.12, имеем равенства d(v₀,v₅)=3, d(v₁,v₀)=¥, d(v₁,v₂)=4, d(v₂,v₁)=2.

Для сети N возникает задача нахождения расстояния d(u,v) для данных вершин u и v и соответствующего кратчайшего пути. Известно несколько способов решения этой задачи. Мы рассмотрим один из них, основой которого является алгоритм Дейкстры, названный в честь известного скандинавского специалиста по компьютерным наукам Дейкстры.

Алгоритм Дейкстры вычисляет расстояние от фиксированной вершины v₀ до всех остальных вершин сети. Прежде, чем привести описание алгоритма, введем необходимые обозначения. Пусть N=(G,a) – сеть, v₀ – фиксированная вершина этой сети, v₁,…,v_k – остальные вершины. Для i=1,…,k расстояние d(v₀,v_i) обозначим через d(v_i). На множестве вершин введем двухместную функцию a(v,v’) следующим образом:

Описание алгоритма, кроме того, еще использует подмножество S множества вершин V.

Алгоритм Дейкстры.

Шаг 1. Полагаем S=V\{v₀}, d(v_i)=a(v₀,v_i) для всех i=1,…,k.

Шаг 2. Если ½S½=1, то выполнить шаг 4. Выбрать в S элемент v’, для которого величина d(v’) является наименьшей (среди всех элементов из S).

Шаг 3. Положить S=S\{v’}, d(v)=min{d(v), d(v’)+a(v’,v)} для всех vÎS и перейти к шагу 2.

Шаг 4. Выдать d(v₁),…,d(v_k). Конец работы алгоритма.

Алгоритм осуществляет «итеративный» процесс нахождения расстояния d(v_i) для i=1,…,k. Проследим, как это делается для сети N, изображенной на рис. 6.12. Работа алгоритма будет иллюстрироваться заполнением таблицы 6.1.

При выполнении первого шага алгоритма величины d(v_i) примут значения, которые указаны в нулевой строке таблицы. Из них точным является только d(v₂), значения остальных величин завышены. На шаге 2 в качестве v’ выбирается вершина v₂ (в таблице соответствующее значение набрано жирным шрифтом) и удаляется из S на шаге 3. На том же шаге уточняются предыдущие значения d(v) для vÎS (см. первую строку таблицы 6.1). На этом первый проход алгоритма заканчивается. На втором проходе в качестве v’ берется v₅, удаляется из S и значения d(v) для vÎS снова уточняются. Результат уточнения отражен во второй строке таблицы. Когда множество S будет содержать только вершину

Рис. 6.12

Таблица 6.1

Номер строки	d(v1)	d(v2)	d(v3)	d(v4)	d(v5)
0	4	1	¥	¥	¥
1	3		¥	5	3
2	3		¥	4
3			4	4
4			4

V₃ алгоритм заканчивает работу. Результат: d(v₁)=3, d(v₂)=1, d(v₃)=4, d(v₄)=4, d(v₅)=3.

Поскольку на каждом проходе алгоритма число элементов множества S уменьшается на единицу, то алгоритм Дейкстры всегда заканчивает работу. Следующее утверждение показывает, что он выдает «то что нужно».

Пусть N=(G,a) – сеть, имеющая один источник a и один сток b. Предположим, что сеть N представляет собой схему линий связи, где вершинам соответствуют узлы связи, дугам – линии связи с указанным направлением передачи информации. Если е – дуга сети N, то величина a(е) означает ограничение количества информации, передаваемой по дуге е за некоторый промежуток времени. Возникает следующий вопрос. Какое наибольшее количество информации можно передать из а в b и как это сделать? Ответу на поставленный вопрос и посвящен этот параграф.

Следуя приведенной выше интерпретации сети, условимся величину a(е) называть пропускной способностью дуги е.

Центральным понятием параграфа является понятие потока в сети.

Рис. 6.15

Рис. 6.16

Определение. Пусть N=(G,a) – сеть, а – источник и b – сток этой сети. Потоком через сеть N называется функция

j:Е®R⁺È{0},

удовлетворяющая двум условиям:

1) J(е)£a(е) для любой дуги еÎе,

2) В сети (g,j) у любой вершины, кроме источника и стока, полустепень исхода равна полустепени захода. Число j(е) называется значением потока через дугу е.

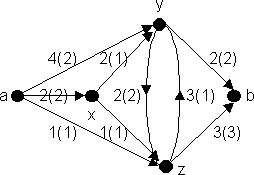
На рис. 6.16 приведен пример потока через сеть, изображенную на рис. 6.15. Значения функции j указаны в скобках.

Предложение. Пусть j - поток через сеть N=(G, a). Тогда сумма потоков через дуги, инцидентные источнику, равна сумме потоков через дуги, инцидентные стоку.

Доказательство. Пусть V={v₁,v₂,…,v_n}, причем v₁ – источник, v₂ - сток. Рассмотрим сеть N’=(G,j). В сети N’ сумма полустепеней исхода всех вершин равна сумме полустепеней захода всех вершин

r^–(v₁) + r^–(v₂) + r^–(v₃) +… + r^–(v_n) = r⁺(v₁) + r⁺(v₂) + r⁺(v₃) + … + r⁺(v_n),

поскольку для любой дуги е число j(е) участвует ровно один раз, как в левой, так и в правой сумме. Так как j - поток, то r^–(v_i) = r⁺(v_i) для i=3,…,n. Это означает, что r^–(v₁) +r^–(v₂) = r⁺(v₁) + r⁺(v₂). Из последнего равенства получаем равенство r^–(v₁) = r⁺(v₂), потому что

r^–(v₂) = 0 и r⁺(v₁) = 0.

Предложение доказано.

Определение. Сумма, о которой говорится в доказанном выше предложении называется величиной потока. Поток называется максимальным, если он имеет наибольшую величину (среди всех потоков через данную сеть).

Величину потока j будем обозначать через ½j½. Поток, приведенный на рис. 6.16, имеет величину 5. Этот поток является максимальным, поскольку его значение на дугах, инцидентных стоку, равно сумме пропускных способностей этих дуг. Сеть может иметь несколько максимальных потоков, как показывает пример, приведенный на рис. 6.17

Рис. 6.17

Рис. 6.18

При изучении максимальных потоков в сети используется понятие разреза.

Определение. Разрезом сети N, имеющей один источник и один сток, называется множество дуг S такое, что любой путь из источника в сток проходит через дугу из S.

Определение. Пропускной способностью разреза называется сумма пропускных способностей входящих в него дуг. Разрез называется минимальным, если он имеет наименьшую пропускную способность (среди всех разрезов данной сети). Пропускную способность разреза S будем обозначать через a(S).

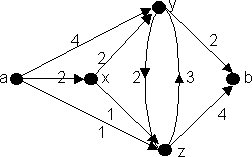
Так, например, для сети на рис. 6.18 примерами разрезов будут множества S₁={(a,y), (a,x), (a,z)}, S₂={(a,z), (x,z), (y,z), (y,b)}, S₃={(y,b), z,b)}. Эти разрезы имеют пропускные способности соответственно 7,6 и 6. Разрезы S₂ и S₃ являются минимальными. Мы видим, что минимальных разрезов может быть несколько.

Оказывается, что для любой сети величина максимального потока совпадает с пропускной способностью минимального разреза. Этот результат был получен американскими математиками Фордом и Фолкерсоном в 1955 году. Мы приведем его доказательство, однако прежде отметим ряд вспомогательных фактов.

Если j - поток через сеть N=(G,a), то через G_j будем обозначать суграф графа G, содержащий дуги, по которым проходит ненулевой поток (и только такие дуги).

Лемма 1. Для любого потока j через сеть N=(G,a) существует поток j через ту же сеть такой, что ½j½=½y½ и G_y - бесконтурный подграф графа G_j.

Доказательство. Предположим, что граф G_j содержит контур С, проходящий по дугам е₁,е₂,…,е_l. Среди чисел j (e₁), j(e₂), …, j (e_l) выберем наименьшее, пусть это будет число m. Рассмотрим функцию θ:E®NÈ{0}, определяемую следующим образом:

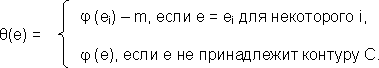
Легко проверить, что θ – поток через сеть N, ½j½= ½θ½ и G_θ – подграф графа G_j. Граф G_θ уже не содержит контура С. Повторяя эту процедуру необходимое число раз, в итоге получаем необходимый поток y.

Лемма доказана.

Лемма 2. Пусть j - ненулевой поток через сеть N с источником а и стоком b. Тогда существует простой (a,b) – путь, проходящий по дугам с ненулевым потоком.

Доказательство. В силу леммы 1 можно считать, что граф G_j = (V,E_j) не содержит контуров. Пусть V_a – множество вершин графа G_j, достижимых из вершины а. Поскольку граф G_j не содержит контуров, то множество V_a содержит хотя бы одну вершину х, которая является стоком в графе G_j. Ясно, что х¹а. Если х¹b, то в графе G существуют дуги с ненулевым потоком, заходящие в х, и не существует дуг с ненулевым потоком, выходящих из х. Это противоречит определению потока. Следовательно, bÎV_a, т.е. в графе G_jвершина b достижима из а. Это означает, что в сети N существует простой (a,b) – путь, проходящий по дугам с ненулевым потоком.

Лемма доказана.

Лемма 3. Величина любого потока через сеть не превосходит пропускной способности любого разреза этой сети.

Доказательство. Пусть j - поток через сеть N=(G,a), S – разрез этой сети. Напомним, что величину потока мы обозначаем через ½j½ а пропускную способность разреза – через a(S).

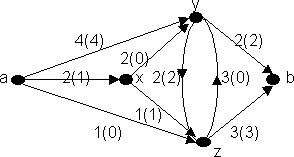
Предположим вначале, что функция j принимает целочисленные значения. Исходя из сети N и потока j, построим орграф G’ с кратными дугами. Множество вершин графа G’ совпадает с множеством вершин исходного графа G. Если е – (x,y)–дуга графа G и j(е)>0, то в графе G’ изображаем j (е) дуг, исходящих из х и заходящих в y. Если же j(е) = 0 или в G нет дуги из х в y, то в G’ тоже нет дуги из х в y. На рис. 6.20 изображен граф G’, построенный для сети N и потока (в скобках), представленных на рис. 6.19.

Рис. 6.19

Рис. 6.20

Из леммы 2 следует, что в графе G’ найдется множество Р из ½j½ простых (a,b)-путей, никакие два из которых не содержат общей дуги. Обозначим через S’ множество дуг графа G’, которые получились из дуг разреза S. Ясно, что S’ - разрез графа G’ и что количество дуг в S’ меньше или равно a(S). Каждый из путей множества Р содержит хотя бы одну дугу из S’, причем два различных пути не могут содержать одну и ту же дугу из S’. Это означает, что число путей в Р не превосходит число дуг в S’, т.е. ½j½=½Р½£½S’½£a(S).

Рассмотрим теперь случай, когда функция j принимает рациональные значения. Пусть m – наибольшее общее кратное всех знаменателей значений функции j. Тогда функция m·j будет потоком в сети (G; m·a). Ясно, что множество S будет разрезом и в новой сети с пропускной способностью, равной m·a(S). В предыдущем абзаце было доказано, что ½m·j½£ m·a(S). Отсюда следует неравенство ½j½£a(S).

Общий случай, т.е. когда допускаются любые значения пропускных способностей и потоков, сводится к рассмотренному выше с помощью следующего утверждения. Для любой сети N=(G,a) с потоком j и разрезом S и любого числа e >0 существует рациональный поток j₀ через ту же сеть, такой что - e <½j½–½j₀½<e и ½j₀½£ a(S).

Лемма доказана.

Для дальнейшего введем ряд обозначений. Пусть N=(G,a) – сеть, имеющая источник а и сток b, D – множество вершин сети, такое, что aÎD, bÏD. Тогда множество ребер

{(u,v) ÎE½uÎD, vÏD}

обозначим через S_D. Легко проверяется, что множество S_D является разрезом сети. Этот разрез будем называть D–разрезом. Если X и Y – непустые множества вершин сети, а j- поток через сеть, то

j (X,Y)=S{ j(u,v)½uÎX, vÎY}.

Например, для сети, изображенной на рис. 6.19, если D={a,x,y}, X={a,x}, Y={x,y,b}, то S_D={(a,z), (x,z), (y,b)}, j (X,Y)= j (a,x)+ j (a,y)+ j (x,y)=1+2+0=3.

Лемма 4. Пусть N=(G,a) – сеть, имеющая источник a и сток b, j - поток через эту сеть, D – множество вершин сети, содержащее a и не содержащее b. Тогда

½j½=j(D,) - j(D,).

Доказательство. По определению потока для x¹a и x¹b имеем равенство

j (x,V) - j (V,x)=0,

а по определению величины потока – равенство

j (a,V) - j (V,a)=½j½.

Из этих равенств следует, что

½j½= (j (x,V) - j (V,x)) = j (D,V) - j (V,D).

Далее, поскольку j(X₁ÈX₂,Y)=j(X₁,Y)+j(X₂,Y) для X₁ÇX₂=Æ и j (X,Y₁ÈY₂)= j(X,Y) + j(X,Y₂) для Y₁ÇY₂=Æ, то j(D,V) - j(V,D) = j(D,DÈ) - j(DÈ,D)=j(D,D)+j(D,) - j(D,D) - j(,D)=j(D,) - j(,D).

Лемма доказана.

Теорема Форда-Фалкерсона. В любой сети величина максимального потока равна пропускной способности минимального разреза.

Доказательство. Пусть j - максимальный поток в сети N=(G,a). В силу леммы 3 достаточно доказать существование разреза S такого, что a(S)=½j½.

Можно считать, что G_j - бесконтурный граф (см. лемму 1).

Дугу e назовем насыщенной, если j(e)=a(e). Обозначим буквой D множество вершин сети, содержащее сток a и все вершины u, для которых существует последовательность

a=x₀, x₁,…, x_k-1, x_k=u,

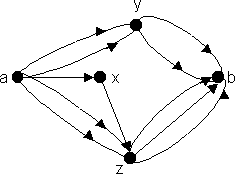
такая, что дуга (x_i, x_i+1) ненасыщенна или через дугу (x_i+1, x_i) проходит ненулевой поток. Например, для сети, изображенной на рис. 6.21. D={a,y,z}. Отметим, что zÎD, хотя дуги (y,z) в сети нет.

Докажем, что bÏD. Предположим, что это не так, т.е. bÎD. Тогда существует последовательность вершин

a=y₀,y₁,…,y_l-1,y_l=b                             (*)

указанного выше вида (т.е. либо дуга (y_i,y_i+1) ненасыщенна, либо через дугу (y_i+1,y_i) проходит ненулевой поток). Пусть e - положительное число, которое меньше разности a(e) - j(e) для любой ненасыщенной дуги e и меньше любого ненулевого потока через дуги сети.

Изменим значение потока j на дугах цепи следующим образом. Если дуга (y_i,y_i+1) ненасыщенна, то положим j'( y_i+1,y_i+1) = j(y_i,y_i+1)+e. Если же эта дуга насыщена, то пустьj'(y_i+1,y_i) = j(y_i+1,y_i)-e. Для остальных дуг e значение потока оставим прежним: j ′(e) = j (e).

Нетрудно убедиться, что j′ - поток через сеть N. Действительно, ограничение j′(e) £ a(e) выполняется для любой дуги e по построению j′. Если через вершину v не проходит цепь (*), то суммарный поток через v равен нулю, поскольку это справедливо для j. Пусть v=y_i для некоторого iÎ{1,…,l-1}. Возможны четыре случая определяемые насыщенностью или ненасыщенностью дуг (y_i-1,y_i) и (y_i,y_i+1). (Нам будет удобно отсутствующую дугу считать насыщенной) Рассмотрим только один из них: дуга (y_i-1,y_i) ненасыщенна, а дуга (y_i,y_i+1) насыщена. Обозначим буквой А множество вершин, из которых выходят дуги, заходящие в y_i, буквой B множество вершин сети, в которые заходят дуги, выходящие из y_i. Тогда

j(x,y_i) = j(y_i,z),                               (**)

поскольку j - поток. При переходе от j к j′ слагаемые в правой части не изменятся, а в левой изменятся два слагаемых: j(y_i-1,y_i) заменятся на j(y_i-1,y_i) + e, а j(y_i+1,y_i) - наj(y_i+1,y_i) - e, но вся сумма останется прежней. Следовательно, равенство (**) сохранится и при переходе от j к j′. Мы доказали, что j′ - поток через сеть N. Но его величина равна ½j½+ e, что противоречит максимальности потока j. Таким образом, bÏD.

Если uÎD и существует дуга, заходящая в u из вершины v, с ненулевым потоком, то vÎD. Это означает, что j(,D)=0. Рассмотрим разрез S_D. Тогда из леммы 4 следует, что½j½=a(S_D), поскольку a(S_D)= j(D, ).

Теорема доказана.

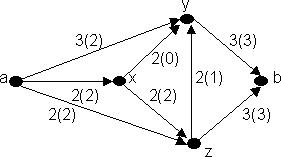
Рис. 6.21

Поскольку на чертеже разрез сети построить проще, чем найти поток через сеть, то теорему Форда-Фолкерсона в случае простых сетей можно использовать для нахождения максимальных потоков в сети. Однако для более-менее сложной сети, даже если найдена величина максимального потока, сам поток построить трудно. Приведем поэтому алгоритм, решающий задачу построения максимального потока для сетей с целочисленными пропускными способностями. Отметим, что в процессе работы алгоритма могут возникать сети, в которых нет ни источника, ни стока.