11-11-2014_20-08-13 / ЗАНЯТИЕ 11 Дифференциальные уравнения_1

1

ЗАНЯТИЕ 18

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

Теоретическая часть:

1.Какое уравнение называется дифференциальным?

2.Порядок дифференциального уравнения.

3.Общий вид дифференциального уравнения.

4.Решение дифференциального уравнения.

5.Понятие начальных условий. Задача Коши.

6.Дифференциальные уравнения 1 порядка.

7.ДУ с разделяющимися переменными.

8.Дифференциальные уравнения 2 порядка.

9.Решение дифференциальных уравнений второго порядка понижением степени.

10.Решение ОЛДУ 2 порядка с постоянными коэффициентами.

Практическая часть:

Найти общее (частное) решение уравнений:

1.Найти частное решение дифференциального уравнения

x2 1 dx 3y 2 dy 0, y 0 1.

Решение:

Данное уравнение является уравнением с разделяющимися переменными. Перенесем второе слагаемое в правую часть уравнения: x2 1 dx 3y 2 dy.

В левой части равенства находится функция, зависящая только от переменной y, в правой – только от x.

Проинтегрируем обе части:

x2 1 dx 3y 2 dy;

x2dx dx 3 ydy 2 dy;

Значит, частное решение дифференциального уравнения будет иметь вид:

2. Найти общее решение дифференциального уравнения x2 y 2y dy xy2 3x dx 0

Решение:

Данное уравнение является уравнением с разделяющимися переменными.

Перенесем второе слагаемое из левой части в правую: x2 y 2y dy xy2 3x dx.

Вынесем за скобки общие множители в правой и левой части равенства: y x2 2 dy x y2 3 dx.

2

Проанализируем получившиеся выражения: в левой части стоит dy. Поэтому в левой части получим функцию, зависящую только от переменной у. В этом случае необходимо разделить обе части уравнения на x2 2 .

В правой части уравнения находится dx, следовательно, необходимо разделить на y2 3 ,

для того, чтобы получилась функция, зависящая только от переменной х.

Таким образом, разделим обе части на x2 2 y2 3 :

x2 2 y2 3 x2 2 y2 3

В левой части равенства находится функция, зависящая только от переменной y, а в правой – только от переменной x. Проинтегрируем обе части:

Вычислим интеграл, стоящей в левой части. Для этого необходимо сделать замену переменных:

Аналогично для интеграла, стоящего в правой части:

Подставим полученные интегралы в уравнение:

Домножим обе части уравнения на 2:

ln y2 3 ln x2 2 lnC.

Перенесем оба логарифмические выражения в левую часть:

ln y2 3 ln x2 2 lnC.

Воспользуемся свойством логарифма (lna lnb ln a b ):

ln 1 y2 x2 1 lnC .

Тогда

y2 3 x2 2 C ;

.

3

Таким образом, общим решением дифференциального уравнения будет являться функцияy2 3 x2 2 C , заданная неявно.

Ответ: y2 3 x2 2 C .

3. Найти частное решение дифференциального уравнения y 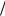x y, y 4 1.

Решение:

Данное уравнение является уравнением с разделяющимися переменными.

«Разнесем» переменные в разные части от знака равенства. Для этого разделим обе части на y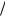x :

Ответ: y e2x 4 .

Найти общие решения уравнений, допускающих понижение порядка:

9. y e 3x

Решение: Данное уравнение второго порядка относится к уравнению вида y f (x). Чтобы найти искомую функцию, необходимо дважды проинтегрировать правую часть уравнения.

Интегрируя первый раз, получим y e 3xdx.

4

Для вычисления этого интеграла нужно сделать замену переменных t 3x:

замену переменных в данном уравнении, получим дифференциальное уравнение первого порядка с разделяющимися переменными

Запишем производную в виде отношения дифференциалов: dp pctgx dx

Умножим обе части равенства на dx: dp pctgxdx.

Чтобы разделить переменные, разделим обе части уравнения на р: dp ctgxdx. p

В левой части равенства находится функция, зависящая только от переменной y, в правой – только от x.

Тогда общее решение имеет вид

ln p ln sinx lnC1

Воспользуемся свойством логарифма (lna lnb ln a b ):

ln p ln C1sinx p C1sinx

Сделаем обратную замену p y , получим y C1 sinx.

Чтобы найти искомую функцию проинтегрируем правую часть уравнения. Тогда y C1 sinxdx C1 sinxdx C1 cosx C2

Ответ: y C1 cosx C2

2

Найти общие решения линейных однородных уравнений второго порядка:

15. Найти общее решение уравнения y 3y 2y 0.

Решение: Данное уравнение является линейным однородным уравнением второго порядка. Для его решения необходимо составить характеристическое уравнение, заменив

y k2, y k, y 1.

Тогда получим квадратное уравнение k2 3k 2 0. Решением этого уравнения являются числа k1 1, k2 2.

Тогда решение дифференциального уравнения будет иметь вид y C1ex C2e2x .

Ответ: y C1ex C2e2x .

16. Найти общее решение уравнения y y 0.

Решение: Составим характеристическое уравнение для уравнения y y 0, заменив

y k2, y k, y 1.