4. Метод трапеций для численного нахождения определенного интеграла: вывод формулы, оценка погрешности, геометрический смысл.

Положим в , n=1, тогда i=(0,1),

Найдем H_i

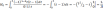
На интервале [x₀,x₁] имеем

Аналогично формулы на остальных интервалах. Суммируя по всем интервалам.

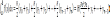(1)

1. – формула трапеций

Оценка погрешности

Предположим, что f(х) дважды непрерывно дифференцируема.

Остаточная часть (погрешность) .

Т.о. R(0)=0.

Найдем R’(h)=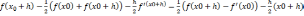 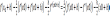(2). Из (2) следует, R’(0)=0.

Найдем R’’(h)=

=

Проинтегрируем R’’(h) на [0,h]

По теореме о среднем, где –некоторая точка из [o,h]

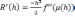
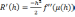(3)

Проинтегрируем (3) на [o,h]

, где принадлежит [o,h]

Суммой по всему отрезку получим

, где M=max, х принадлежит [a,b]

5. Методы численного интегрирования дифференциальных уравнений.

Метод Эйлера

y ^' =f(x,y) (1)

y(x₀)=y_0­ (2) x€[a,b]

Разобьем интервал [a,b] точками x_i, x₀=a, x_n=и, разбиение равномерное.

x_i+1 – x_i = h, проинтегрируем [x₀,x₁], получим

y(x₁) – y(x₀) =

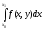
y(x_i) = y_i

Положим, что интервал x_i+1 – x_i достаточно мал, и на интервале функция f(x,y) меняется слабо.

На интервале [x₀,x₁] f(x,y)≈f(x₀,y₀), следовательно y₁=y₀+f(x₀,y₀)(x₁-x₀)

y₁=y₀+h·f(x₀,y₀)

Аналогично на остальных интервалах

y_k+1 = y_k + h·f(x_k,y_k) (3)

k=0…(h-1)

Решение получаем в виде таблицы:

f(x_k,y_k) = y_k^’

y_k+1 = y_k +h·y_k^’ или ∆y_k = h·y_k^’

y_k+1 = y_k + ∆y_k

Оценим погрешность

Используем формулу Тейлора:

y(x₀+h) = y(x₀) + h·y^’(x₀) + O(h²)

Сравнивая с (3), получим:

y₁ = y₀ + h·y^’(x₀) + O(h²), на интервале [x₀,x₁]

Суммарная ошибка умножается на h и общая ошибка O(h)

Геометрическая иллюстрация:

y(x) – точное решение

Формула метода Эйлера

y₁-y₀ = y^’(x₀)(x₁-x₀) – уравнение касательной в точке (x₀,y₀)

Метод Рунге-Кутта

Рассмотрим уравнение (1). Для улучшения точности используем значение функции в промежуточных точках интервалов [x_i,x_i+1]

Предварительно рассчитав некоторые const:

Последующие значения функции находятся по формуле y_i+1 = y_i + ∆y_i,

где ∆y_i =

Доказано, что погрешность этого метода равна O(h⁴).

Принято проводить двойной пересчет для достаточно заданной точности ε, а именно, находим решение с шагом h и 2h и сравниваем их по правилу Рунге.