2.2 Сбор нагрузок на плиту

Нагрузка на 1 м² плиты вычисляется исходя из принятой схемы пола перекрытия. Зная конструкцию перекрытия и вид помещения, определяется нагрузку на 1 м² перекрытия, таблица 1.

Нагрузка на 1м² перекрытия

Таблица 1

Наименование нагрузки и подсчет	Нормативная, кН/м2	Коэффициент надежности по нагрузке γf	Расчетная, кН/м2
Постоянная: Линолеум на мастике δ = 5 мм, γ = 16кН/м3 (0,005•16) Стяжка на цементном растворе δ =20 мм; γ = 20 кН/м3 (0,02•20) Керамзитобетон δ = 50 мм; γ = 15 кН/м3 (0,05•15) Ж/б плита перекрытия δ = 220 мм; g = 3,2 кН/м2 Временная полезная нагрузка: длительная – 0,3 кН/м2 кратковременная – 1,2 кН/м2	0,08 0,4 0,75 3,2 0,3 1,2	1,2 1,3 1,3 1,1 1,3 1,3	0,096 0,52 0,975 3,52 0,39 1,56
Всего	5,93	-	7,06

Полная расчетная нагрузка на 1 погонный метр плиты с номинальным размером ширины 1,5 м равна q = 7,06•1,5 = 10,6 кН/м. С учетом коэффициента γ_п = 0,95

q = 10,6 •0,95 = 10,07 кН/м.

2.3 Определение расчетной схемы плиты

Расчётная схема представляет собой однопролётную балку, загруженную равномерно распределённой нагрузкой интенсивностью q=10,07 кН/м, рисунок 1.

Расчётный пролёт равен расстоянию между центрами площади опирания плиты на стены l₀ = L_н – (а₁+ а₂)/2 = 6000-(200+190)/2=5805 мм, рисунок 2.

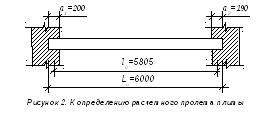
Максимальный изгибающий момент от полной расчетной нагрузки определяется по формуле

М = q l₀²/8, (1)

где q—нагрузка на 1 п.м. плиты, кН/м;

l₀—расчетный пролёт плиты, м.

М = q l₀²/8=10,07•5,805²/8=42,4 кНм.

Максимальная поперечная сила от полной расчетной нагрузки определяется по формуле

Q = q l₀/2= 10,07•5,805/2=29,2 кН. (2)

2.4 Определение расчётного сечения плиты

Пустотная плита приводится к расчётному двутавровому сечению. При изгибе работа бетона в растянутой зоне не учитывается и окончательно принимается тавровое сечение. Круглые пустоты заменяют квадратом со стороной 0,9d, где d—диаметр пустот, рисунок 3.

15 1460 15

0,9d

159

1490

1. Рисунок 3. Поперечное сечение плиты

Толщина полки приведённого сечения определяется по формуле

h_f^’ = (h-0,9 d)/2, (3)

где h - высота приведённого сечения плиты, мм.

h_f^’ = (220-0,9•159)/2=38,5 мм.

Для определения расчетной ширины полки приведённого сечения определятся отношение h_f^’/h. Если h_f^’/h < 0,1, то b_f^’ = 12 h_f^’+b. Если h_f^’/h  0,1, то ширина полки равна ширине плиты. Так как h_f^’/h = 38,5/220 = 0,175 > 0,1, тогда b_f^’=1490 мм, рисунок 4.

Ширина ребра приведённого таврового сечения определяется по формуле

b = b_f^’-n 0,9 d, (4)

где n - число пустот в плите.

b = b_f^’-n 0,9 d = 1490-7•0,9•159 = 488 мм.