Новая папка / № 17

17. Методика изучения бинома Ньютона, свойств разложения бинома, треугольника Паскаля.

1 подход. (а+в), (а+в), (а+в)… замечаем закономерность в составлении многочленов. А уже далее составляют многочлен для (а+в) и получаем общее выражение, которое доказывается ММИ.

2 подход. (а+в)= ( где n-натур.число). Далее доказывается справедливость ММИ.

3 подход. Найдем значение произведения (х+а)(х+в)=х+(а+в)х+ав. Далее (х+а)(х+в)(х+с)=х. Основываясь на этой закономерности, можем записать: (х+а)(х+в)(х+с)…(х+к)(х+р)=. Далее обозначаем суммы при степенях х, начиная от n-1 до 0 соответственно S и заменяем. Тогда получим равенство: . Затем рассмотрим суммы S. Они являются сочетаниями ,…,. Далее вывод, что

()=.

Дидактические преимущества подходов по выводу формулы бинома Ньютона.

1 подход применяется с использованием проблемной ситуацией.

2 подход: используя данный подход, ученики не увидят закономерности в образовании общей формулы бинома Ньютона.

3 подход позволяет ввести понятие бинома Ньютона с помощью совместной поисковой работы учеников и учителя.

Свойства разложения бинома

1. Разложение бинома имеет (m+1) член.

2. Показатель х убывает от m до 0, а показатель а возрастает от 0 до m. Сумма показателей а и х в каждом члене разложения равна m.

3. Второй член ра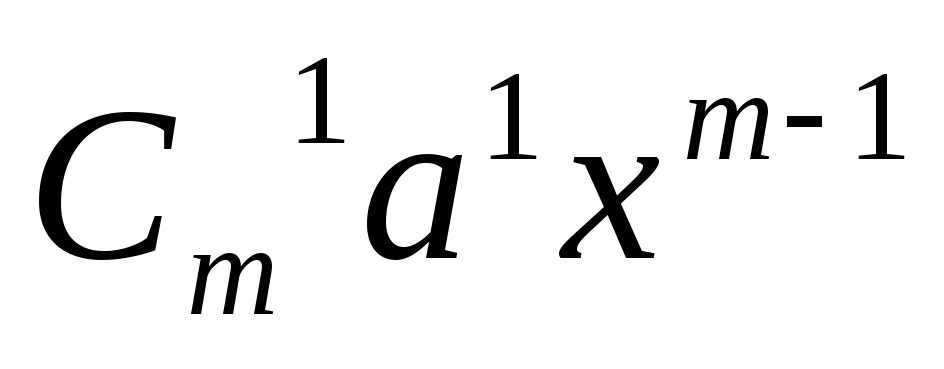вен , третий член равен 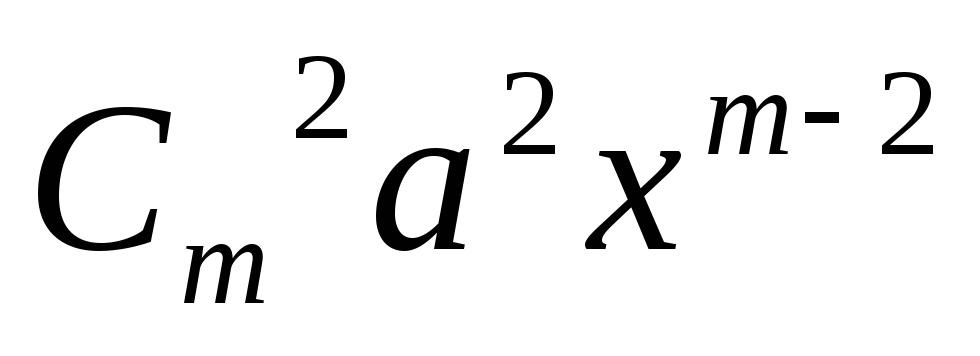, 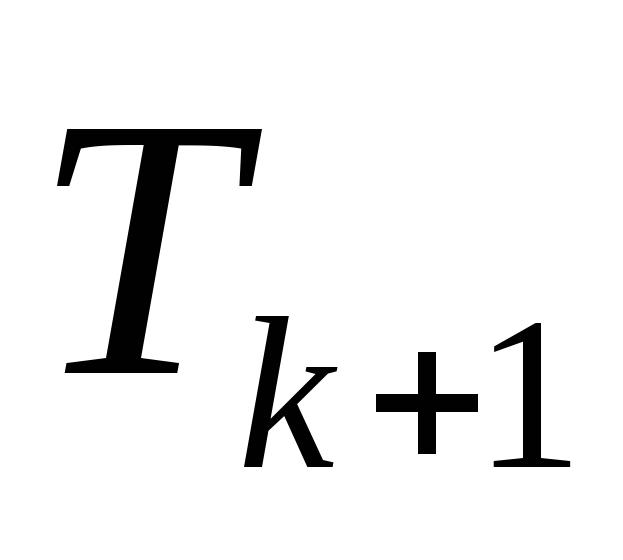=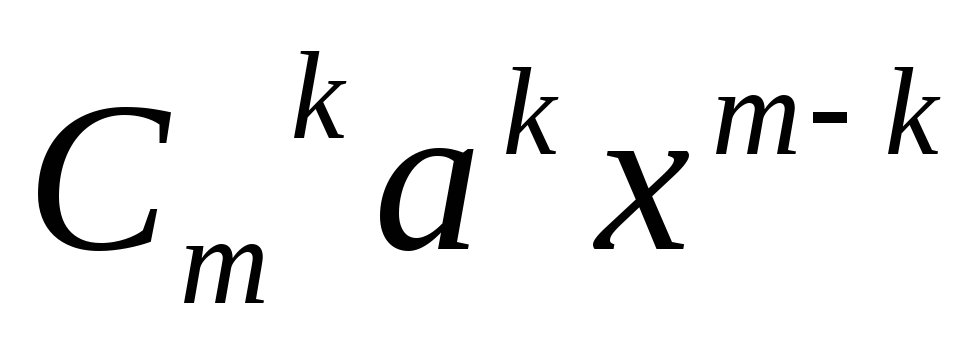-формула любого члена разложения бинома.

4. Коэффициенты …-биномиальные коэффициенты.

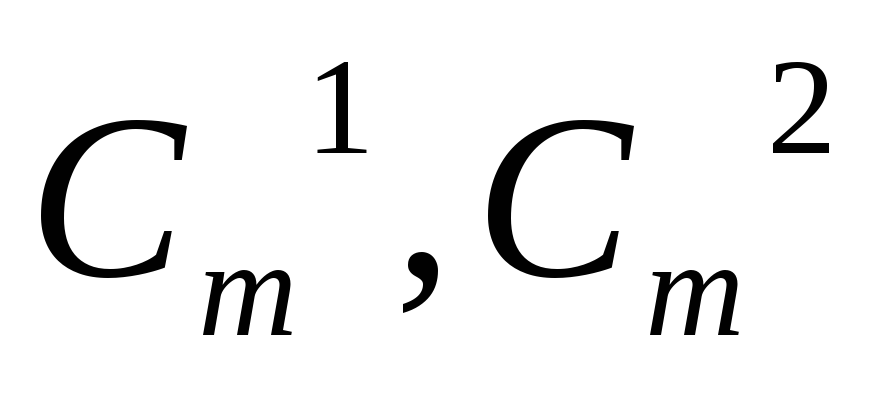5. Биномиальные коэффициенты, равноотстоящие от концов разложения равны между собой.

6. Члены разложения бинома, имеющие наибольший биномиальный коэффициент, называются средним коэффициентом.

а) если показатель число четное- 1 средний член

б) если показатель число нечетное, членов разложения четное, средних членов-2.

треугольника Паскаля

Заполнение каждой строки, начиная с третьей, происходит следующим образом, в соответствии со свойствами сочетаний:

1. Крайние слева и справа элементы любой строки равны 1

2. Каждый внутренний элемент строки равен сумме соседних с ним слева и справа элементов предыдущей строки.

Получаем следующую фигуру (при n=0,1,2,3,4,5)

n=0 1

n=1 1 1

n=2 1 2 1

n=3 1 3 3 1

n=4 1 4 6 4 1

n=5 1 5 10 10 5 1