
Новая папка / № 6
.doc№6 Методика изучения показательной и логарифмической функции в средней школе.
Изучение темы «Показательная функция»
целесообразно начать с пункта «Степень
с иррациональным показателем»:
зафиксировать некоторое положительное
число
![]() и поставив в соответствие каждому числу
и поставив в соответствие каждому числу
![]() число
число
![]() и получить числовую функцию
и получить числовую функцию
![]() ,
определенную на множестве Q.
При а=1 функция постоянна при любом
рациональном
,
определенную на множестве Q.
При а=1 функция постоянна при любом
рациональном
![]() .
.
Далее следует построить график частного
случая, например,
![]() на каком-либо отрезке -
на каком-либо отрезке -
![]() с
определенным шагом -
с
определенным шагом -
![]() .
Уменьшать шаг и привести учащихся к
мысли, что получившиеся точки можно
соединить плавной кривой и считать ее
графиком функции. Следующим шагом будет
построение графика функции
.
Уменьшать шаг и привести учащихся к
мысли, что получившиеся точки можно
соединить плавной кривой и считать ее
графиком функции. Следующим шагом будет
построение графика функции
![]() и убеждение учащихся в том, что она
обладает теми же свойствами, что и
и убеждение учащихся в том, что она
обладает теми же свойствами, что и
![]() .
Учащиеся должны заметить, что функция
.
Учащиеся должны заметить, что функция
![]() - возрастает, а
- возрастает, а
![]() - убывает.
- убывает.
Нужно показать учащимся как определяется
функция
![]() при a>1 показав, что чем
ближе некоторые числа
при a>1 показав, что чем
ближе некоторые числа
![]() и
и
![]() к
к
![]() ,
тем меньше отличаются
,
тем меньше отличаются
![]() и
и
![]() .
По аналогии рассмотреть случай:
.
По аналогии рассмотреть случай:
![]() .
.
Рассмотреть свойства показательной функции (без доказательства или с доказательством – в зависимости от подготовленности учащихся), начав с ее математического определения.
О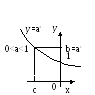 пределение.
Функция, заданная формулой
пределение.
Функция, заданная формулой
![]() ,
где
,
где
![]() и
и
![]() ,
называется показательной функцией с
основанием
,
называется показательной функцией с
основанием
![]() .
.
С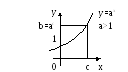 войства:
войства:
-

-
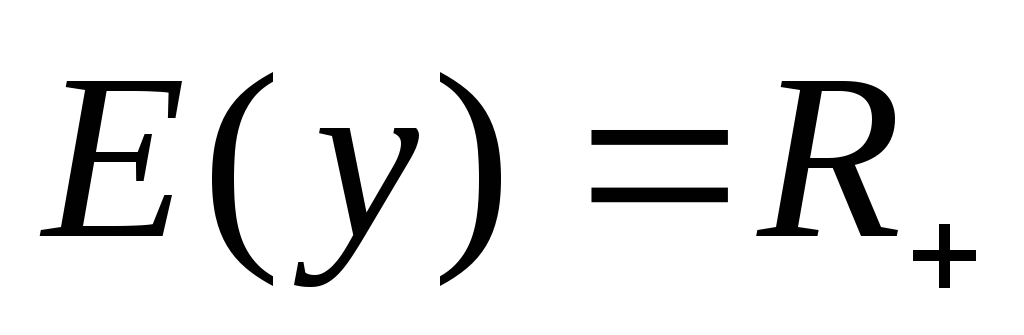
-
При
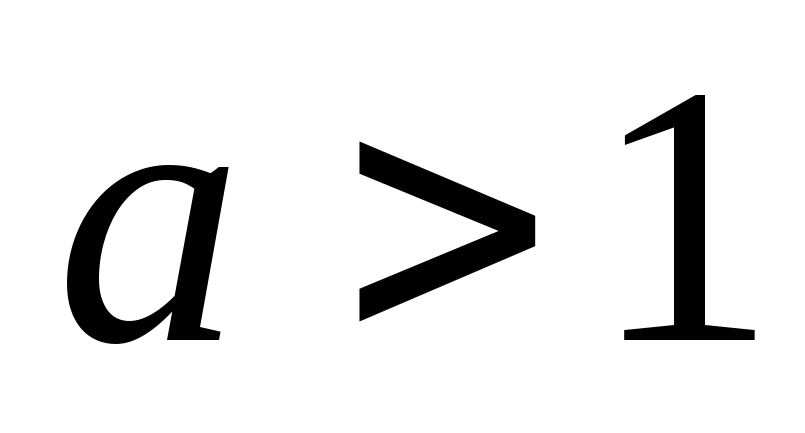 функция возрастает на R,
при
функция возрастает на R,
при
 - убывает.
- убывает. -
При любых
 :
:
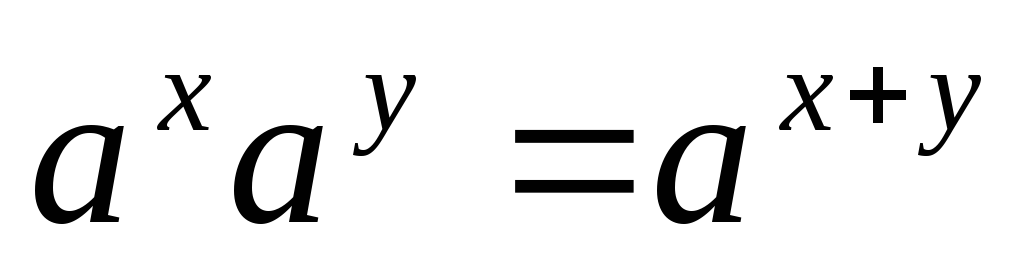 ,
,
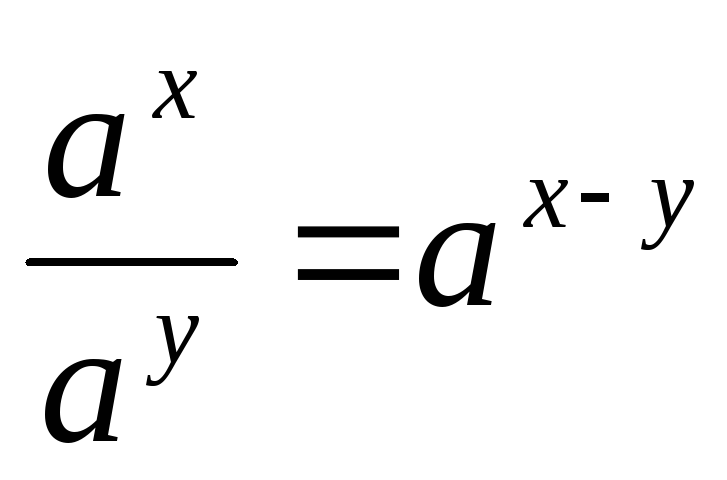 ,
,
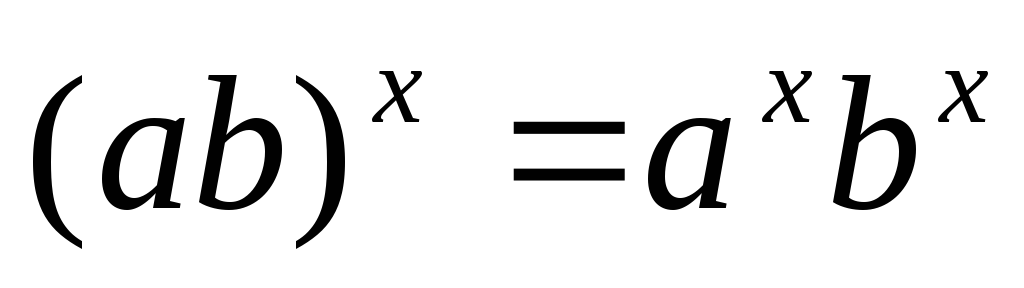 ,
,
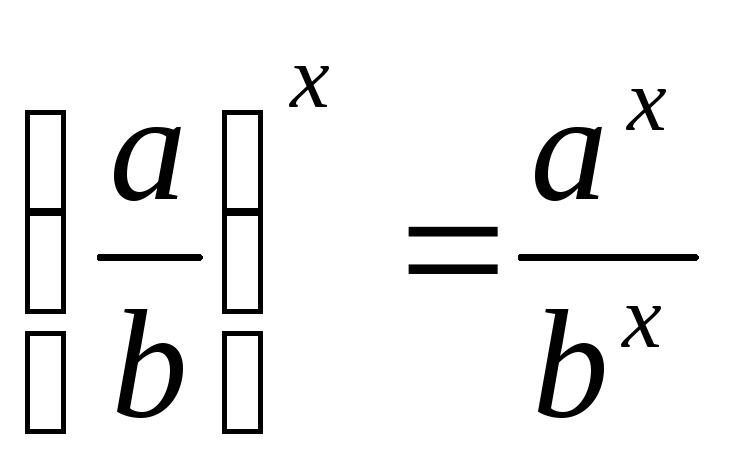 ,
,
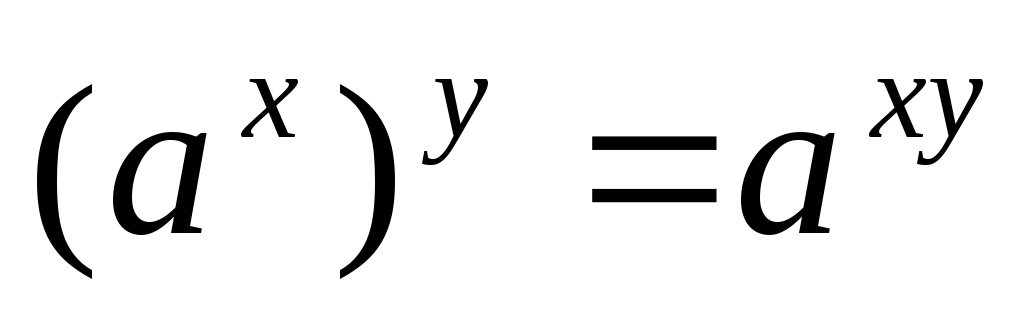 .
.
Типовые задания:
-
Перечислите свойства функции и постройте ее график:
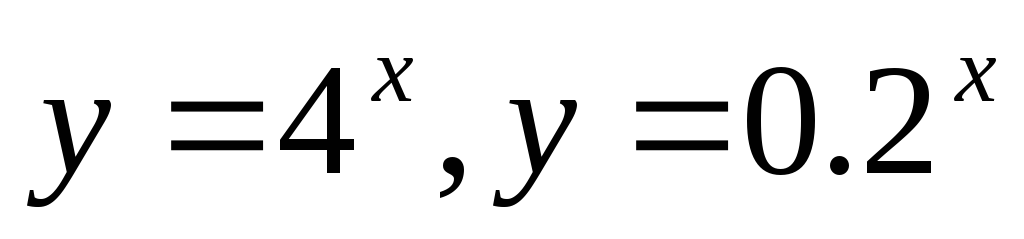 .
. -
Найдите область значения функций:
 .
. -
Сравните числа:
 .
. -
Вычислите:
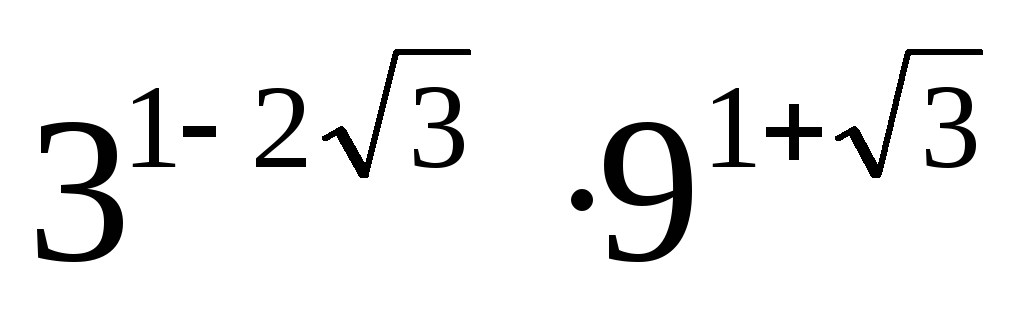 .
. -
Упростите выражение:
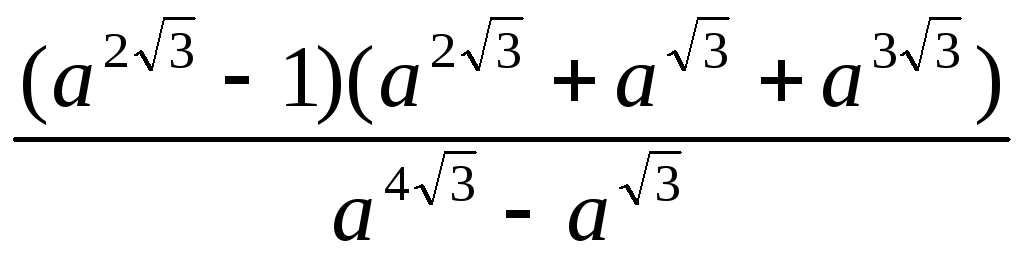 .
. -
Определите, является ли функция возрастающей (убывающей):
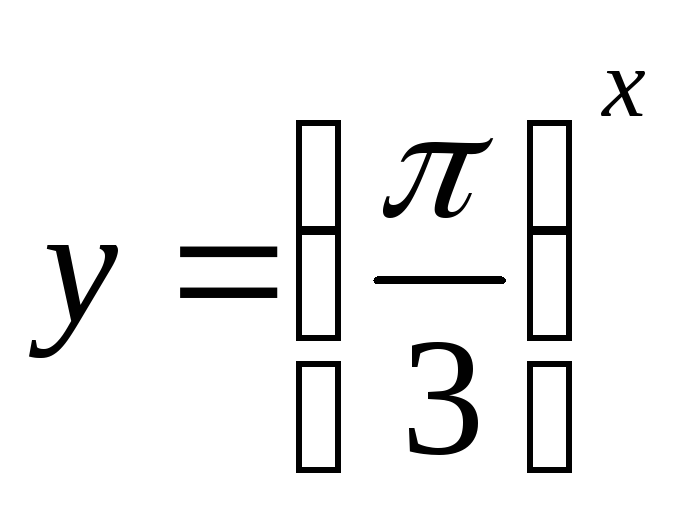 .
. -
Найдите наибольшее и наименьшее значение функции на R:
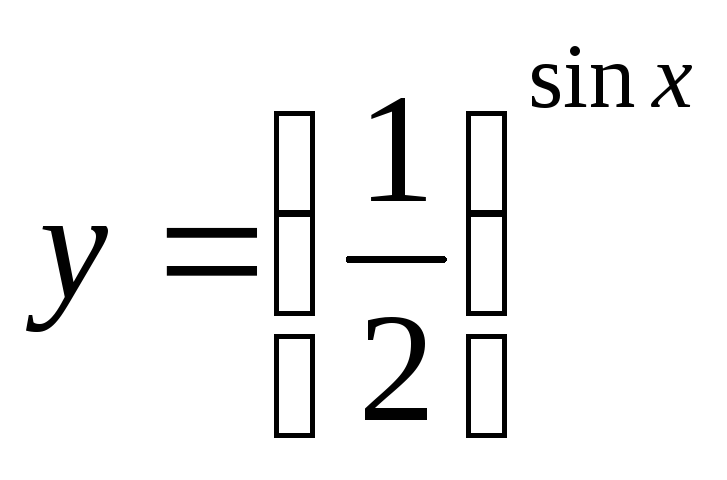
-
Решите графически уравнение:
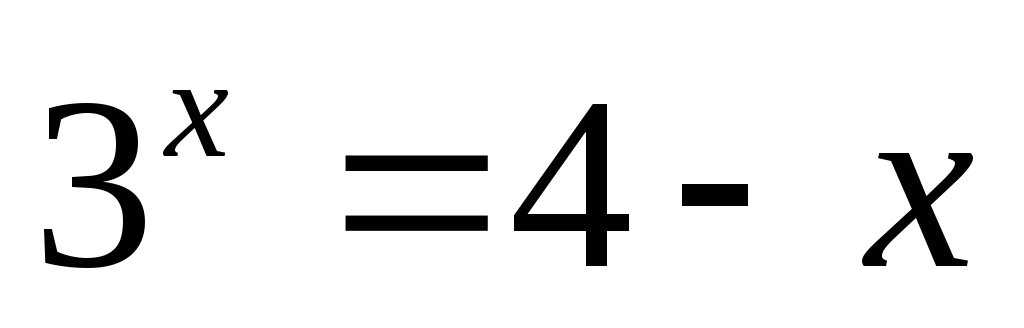
Решение показательных уравнений и неравенств.
Решение показательных уравнений и неравенств основывается на свойствах показательной функции, поэтому при решении упражнений по данной теме систематически проверяются эти свойства.
Для решения систем, содержащих одно или два показательных уравнения, применяются методы подстановки и замены переменных.
Изучение начинается с рассмотрения
простейшего уравнения
![]() ,
,
![]() ,
,
![]() .
Т. к.
.
Т. к.
![]() имеем: если
имеем: если
![]() ,
то уравнение не имеет решений; в случае
,
то уравнение не имеет решений; в случае
![]() если
если
![]() (
(![]() ),
то функция возрастает(убывает) на области
определения и принимает положительные
значения. По теореме о корне имеет
единственный корень. Для того чтобы его
найти, надо
),
то функция возрастает(убывает) на области
определения и принимает положительные
значения. По теореме о корне имеет
единственный корень. Для того чтобы его
найти, надо
![]() представить в виде
представить в виде
![]() .
.
![]() - является решением уравнения.
- является решением уравнения.
Разобрать примеры:
![]() ;
;
![]() .
.
Решение заданий, аналогичных разобранным.
Логарифмы и их свойства
Необходимо вернуться к решению уравнения
![]() ,
,
![]() ,
,
![]() и сказать, что при
и сказать, что при
![]() единственный корень называют логарифмом
числа
единственный корень называют логарифмом
числа
![]() по
основанию
по
основанию
![]() ,
который обозначают
,
который обозначают
![]() .
.
То есть:
![]() .
.
Определение. Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число b.
Формулу
![]() называют основным логарифмическим
тождеством.
называют основным логарифмическим
тождеством.
Отработать понимание учащимися определения логарифма.
Типовые задания:
-
Найдите
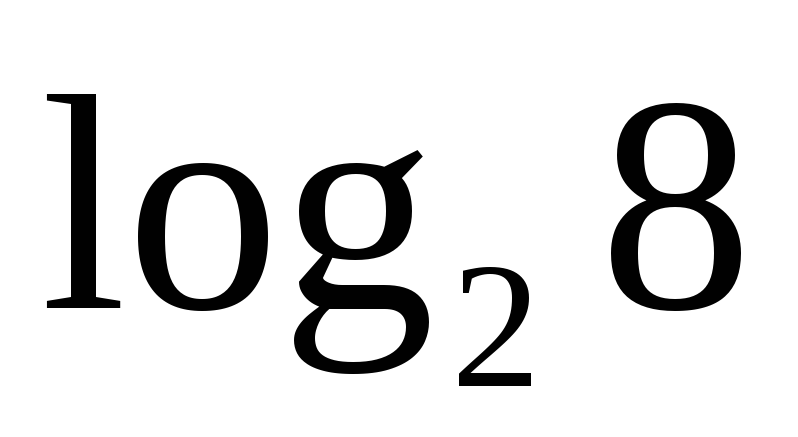 .
. -
Найдите логарифм числа
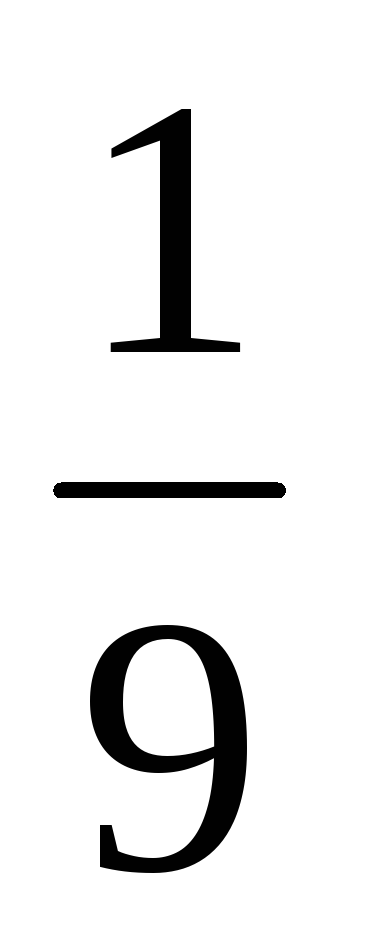 по основанию
по основанию
 .
. -
Найдите
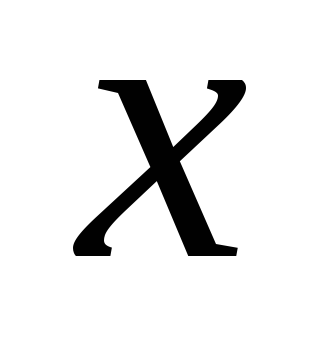 такое, что
такое, что
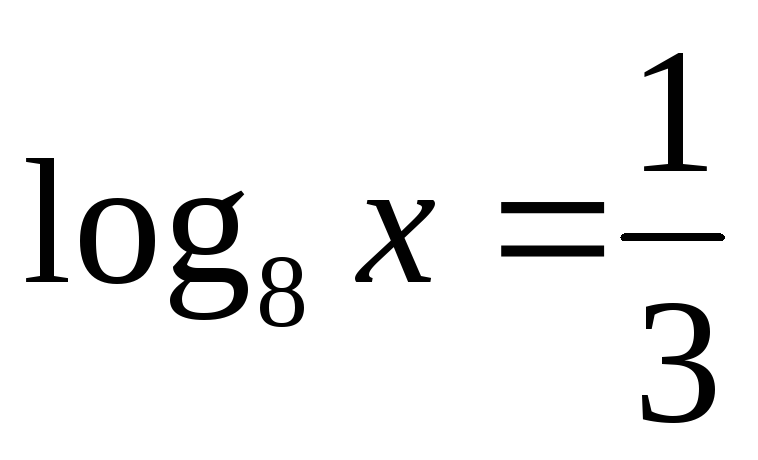 .
.
При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:
Для доказательства (3) и (4) пользуются
основным логарифмическим тождеством
![]() ,
,
![]() :
:
3: Логарифм произведения равен сумме логарифмов.
![]() и по определению логарифма
и по определению логарифма
![]() .
.
4: Логарифм частного равен разности логарифмов.
![]() ,
следовательно по определению логарифма
,
следовательно по определению логарифма
![]() .
.
5: Логарифм степени равен произведению показателя степени на логарифм основания этой степени.
![]() .
Значит по определению логарифма
.
Значит по определению логарифма
![]() .
.
Основные свойства логарифмов широко
применяются в ходе преобразования
выражений, содержащих логарифмы. Далее
целесообразно доказать формулу перехода
от одного основания логарифма к другому:
![]() .
По правилу логарифмирования степени и
основному логарифмическому тождеству
получим:
.
По правилу логарифмирования степени и
основному логарифмическому тождеству
получим:
![]() .
Разделим обе части полученного равенства
на
.
Разделим обе части полученного равенства
на
![]() ,
приходим к нужной формуле.
,
приходим к нужной формуле.
Важно отметить, что логарифмы с
основаниями 10 и e называют
десятичными натуральными соответственно
и обозначают
![]() .
.
Отработать понимание основных свойств логарифмов.
Типовые задания:
-
Известно, что
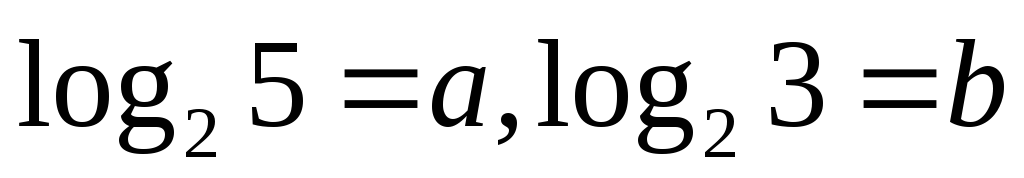 .
Выразите
.
Выразите
 через
через
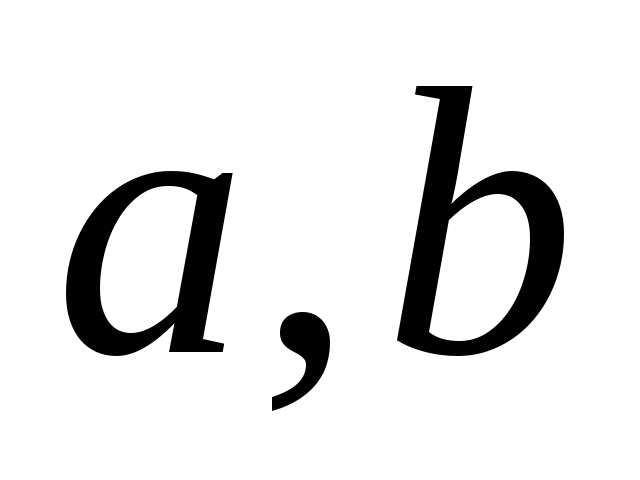 .
. -
Найдите
 ,
если
,
если
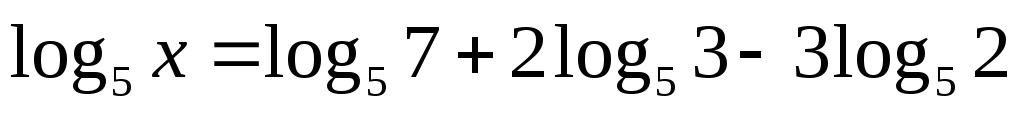 .
. -
Найдите значение выражения
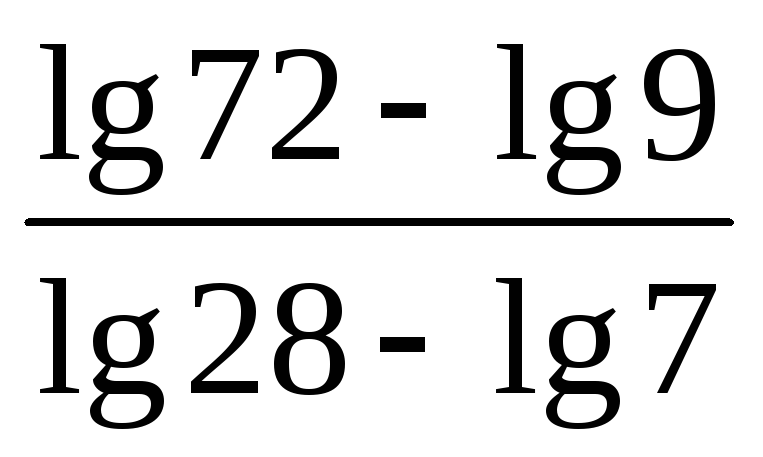 .
.
Логарифмическая функция
Пусть a – положительное число, не равное 1.
Определение. Функцию. Заданную
формулой
![]() ,
называют логарифмической функцией с
основанием a.
,
называют логарифмической функцией с
основанием a.
Свойства.
-
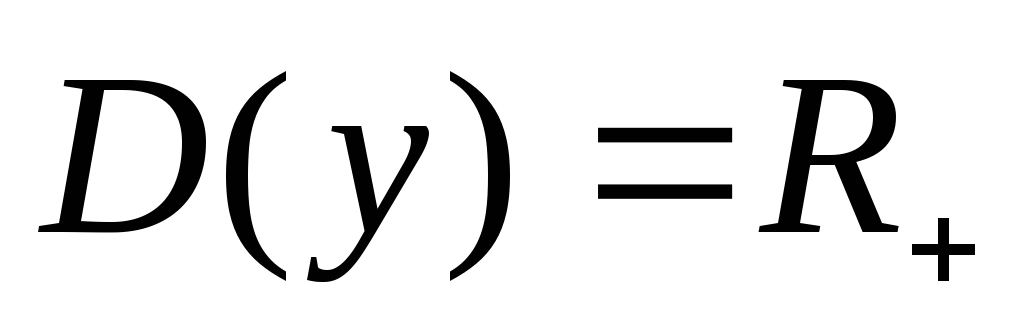
-
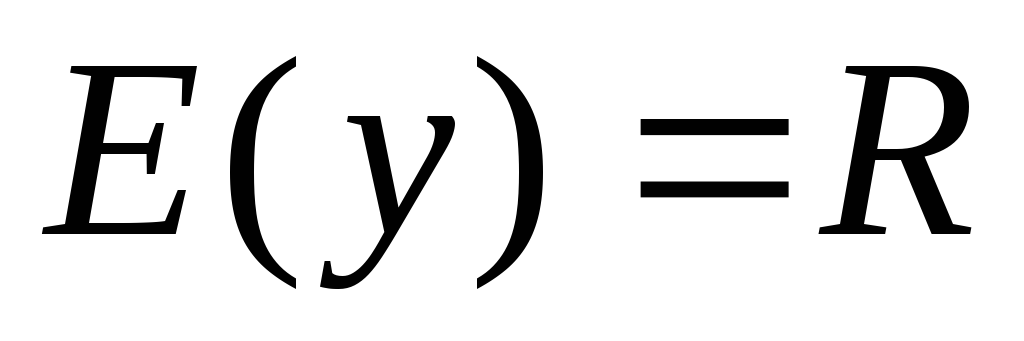
-
Логарифмическая функция на всей области определения возрастает при a>0 и убывает при 0<a<1.
Докажем, что при a>0
функция возрастает. Пусть
![]() - произвольные положительные числа и
- произвольные положительные числа и
![]() .
Надо доказать, что
.
Надо доказать, что
![]() .
Допустим противное
.
Допустим противное
![]() .
Так как функция
.
Так как функция
![]() при a>1 взрастает, то
при a>1 взрастает, то
![]() .
Но
.
Но
![]() ,
т. е.
,
т. е.
![]() - что противоречит условию.
- что противоречит условию.
Для построения графика необходимо заметить:
-
Значение 0 логарифмическая функция принимает точке 1;
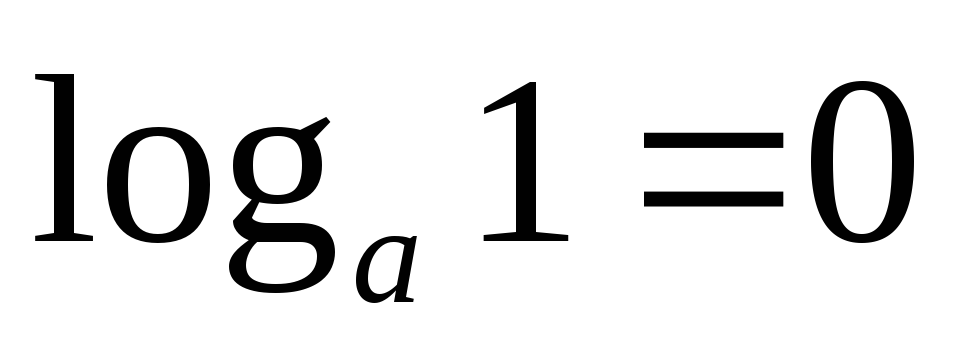 при любом
при любом
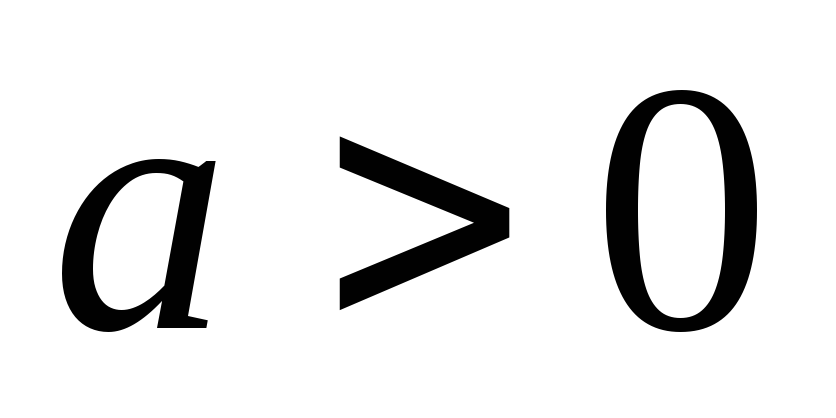 ,
так как
,
так как

-
Вследствие возрастания функции при
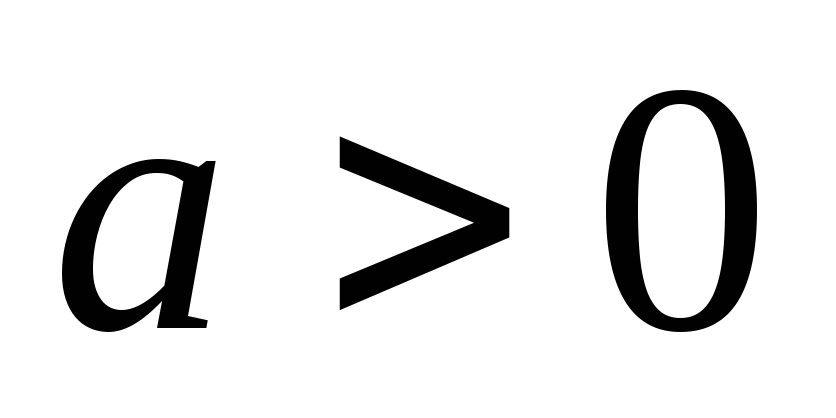 получаем, что при
получаем, что при
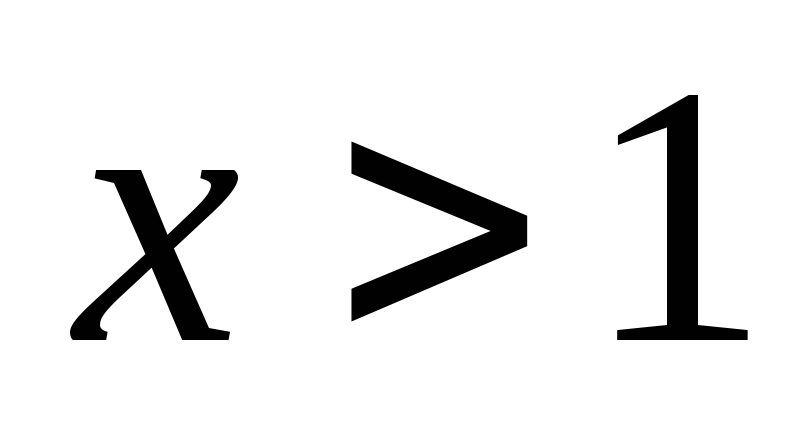 логарифмическая функция принимает
положительные значения, а при
логарифмическая функция принимает
положительные значения, а при
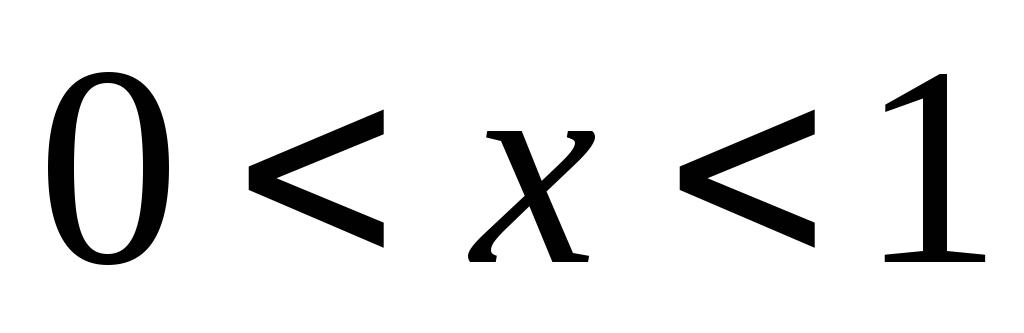 - отрицательные.
- отрицательные. -
Если
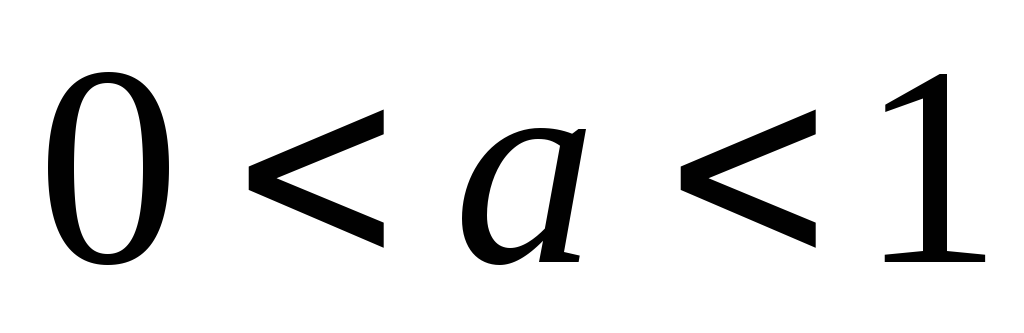 ,
то
,
то
 убывает на
убывает на
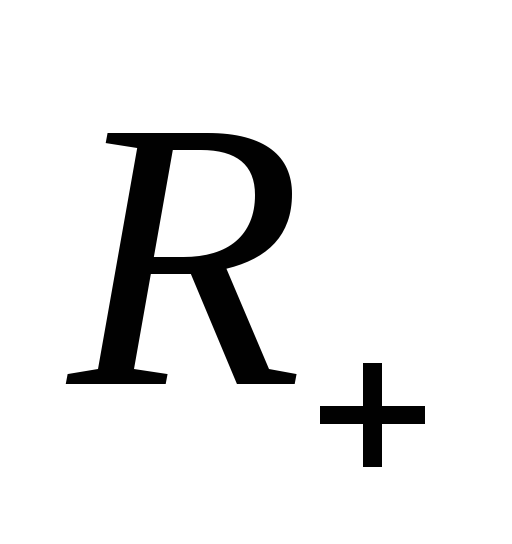 ,
поэтому
,
поэтому
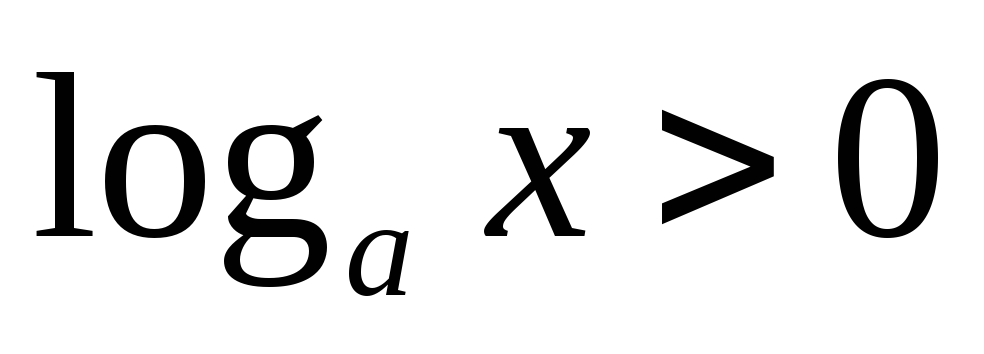 при
при
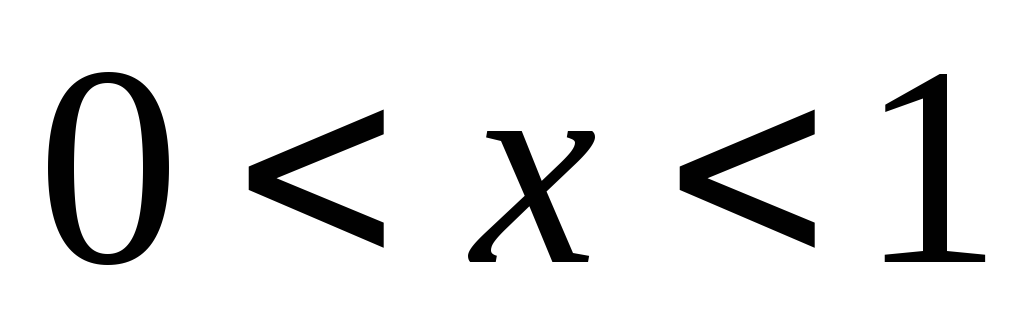 и
и
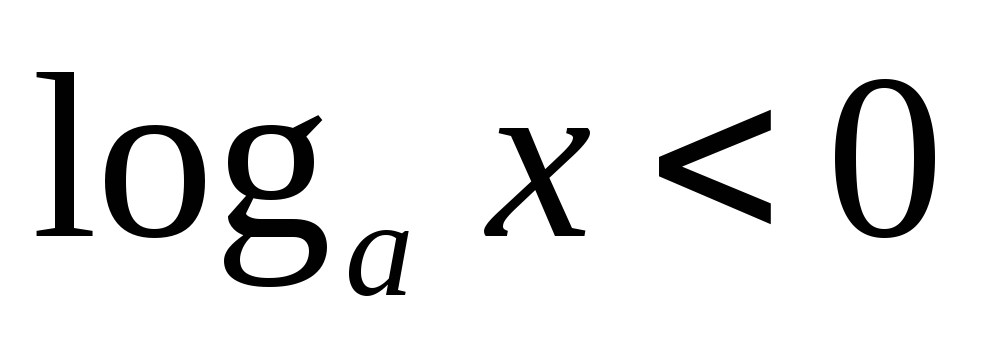 при
при
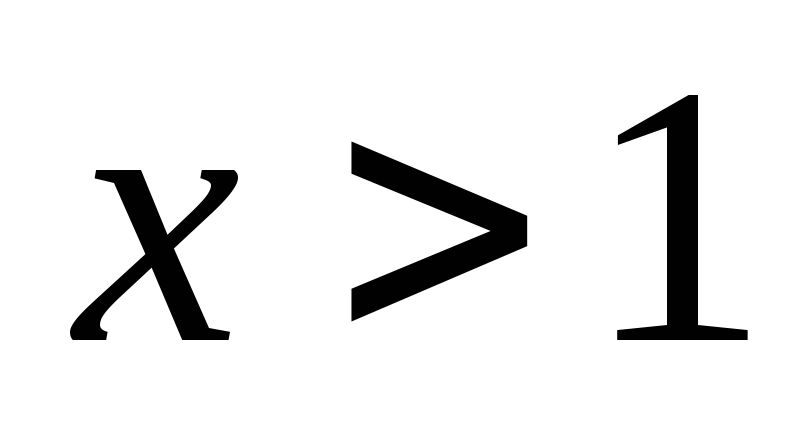
Г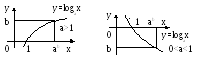 рафики
показательной и логарифмической функции,
имеющих одинаковое основание. Симметричны
относительно прямо y=x.
Отработать
свойства, графики и определение
логарифмической функции.
рафики
показательной и логарифмической функции,
имеющих одинаковое основание. Симметричны
относительно прямо y=x.
Отработать
свойства, графики и определение
логарифмической функции.
Типовые задания:
-
Найдите область определения функции
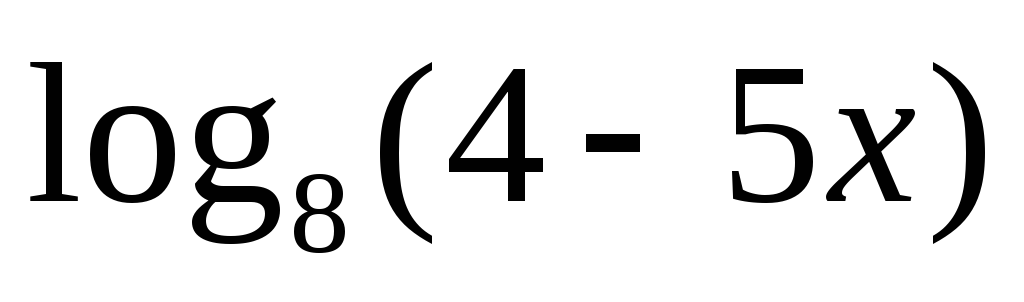 .
. -
Сравните числа:
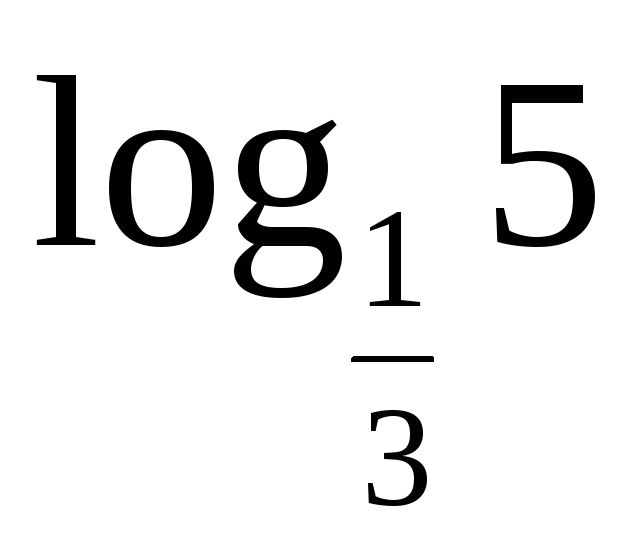 и
и
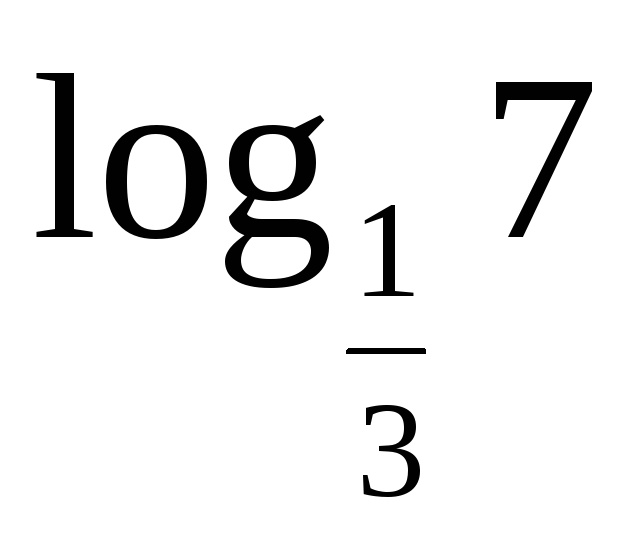 .
. -
Перечислите основные свойства и постройте график функции
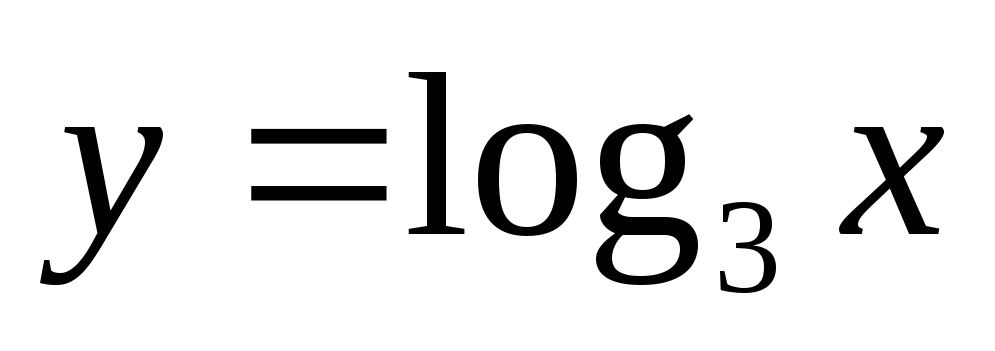 ,
,
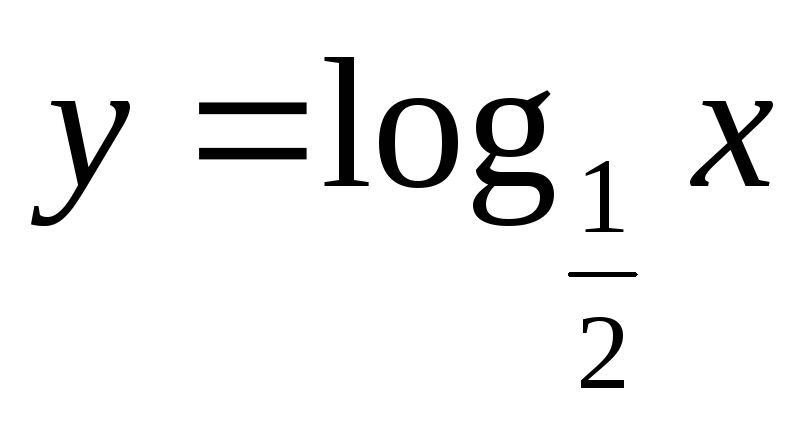 .
.
Решение показательных и логарифмических уравнений
При решении логарифмических уравнений появляется настоятельная необходимость формирования понятий следствия и равносильности.
Изучение пункта начинается с рассмотрения
простейшего логарифмического уравнения
![]() .
Логарифмическая функция возрастает
(или убывает) не
.
Логарифмическая функция возрастает
(или убывает) не
![]() и принимает на этом промежутке се
действительные значения. По теореме о
корне следует, что для любого b
данное уравнение имеет одно и притом
только одно решение. Из определения
логарифма следует, что
и принимает на этом промежутке се
действительные значения. По теореме о
корне следует, что для любого b
данное уравнение имеет одно и притом
только одно решение. Из определения
логарифма следует, что
![]() является таким решением.
является таким решением.
Рассмотреть примеры и отработать решение логарифмических уравнений.
Типовые задания:
-
Решите уравнение
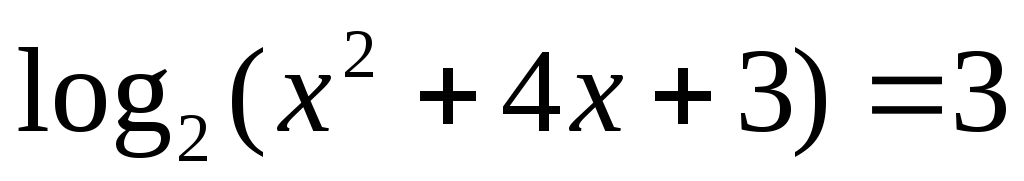 .
. -
Решите уравнение
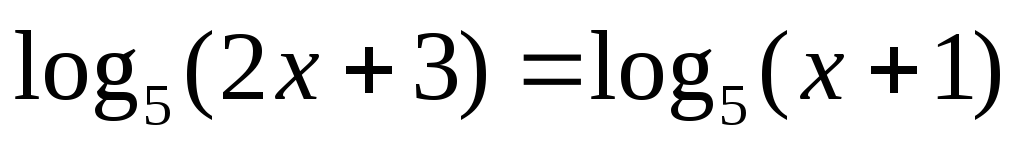 .
. -
Решите уравнение
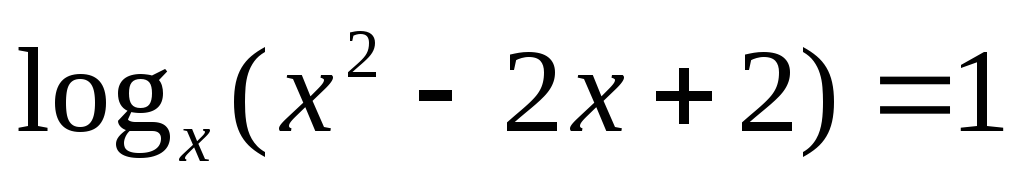 .
. -
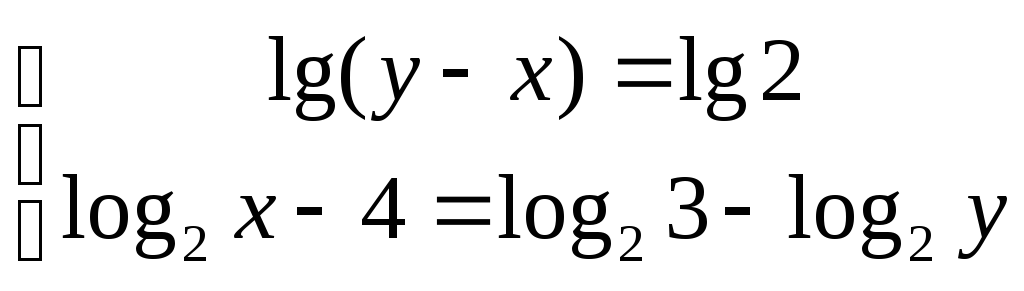 ..
.. -
Аналогичные неравенства.
Понятие об обратной функции.
В ходе исследования различны функций, учащиеся неоднократно встречались с задачами:
-
Вычислить значение функции
 по данному значению
по данному значению
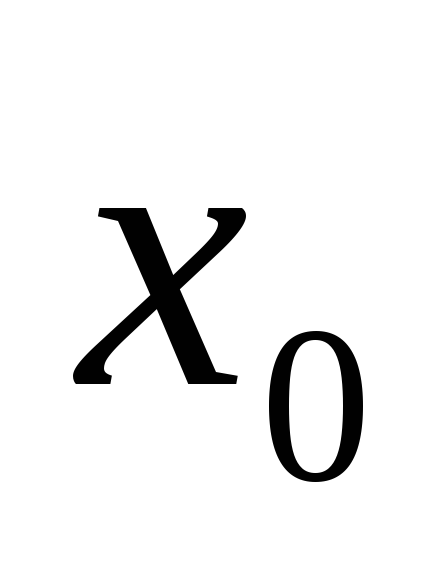 аргумента.
аргумента. -
Найти значения аргумента, при которых функция
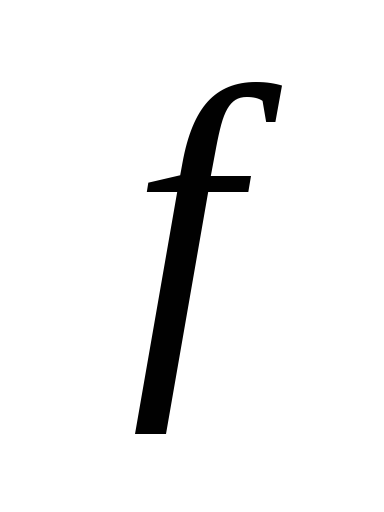 принимает данное значение
принимает данное значение
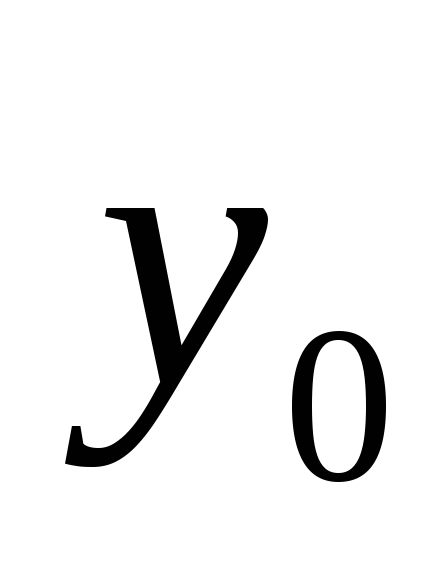 .
.
Разобрать пример: Пусть
![]() .
Чтобы найти значения аргумента
.
Чтобы найти значения аргумента
![]() ,
при которых
,
при которых
![]() .
Надо решить уравнение
.
Надо решить уравнение
![]() ,
т. е. уравнение
,
т. е. уравнение
![]() .
Решая его, находим, что при любом
.
Решая его, находим, что при любом
![]() оно имеет, и при том только одно, решение
оно имеет, и при том только одно, решение
![]() .
.
Важно отметить, что функцию, принимающую
каждое свое значение в единственной
точке области определения, называют
обратимой. Функция
![]() обратима, а функция
обратима, а функция
![]() не является обратимой (При
не является обратимой (При
![]() :
:
![]() ).
).
Пусть
![]() - произвольная обратимая функция. Для
любого числа
- произвольная обратимая функция. Для
любого числа
![]() имеется в точности одно значение
имеется в точности одно значение
![]() ,
такое, что
,
такое, что
![]() .
Поставим в соответствие каждому
.
Поставим в соответствие каждому
![]() значение
значение
![]() ,
тогда получим новую функцию
,
тогда получим новую функцию
![]() с областью определения
с областью определения
![]() и областью значения
и областью значения
![]() .
.
Пример: Докажем, что функция
![]() обратима, и выведем формулу, задающую
функцию
обратима, и выведем формулу, задающую
функцию
![]() ,
обратную к
,
обратную к
![]() .
.
-
Уравнение
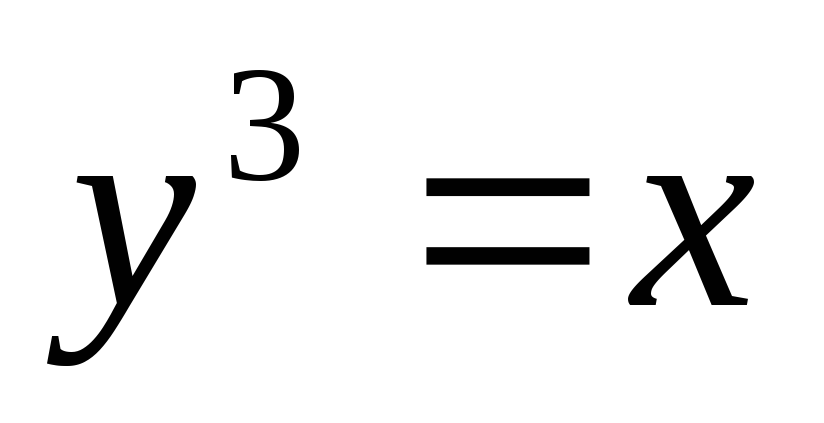 имеет единственное решение
имеет единственное решение
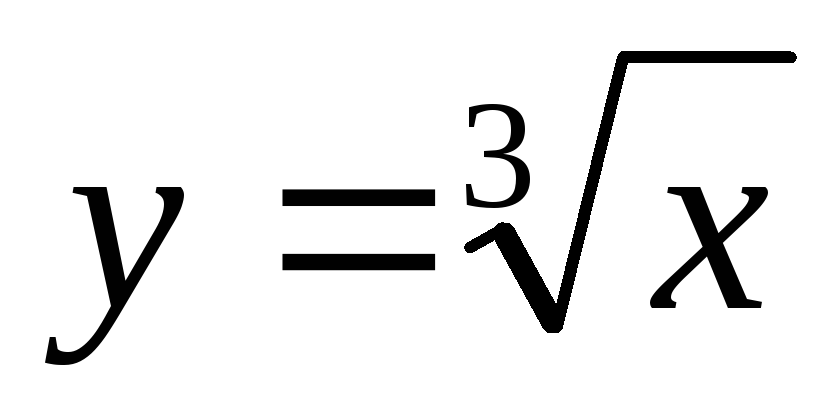 .
. -
Функция
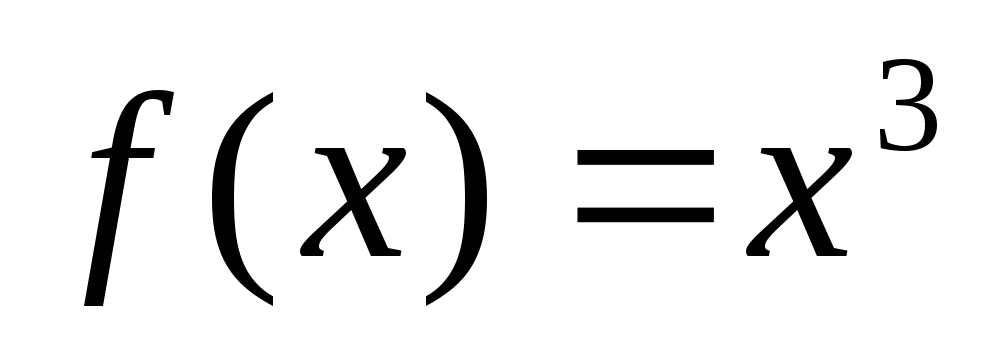 обратима и обратной к ней является
функция
обратима и обратной к ней является
функция
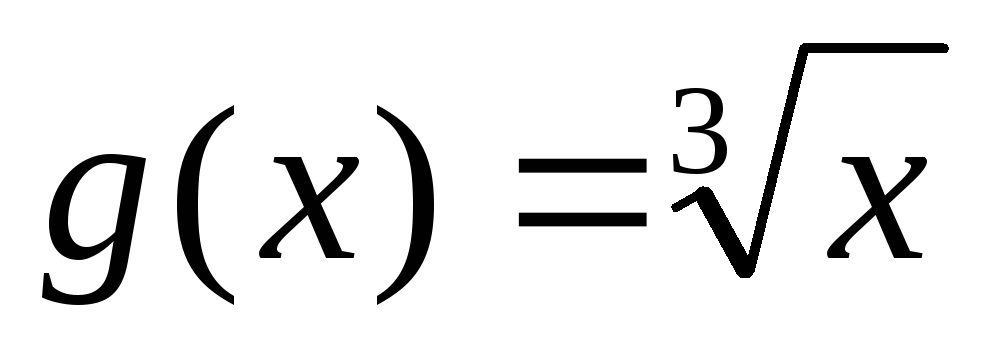 .
.
С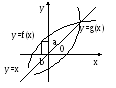 войство
обратных функций: Графики функции
войство
обратных функций: Графики функции
![]() и обратной к ней функции
и обратной к ней функции
![]() симметричны относительно прямой
симметричны относительно прямой
![]() .
.
Доказательство. Заметим, что по графику
функции
![]() можно найти числовое значение обратной
к ней функции
можно найти числовое значение обратной
к ней функции
![]() в произвольной точке
в произвольной точке
![]() .
Для этого нужно взять точку с координатой
.
Для этого нужно взять точку с координатой
![]() на вертикальной оси. Из определения
обратной функции следует, что значение
на вертикальной оси. Из определения
обратной функции следует, что значение
![]() равно
равно
![]() .
.
Для того, чтобы изобразить график
![]() надо отразить график
надо отразить график
![]() относительно прямой
относительно прямой
![]() .
.
Если функция
![]() - обратная к функции
- обратная к функции
![]() .
То функция
.
То функция
![]() обратима и обратной к ней является
функция
обратима и обратной к ней является
функция
![]() .
Поэтому говорят, что функции
.
Поэтому говорят, что функции
![]() взаимно обратные.
взаимно обратные.
Теорема(об обратной функции). Если
функция
![]() возрастает (или убывает)на промежутке
возрастает (или убывает)на промежутке
![]() ,
то она обратима. Обратная к
,
то она обратима. Обратная к
![]() функция
функция
![]() ,
определенная в области значений
,
определенная в области значений
![]() ,
также является возрастающей.
,
также является возрастающей.
Доказательство. Положим для определенности,
что функция
![]() возрастающая. Обратимость функции
возрастающая. Обратимость функции
![]() - очевидное следствие из теоремы о корне.
Поэтому остается доказать. Что функция
- очевидное следствие из теоремы о корне.
Поэтому остается доказать. Что функция
![]() возрастает на множестве
возрастает на множестве
![]() .
.
Пусть
![]() - произвольные значения из
- произвольные значения из
![]() ,
такие, что
,
такие, что
![]() ,
и пусть
,
и пусть
![]() .
По определению обратной функции
.
По определению обратной функции
![]() .
.
Воспользовавшись условием. Что
![]() - возрастающая функция находим, что
допущение
- возрастающая функция находим, что
допущение
![]() приводит к выводу
приводит к выводу
![]() ,
т. е.
,
т. е.
![]() .
Это противоречит условию
.
Это противоречит условию
![]() Поэтому
Поэтому
![]() ,
т. е. из условия
,
т. е. из условия
![]() следует, что
следует, что
![]() .
.
Типовые задания:
-
Выведите формулу, задающую функцию
 ,
обратную к заданной функции
,
обратную к заданной функции
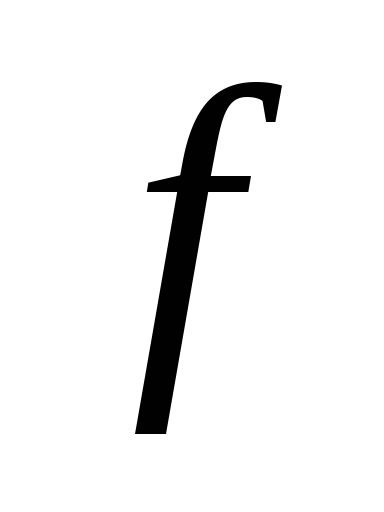 .
Укажите
.
Укажите
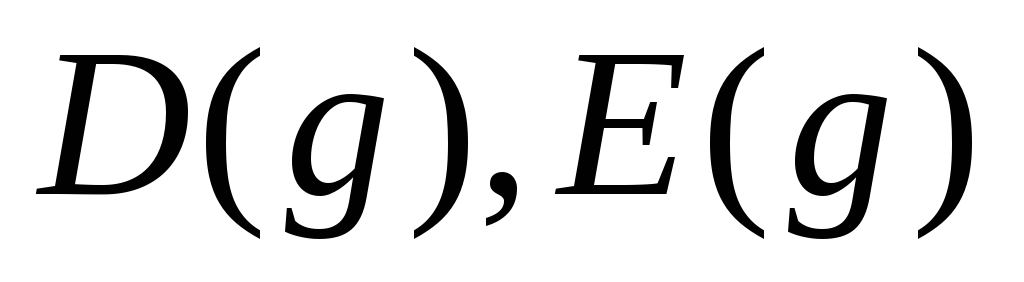 :
:
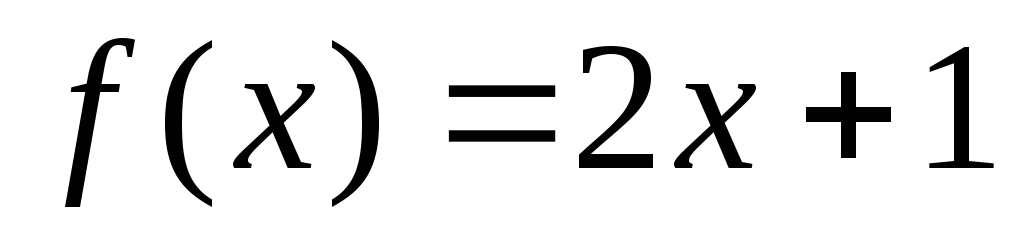 .
. -
Постройте график функции, обратной к
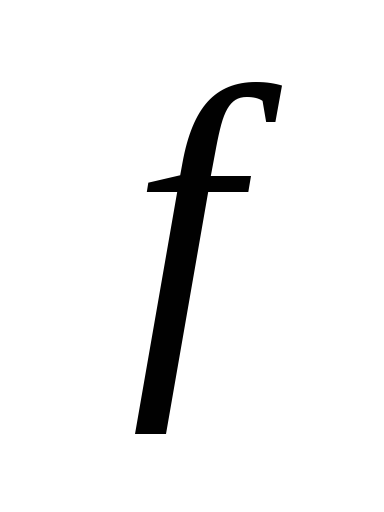 :
:
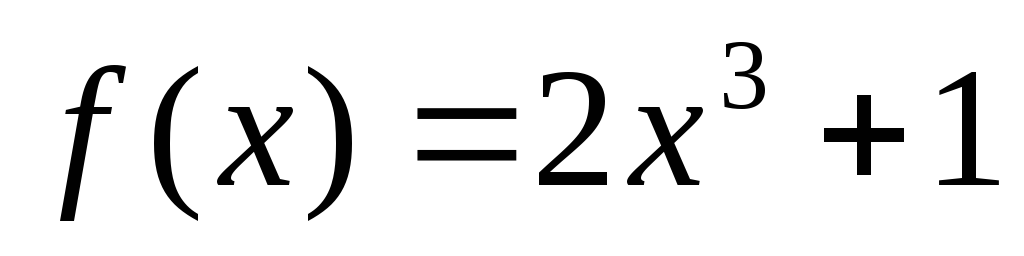 .
. -
Докажите, что функция
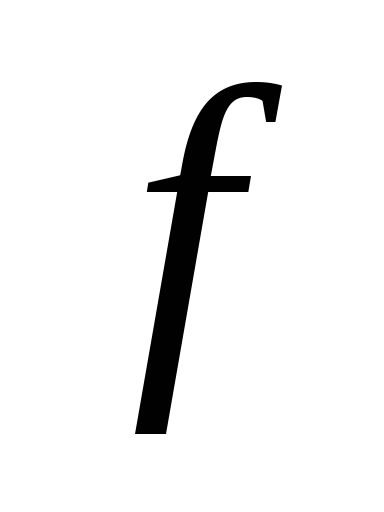 имеет обратную функцию на указанном
промежутке:
имеет обратную функцию на указанном
промежутке:
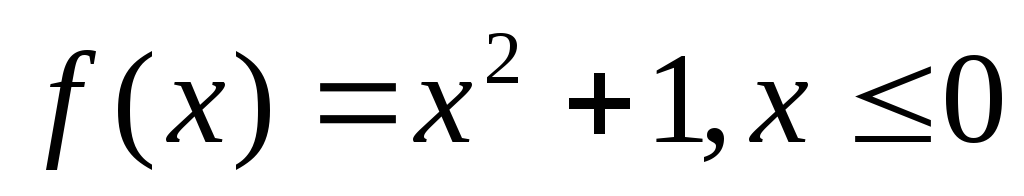 .
.
