3.2. Касательные напряжения. Угол закручивания

Для круглого стержня диаметром d касательные напряжения в произвольной точке поперечного сечения, находящейся на расстоянии ρ от центра сечения, определяются формулой

, (3.4)

где – полярный момент инерции круглого

сечения.

Максимальные касательные напряжения в точках, наиболее удаленных от центра сечения, имеют значение

, (3.5)

где – полярный момент сопротивления круглого сечения. При этом напряжения по сечению изменяются по закону треугольника.

Полный угол закручивания φ на участке стержня длиной l при постоянном крутящем моменте определяется по формуле

, (3.6)

где G – модуль сдвига, МПа.

Если стержень имеет несколько участков, в пределах которых изменяется по тому или иному закону, то полный угол закручивания (угол взаимного поворота концевых сечений стержня) определяется из выражения

. (3.7)

Интегрирование выполняется по длине каждого участка, а суммирование – по всем участкам стержня.

Для валов, у которых нет неподвижных сечений, для построения эпюры угловых перемещений принимают какое-либо сечение за условно неподвижное. Например, углы закручивания удобно отсчитывать в обе стороны от сечения, к которому подводится мощность.

3.3. Расчеты на прочность и жесткость

При кручении размеры сечения для стержня постоянного поперечного сечения подбираются из условия прочности по расчетной формуле

, (3.8)

где maxT_k – наибольший крутящий момент по абсолютному значению.

Если дополнительно ставится условие жесткости φ_max ≤[ φ ] , то подобранное сечение проверяется на жесткость согласно выражению

,

где [φ] – допускаемое значение для угла закручивания;

–расчетная длина, для которой задан допускаемый угол закручивания.

В том случае, когда допускаемый угол закручивания задан в градусах, при подстановке в формулу (3.3) его следует перевести в радианы.

3.4. Построение эпюр т и φ

Пример. Из условия прочности и жесткости определить диаметр вала при заданном расположении зубчатых колес для съема мощности N₂, N₃, N₄. Подводимая мощность – N₁ (рис. 3.1) . принять допускаемое напряжение равным [τ] = 30 Н/мм², G =0,8 10⁵ Н/мм² при допускаемом угле закручивания φ на 1 м длины вала – [φ] = 0,25 град/м; N₁ = 90 кВт; N₃ = 30 кВт; N₄ = 20 кВт; n=250 об/мин. Построить эпюры крутящих моментов Т_к и углов закручивания вала φ.

Решение:

Угловая скорость вала согласно (3.3) равна

Вращающие моменты:

Из условия равновесия вала ∑ T_i = 0 находим Т₂:

Т₂+Т₁+Т₃+Т₄=0;

Т₂=Т₁-Т₃-Т₄=3460 –1150-770=1540 Н∙м

Мощность N₂ снимается с вала:

N₂ = Т₂ ω = 1540 26 = 40000 Вт = 40 кВт.

Строим эпюру крутящих моментов – эТ_к

Сделаем сечение I – I в любом месте первого участка и из условия равновесия левой от сечения части получим значение

Уравнение равновесия Т₂+ = 0,

откуда = -T₂= - 1540 Н∙м

Момент считаем отрицательным в соответствии с принятым правилом знаков. Сделав сечение II – II на втором участке, из условия равновесия левой части получим: Т₂+Т₁+= 0,

откуда =Т₁ –Т₂ = 3460 – 1540 = 1920 Н∙м

Аналогично проведя сечение III – III на третьем участке, составляя уравнение равновесия для отсеченной левой части, получим момент

Т₂ +Т₁ +Т₃ += 0

=Т₁ –Т₂ -Т₃ = 3460 – 1540 – 1150 = 770 Н∙м

Таким образом, крутящий момент в любом сечении вала равен алгебраической сумме внешних моментов, расположенных по одну сторону от этого сечения. Величину крутящего момента на различных участках вала изображают графически, построив эпюры крутящих моментов. Для этого от оси абсцисс, располагаемой под схемой вала (рис. 3.1) откладываем ординаты, изображающие в выбранном масштабе величину крутящего момента на каждом участке с учетом его знака (положительные – вверх). Так как величина Т_к в пределах участка не зависит от положения сечения, эпюра Т_к имеет форму трех прямоугольников (рис. 3.1). Отметим, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного здесь внешнего сосредоточенного момента.

Z

l₀= 0,5 M l₁ = 2 M l₂ =1 M l₃ =1 M l₄ =0,5 M

Т₂ 1 Т₁ 2 Т₃ 3 Т₄

1 2 3

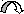
1920

770

ЭТ_k ,Н·М

-1540

A B C D E

эφ,град

К 0,334 L 0,125 M 0,041 N

Рис. 3.1

Условие прочности при кручении имеет вид

,

откуда

Принимаем d=70 мм.

Вычисление углов закручивания имеет серьезное практическое значение: оно необходимо для проверки жесткости вала. Практикой выбраны допустимые пределы для угла φ, которые нельзя превышать, чтобы не допустить нарушения в работе машины.

Эти пределы таковы: [φ] = 0,3° на метр длины вала ; при переменных нагрузках [φ] = 0,25°; для ударных нагрузок [φ] = 0,15°.

Из условия жесткости

,

В качестве окончательного значения принимаем d = 90 мм.

Пользуясь формулой (3.6) для определения деформаций, определим угловые перемещения сечений стержня φ и построим эпюры этих перемещений. Поскольку вал не имеет неподвижных сечений (вал – вращающийся стержень), то для построения эпюры угловых перемещений примем какое либо сечение за условно неподвижное, например, сечение А в точке приложения момента Т_2.

Определим поворот сечения В по отношения к сечению А – φ_ва:

Примем следующее правило знаков для углов поворота сечений: углы φ – положительны, когда сечение поворачивается (если смотреть вдоль оси справа налево) против часовой стрелки. В данном случае φ_ва будет отрицательным. В принятом масштабе отложим ординату φ_ва (рисунок 3.1).

Полученную точку К соединяем с точкой А , так как в пределах участка углы изменяются по законам прямой линии ( формула 3.6), в которую абсцисса сечения С входит в первой степени.

Вычислим теперь угол поворота сечения С по отношению к сечению В. Учитывая принятое правило знаков для углов закручивания, получаем

Угол поворота сечения С относительно сечения А равен

,

так как ,(отметим, что суммарное значение угла φ может получиться положительным, отрицательным и в частном случае равным нулю). Полученную величину в принятом масштабе откладываем вниз от оси опоры, получим точку L . соединяем точку L с точкой К, далее аналогично определяем угол поворота сечения D относительно С :

Аналогично выполненным ранее вычислениям угол поворота сечения D относительно А равен

Отложив эту величину в принятом масштабе вниз, получим точку М. Соединяя М с L , получим эпюру φ на участке DС . На участке DE скручивания не происходит, так как крутящий момент на этом участке равен нулю, поэтому там все сечения поворачиваются на столько же, на сколько поворачивается и сечение D. Участок МN эпюры φ здесь горизонтален.

Полный угол закручивания между концевыми сечениями равен алгебраической сумме углов закручивания для всех участков: